List of matrices - AbsoluteAstronomy.com

This page lists some important classes of matrices

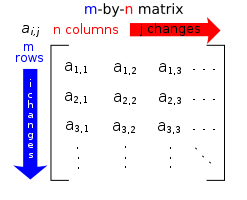
Matrix (mathematics)

In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...

used in mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, science

Science

Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...

and engineering

Engineering

Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...

. A matrix (plural matrices, or less commonly matrixes) is a rectangular array of number

Number

A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....

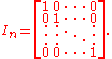
s called entries, as shown at the right. Matrices have a long history of both study and application, leading to diverse ways of classifying matrices. A first group is matrices satisfying concrete conditions of the entries, including constant matrices. An important example is the identity matrix

Identity matrix

In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...

given by

Further ways of classifying matrices are according to their eigenvalues or by imposing conditions on the product of the matrix with other matrices. Finally, many domains, both in mathematics and other sciences including physics

Physics

Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...

and chemistry

Chemistry

Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....

have particular matrices that are applied chiefly in these areas.

Matrices with explicitly constrained entries

The following lists matrices whose entries are subject to certain conditions. Many of them apply to square matrices only, that is matrices with the same number of columns and rows. The main diagonal of a square matrix is the diagonal

Diagonal

A diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a...

joining the upper left corner and the lower right one or equivalently the entries a_i,i. The other diagonal is called anti-diagonal (or counter-diagonal).

Name	Explanation	Notes, References
(0,1)-matrix	A matrix with all elements either 0 or 1.	Synonym for binary matrix, Boolean matrix and logical matrix.
Alternant matrix Alternant matrix In linear algebra, an alternant matrix, is a matrix with a particular structure, in which successive columns have a particular function applied to their entries. An alternant determinant is the determinant of an alternant matrix...	A matrix in which successive columns have a particular function applied to their entries.
Anti-diagonal matrix Anti-diagonal matrix In mathematics, an anti-diagonal matrix is a matrix where all the entries are zero except those on the diagonal going from the lower left corner to the upper right corner , known as the anti-diagonal....	A square matrix with all entries off the anti-diagonal equal to zero.
Anti-Hermitian matrix		Synonym for skew-Hermitian matrix.
Anti-symmetric matrix		Synonym for skew-symmetric matrix.
Arrowhead matrix Arrowhead matrix In the mathematical field of linear algebra, an arrowhead matrix is a square matrix containing zeros in all entries except for the first row, first column, and main diagonal...	A square matrix containing zeros in all entries except for the first row, first column, and main diagonal.
Band matrix Band matrix In mathematics, particularly matrix theory, a band matrix is a sparse matrix whose non-zero entries are confined to a diagonal band, comprising the main diagonal and zero or more diagonals on either side.-Matrix bandwidth:...	A square matrix whose non-zero entries are confined to a diagonal band.
Bidiagonal matrix Bidiagonal matrix A bidiagonal matrix is a matrix with non-zero entries along the main diagonal and either the diagonal above or the diagonal below.So that means there are two non zero diagonal in the matrix....	A matrix with elements only on the main diagonal and either the superdiagonal or subdiagonal.	Sometimes defined differently, see article.
Binary matrix	A matrix whose entries are all either 0 or 1.	Synonym for (0,1)-matrix, Boolean matrix or logical matrix.
Bisymmetric matrix	A square matrix that is symmetric with respect to its main diagonal and its main cross-diagonal.
Block-diagonal matrix	A block matrix Block matrix In the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle... with entries only on the diagonal.
Block matrix Block matrix In the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...	A matrix partitioned in sub-matrices called blocks.
Block tridiagonal matrix	A block matrix which is essentially a tridiagonal matrix but with submatrices in place of scalar elements
Boolean matrix	A matrix whose entries are all either 0 or 1.	Synonym for (0,1)-matrix, binary matrix or logical matrix.
Cauchy matrix	A matrix whose elements are of the form 1/(x_i + y_j) for (x_i), (y_j) injective sequences (i.e., taking every value only once).
Centrosymmetric matrix Centrosymmetric matrix In mathematics, especially in linear algebra and matrix theory, a centrosymmetric matrix is a matrix which is symmetric about its center. More precisely, an n × n matrix A = [ Ai,j ] is centrosymmetric when its entries satisfy...	A matrix symmetric about its center; i.e., a_ij = a_{n−i+1,n−j+1}
Conference matrix Conference matrix In mathematics, a conference matrix is a square matrix C with 0 on the diagonal and +1 and −1 off the diagonal, such that CTC is a multiple of the identity matrix I...	A square matrix with zero diagonal and +1 and −1 off the diagonal, such that C^TC is a multiple of the identity matrix.
Complex Hadamard matrix	A matrix with all rows and columns mutually orthogonal, whose entries are unimodular.
Copositive matrix Copositive matrix In mathematics, specifically linear algebra, a real matrix A is copositive ifx^TAx\geq 0for every nonnegative vector x\geq 0. The collection of all copositive matrices is a proper cone; it includes as a subset the collection of real positive-definite matrices.Copositive matrices find applications...	A square matrix A with real coefficients, such that 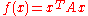is nonnegative for every nonnegative vector x
Diagonally dominant matrix Diagonally dominant matrix In mathematics, a matrix is said to be diagonally dominant if for every row of the matrix, the magnitude of the diagonal entry in a row is larger than or equal to the sum of the magnitudes of all the other entries in that row...	a_ii\| > Σ_j≠i \|a_ij\|.
Diagonal matrix Diagonal matrix In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...	A square matrix with all entries outside the main diagonal equal to zero.
Elementary matrix	A square matrix derived by applying an elementary row operation to the identity matrix.
Equivalent matrix	A matrix that can be derived from another matrix through a sequence of elementary row or column operations.
Frobenius matrix Frobenius matrix A Frobenius matrix is a special kind of square matrix from the branch of mathematics known as numerical mathematics. A matrix is a Frobenius matrix if it has the following three properties:* all entries on the main diagonal are ones...	A square matrix in the form of an identity matrix but with arbitrary entries in one column below the main diagonal.
Generalized permutation matrix Generalized permutation matrix In mathematics, a generalized permutation matrix is a matrix with the same nonzero pattern as a permutation matrix, i.e. there is exactly one nonzero entry in each row and each column. Unlike a permutation matrix, where the nonzero entry must be 1, in a generalized permutation matrix the nonzero...	A square matrix with precisely one nonzero element in each row and column.
Hadamard matrix Hadamard matrix In mathematics, an Hadamard matrix, named after the French mathematician Jacques Hadamard, is a square matrix whose entries are either +1 or −1 and whose rows are mutually orthogonal...	A square matrix with entries +1, −1 whose rows are mutually orthogonal.
Hankel matrix	A matrix with constant skew-diagonals; also an upside down Toeplitz matrix.	A square Hankel matrix is symmetric.
Hermitian matrix	A square matrix which is equal to its conjugate transpose Conjugate transpose In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry... , A = A^*.
Hessenberg matrix Hessenberg matrix In linear algebra, a Hessenberg matrix is a special kind of square matrix, one that is "almost" triangular. To be exact, an upper Hessenberg matrix has zero entries below the first subdiagonal, and a lower Hessenberg matrix has zero entries above the first superdiagonal...	An "almost" triangular matrix, for example, an upper Hessenberg matrix has zero entries below the first subdiagonal.
Hollow matrix Hollow matrix In mathematics, a hollow matrix may refer to one of several related classes of matrix.-Diagonal entries all zero:A hollow matrix may be a square matrix whose diagonal elements are all equal to zero...	A square matrix whose main diagonal comprises only zero elements.
Integer matrix Integer matrix In mathematics, an integer matrix is a matrix whose entries are all integers. Examples include binary matrices, the zero matrix, the unit matrix, and the adjacency matrices used in graph theory, amongst many others...	A matrix whose entries are all integers.
Logical matrix	A matrix with all entries either 0 or 1.	Synonym for (0,1)-matrix, binary matrix or Boolean matrix. Can be used to represent a k-adic relation Relation (mathematics) In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple... .
Metzler matrix	A matrix whose off-diagonal entries are non-negative.
Monomial matrix	A square matrix with exactly one non-zero entry in each row and column.	Synonym for generalized permutation matrix.
Moore matrix	A row consists of a, a^q, a^q², etc., and each row uses a different variable.
Nonnegative matrix Nonnegative matrix A nonnegative matrix is a matrix in which all the elements are equal to or greater than zeroA positive matrix is a matrix in which all the elements are greater than zero...	A matrix with all nonnegative entries.
Partitioned matrix	A matrix partitioned into sub-matrices, or equivalently, a matrix whose entries are themselves matrices rather than scalars	Synonym for block matrix
Parisi matrix	A block-hierarchical matrix. It consist of growing blocks placed along the diagonal, each block is itself a Parisi matrix of a smaller size.	In theory of spin-glasses is also known as a replica matrix.
Pentadiagonal matrix Pentadiagonal matrix In linear algebra, a pentadiagonal matrix is a matrix that is nearly diagonal; to be exact, it is a matrix in which the only nonzero entries are on the main diagonal, and the first two diagonals above and below it...	A matrix with the only nonzero entries on the main diagonal and the two diagonals just above and below the main one.
Permutation matrix Permutation matrix In mathematics, in matrix theory, a permutation matrix is a square binary matrix that has exactly one entry 1 in each row and each column and 0s elsewhere...	A matrix representation of a permutation Permutation In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order... , a square matrix with exactly one 1 in each row and column, and all other elements 0.
Persymmetric matrix Persymmetric matrix In mathematics, persymmetric matrix may refer to:# a square matrix which is symmetric in the northeast-to-southwest diagonal; or# a square matrix such that the values on each line perpendicular to the main diagonal are the same for a given line....	A matrix that is symmetric about its northeast-southwest diagonal, i.e., a_ij = a_{n−j+1,n−i+1}
Polynomial matrix Polynomial matrix A polynomial matrix or sometimes matrix polynomial is a matrix whose elements are univariate or multivariate polynomials. A λ-matrix is a matrix whose elements are polynomials in λ....	A matrix whose entries are polynomial Polynomial In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents... s.
Positive matrix	A matrix with all positive entries.
Quaternionic matrix Quaternionic matrix A quaternionic matrix is a matrix whose elements are quaternions.-Matrix operations:The quaternions form a noncommutative ring, and therefore addition and multiplication can be defined for quaternionic matrices as for matrices over any ring.Addition...	A matrix whose entries are quaternion Quaternion In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space... s.
Sign matrix	A matrix whose entries are either +1, 0, or −1.
Signature matrix	A diagonal matrix where the diagonal elements are either +1 or −1.
Skew-Hermitian matrix Skew-Hermitian matrix In linear algebra, a square matrix with complex entries is said to be skew-Hermitian or antihermitian if its conjugate transpose is equal to its negative. That is, the matrix A is skew-Hermitian if it satisfies the relationA^\dagger = -A,\;...	A square matrix which is equal to the negative of its conjugate transpose Conjugate transpose In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry... , A^* = −A.
Skew-symmetric matrix Skew-symmetric matrix In mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...	A matrix which is equal to the negative of its transpose Transpose In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:... , A^T = −A.
Skyline matrix Skyline matrix A skyline matrix, or a variable band matrix, or envelope storage scheme is a form of a sparse matrix storage format matrix that reduces the storage requirement of a matrix more than banded storage. In banded storage, all entries within a fixed distance from the diagonal are stored...	A rearrangement of the entries of a banded matrix which requires less space.
Sparse matrix Sparse matrix In the subfield of numerical analysis, a sparse matrix is a matrix populated primarily with zeros . The term itself was coined by Harry M. Markowitz....	A matrix with relatively few non-zero elements.	Sparse matrix algorithms can tackle huge sparse matrices that are utterly impractical for dense matrix algorithms.
Sylvester matrix Sylvester matrix In mathematics, a Sylvester matrix is a matrix associated to two polynomials that provides information about those polynomials. It is named for James Joseph Sylvester.-Definition:...	A square matrix whose entries come from coefficients of two polynomials.	The Sylvester matrix is nonsingular if and only if the two polynomials are coprime Coprime In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1... to each other.
Symmetric matrix	A square matrix which is equal to its transpose Transpose In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:... , A = A^T (a_i,j = a_j,i).
Toeplitz matrix Toeplitz matrix In linear algebra, a Toeplitz matrix or diagonal-constant matrix, named after Otto Toeplitz, is a matrix in which each descending diagonal from left to right is constant...	A matrix with constant diagonals.
Triangular matrix Triangular matrix In the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...	A matrix with all entries above the main diagonal equal to zero (lower triangular) or with all entries below the main diagonal equal to zero (upper triangular).
Tridiagonal matrix	A matrix with the only nonzero entries on the main diagonal and the diagonals just above and below the main one.
Unitary matrix	A square matrix whose inverse is equal to its conjugate transpose Conjugate transpose In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry... , A⁻¹ = A^*.
Vandermonde matrix	A row consists of 1, a, a², a³, etc., and each row uses a different variable.
Walsh matrix Walsh matrix In mathematics, a Walsh matrix is a specific square matrix, with dimensions a power of 2, the entries of which are +1 or −1, and the property that the dot product of any two distinct rows is zero. The Walsh matrix was proposed by Joseph Leonard Walsh in 1923...	A square matrix, with dimensions a power of 2, the entries of which are +1 or -1.
Z-matrix	A matrix with all off-diagonal entries less than zero.

Constant matrices

The list below comprises matrices whose elements are constant for any given dimension (size) of matrix. The matrix entries will be denoted a_ij. The table below uses the Kronecker delta δ_ij for two integers i and j which is 1 if i = j and 0 else.

Name	Explanation	Symbolic description of the entries	Notes
Exchange matrix Exchange matrix In mathematics, especially linear algebra, the exchange matrix is a special case of a permutation matrix, where the 1 elements reside on the counterdiagonal and all other elements are zero...	A binary matrix with ones on the anti-diagonal, and zeroes everywhere else.	a_ij = δ_{n + 1 − i,j}	A permutation matrix Permutation matrix In mathematics, in matrix theory, a permutation matrix is a square binary matrix that has exactly one entry 1 in each row and each column and 0s elsewhere... .
Hilbert matrix		a_ij = (i + j − 1)⁻¹.	A Hankel matrix.
Identity matrix Identity matrix In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...	A square diagonal matrix, with all entries on the main diagonal equal to 1, and the rest 0	a_ij = δ_ij
Lehmer matrix		a_ij = min(i,j) ÷ max(i,j).	A positive symmetric matrix.
Matrix of ones	A matrix with all entries equal to one	a_ij = 1.
Pascal matrix Pascal matrix In mathematics, particularly matrix theory and combinatorics, the Pascal matrix is an infinite matrix containing the binomial coefficients as its elements. There are three ways to achieve this: as either an upper-triangular matrix, a lower-triangular matrix, or a symmetric matrix...	A matrix containing the entries of Pascal's triangle Pascal's triangle In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal... .
Pauli matrices Pauli matrices The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...	A set of three 2 × 2 complex Hermitian and unitary matrices. When combined with the I₂ identity matrix, they form an orthogonal basis for the 2 × 2 complex Hermitian matrices.
Redheffer matrix Redheffer matrix In mathematics, a Redheffer matrix, studied by , is a matrix whose entries aij are 1 if i divides j or if j = 1; otherwise, aij = 0....		a_ij are 1 if i divides j or if j = 1; otherwise, a_ij = 0.	A (0, 1)-matrix.
Shift matrix Shift matrix In mathematics, a shift matrix is a binary matrix with ones only on the superdiagonal or subdiagonal, and zeroes elsewhere. A shift matrix U with ones on the superdiagonal is an upper shift matrix....	A matrix with ones on the superdiagonal or subdiagonal and zeroes elsewhere.	a_ij = δ_i+1,j or a_ij = δ_i−1,j	Multiplication by it shifts matrix elements by one position.
Zero matrix	A matrix with all entries equal to zero.	a_ij = 0.

Matrices with conditions on eigenvalues or eigenvectors

Name	Explanation	Notes
Companion matrix	A matrix whose eigenvalues are equal to the roots of the polynomial.
Defective matrix Defective matrix In linear algebra, a defective matrix is a square matrix that does not have a complete basis of eigenvectors, and is therefore not diagonalizable. In particular, an n × n matrix is defective if and only if it does not have n linearly independent eigenvectors...	A square matrix that does not have a complete basis of eigenvectors, and is thus not diagonalisable.
Diagonalizable matrix Diagonalizable matrix In linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...	A square matrix similar to a diagonal matrix.	It has an eigenbasis, that is, a complete set of linearly independent eigenvectors.
Hurwitz matrix Hurwitz matrix -Hurwitz matrix and the Hurwitz stability criterion:In mathematics, Hurwitz matrix is a structured real square matrix constructed with coefficientsof a real polynomial...	A matrix whose eigenvalues have strictly negative real part. A stable system of differential equations may be represented by a Hurwitz matrix.
Positive-definite matrix Positive-definite matrix In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....	A Hermitian matrix with every eigenvalue positive.
Stability matrix		Synonym for Hurwitz matrix Hurwitz matrix -Hurwitz matrix and the Hurwitz stability criterion:In mathematics, Hurwitz matrix is a structured real square matrix constructed with coefficientsof a real polynomial... .
Stieltjes matrix Stieltjes matrix In mathematics, particularly matrix theory, a Stieltjes matrix, named after Thomas Joannes Stieltjes, is a real symmetric positive definite matrix with nonpositive off-diagonal entries. A Stieltjes matrix is necessarily an M-matrix...	A real symmetric positive definite matrix with nonpositive off-diagonal entries.	Special case of an M-matrix M-matrix In mathematics, especially linear algebra, an M-matrix is a Z-matrix with eigenvalues whose real parts are positive. M-matrices are a subset of the class of P-matrices, and also of the class of inverse-positive matrices In mathematics, especially linear algebra, an M-matrix is a Z-matrix with... .

Matrices satisfying conditions on products or inverses

A number of matrix-related notions is about properties of products or inverses of the given matrix. The matrix product of a m-by-n matrix A and a n-by-k matrix B is the m-by-k matrix C given by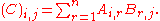

This matrix product is denoted AB. Unlike the product of numbers, matrix products are not commutative, that is to say AB need not be equal to BA. A number of notions are concerned with the failure of this commutativity. An inverse of square matrix A is a matrix B (necessarily of the same dimension as A) such that AB = I. Equivalently, BA = I. An inverse need not exist. If it exists, B is uniquely determined, and is also called the inverse of A, denoted A⁻¹.

Name	Explanation	Notes
Congruent matrix Matrix congruence In mathematics, two matrices A and B over a field are called congruent if there exists an invertible matrix P over the same field such thatwhere "T" denotes the matrix transpose...	Two matrices A and B are congruent if there exists an invertible matrix P such that P^T A P = B.	Compare with similar matrices.
Idempotent matrix Idempotent matrix In algebra, an idempotent matrix is a matrix which, when multiplied by itself, yields itself. That is, the matrix M is idempotent if and only if MM = M...	A matrix that has the property A² = AA = A.
Invertible matrix	A square matrix having a multiplicative inverse, that is, a matrix B such that AB = BA = I.	Invertible matrices form the general linear group General linear group In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible... .
Involutary matrix	A square matrix which is its own inverse, i.e., AA = I.	Signature matrices have this property.
Nilpotent matrix Nilpotent matrix In linear algebra, a nilpotent matrix is a square matrix N such thatN^k = 0\,for some positive integer k. The smallest such k is sometimes called the degree of N....	A square matrix satisfying A^q = 0 for some positive integer q.	Equivalently, the only eigenvalue of A is 0.
Normal matrix Normal matrix A complex square matrix A is a normal matrix ifA^A=AA^ \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT...	A square matrix that commutes with its conjugate transpose Conjugate transpose In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry... : AA^∗ = A^∗A	They are the matrices to which the spectral theorem Spectral theorem In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized... applies.
Orthogonal matrix Orthogonal matrix In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....	A matrix whose inverse is equal to its transpose Transpose In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:... , A⁻¹ = A^T.	They form the orthogonal group Orthogonal group In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication... .
Orthonormal matrix	A matrix whose columns are orthonormal vectors.
Similar matrix	Two matrices A and B are similar if there exists an invertible matrix P such that P⁻¹AP = B.	Compare with congruent matrices.
Singular matrix	A square matrix that is not invertible.
Unimodular matrix Unimodular matrix In mathematics, a unimodular matrix M is a square integer matrix with determinant +1 or −1. Equivalently, it is an integer matrix that is invertible over the integers: there is an integer matrix N which is its inverse...	An invertible matrix with entries in the integers (integer matrix Integer matrix In mathematics, an integer matrix is a matrix whose entries are all integers. Examples include binary matrices, the zero matrix, the unit matrix, and the adjacency matrices used in graph theory, amongst many others... )	Necessarily the determinant is +1 or −1.
Unipotent matrix	A square matrix with all eigenvalues equal to 1.	Equivalently, is nilpotent. See also unipotent group.
Totally unimodular matrix	A matrix for which every non-singular square submatrix is unimodular Unimodular matrix In mathematics, a unimodular matrix M is a square integer matrix with determinant +1 or −1. Equivalently, it is an integer matrix that is invertible over the integers: there is an integer matrix N which is its inverse... . This has some implications in the linear programming Linear programming Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships... relaxation of an integer program.
Weighing matrix	A square matrix the entries of which are in }, such that AA^T = wI for some positive integer w.

Matrices with specific applications

Name	Explanation	Used in	Notes
Adjugate matrix Adjugate matrix In linear algebra, the adjugate or classical adjoint of a square matrix is a matrix that plays a role similar to the inverse of a matrix; it can however be defined for any square matrix without the need to perform any divisions....	The matrix containing minors Minor (linear algebra) In linear algebra, a minor of a matrix A is the determinant of some smaller square matrix, cut down from A by removing one or more of its rows or columns... of a given square matrix.	Calculating inverse matrices via Laplace's formula.
Alternating sign matrix Alternating sign matrix In mathematics, an alternating sign matrix is a square matrix of 0s, 1s, and −1s such that the sum of each row and column is 1 and the nonzero entries in each row and column alternate in sign. These matrices arise naturally when using Dodgson condensation to compute a determinant...	A square matrix of with entries 0, 1 and −1 such that the sum of each row and column is 1 and the nonzero entries in each row and column alternate in sign.	Dodgson condensation Dodgson condensation In mathematics, Dodgson condensation is a method of computing the determinants of square matrices. It is named for its inventor Charles Dodgson... to calculate determinants
Augmented matrix Augmented matrix In linear algebra, an augmented matrix is a matrix obtained by appending the columns of two given matrices, usually for the purpose of performing the same elementary row operations on each of the given matrices.Given the matrices A and B, where:A =...	A matrix whose rows are concatenations of the rows of two smaller matrices.	Calculating inverse matrices.
Bézout matrix Bézout matrix In mathematics, a Bézout matrix is a special square matrix associated with two polynomials. Such matrices are sometimes used to test the stability of a given polynomial.-Definition:...	A square matrix which may be used as a tool for the efficient location of polynomial zeros	Control theory Control theory Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference... , Stable polynomial Stable polynomial A polynomial is said to be stable if either:* all its roots lie in the open left half-plane, or* all its roots lie in the open unit disk.The first condition defines Hurwitz stability and the second one Schur stability. Stable polynomials arise in various mathematical fields, for example in... s
Carleman matrix Carleman matrix In mathematics, a Carleman matrix is a matrix that is used to convert function composition into matrix multiplication. They are used in iteration theory to find the continuous iteration of functions that cannot be iterated by pattern recognition alone...	A matrix that converts composition of functions to multiplication of matrices.
Cartan matrix Cartan matrix In mathematics, the term Cartan matrix has three meanings. All of these are named after the French mathematician Élie Cartan. In fact, Cartan matrices in the context of Lie algebras were first investigated by Wilhelm Killing, whereas the Killing form is due to Cartan.- Lie algebras :A generalized...	A matrix associated with a finite-dimensional associative algebra Associative algebra In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R... , or a semisimple Lie algebra (the two meanings are distinct).
Circulant matrix Circulant matrix In linear algebra, a circulant matrix is a special kind of Toeplitz matrix where each row vector is rotated one element to the right relative to the preceding row vector. In numerical analysis, circulant matrices are important because they are diagonalized by a discrete Fourier transform, and hence...	A matrix where each row is a circular shift of its predecessor.	System of linear equations, discrete Fourier transform Discrete Fourier transform In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
Cofactor matrix	A containing the cofactors Cofactor (linear algebra) In linear algebra, the cofactor describes a particular construction that is useful for calculating both the determinant and inverse of square matrices... , i.e., signed minors Minor (linear algebra) In linear algebra, a minor of a matrix A is the determinant of some smaller square matrix, cut down from A by removing one or more of its rows or columns... , of a given matrix.
Commutation matrix Commutation matrix In mathematics, especially in linear algebra and matrix theory, the commutation matrix is used for transforming the vectorized form of a matrix into the vectorized form of its transpose...	A matrix used for transforming the vectorized form of a matrix into the vectorized form of its transpose.
Coxeter matrix	A matrix related to Coxeter groups, which describe symmetries Symmetry Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection... in a structure or system.
Distance matrix Distance matrix In mathematics, computer science and graph theory, a distance matrix is a matrix containing the distances, taken pairwise, of a set of points...	A square matrix containing the distances, taken pairwise, of a set of points Point (geometry) In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics... .	Computer vision Computer vision Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions... , network analysis Network analysis Network analysis can refer to:* Analysis of general networks: see Network theory.* Electrical network analysis see Network analysis .* Social network analysis.You may also be interested in Network planning and design... .	See also Euclidean distance matrix.
Duplication matrix Duplication matrix In mathematics, especially in linear algebra and matrix theory, the duplication matrix and the elimination matrix are linear transformations used for transforming half-vectorizations of matrices into vectorizations or vice-versa....	A linear transformation matrix used for transforming half-vectorizations of matrices into vectorization Vectorization (mathematics) In mathematics, especially in linear algebra and matrix theory, the vectorization of a matrix is a linear transformation which converts the matrix into a column vector... s.
Elimination matrix	A linear transformation matrix used for transforming vectorization Vectorization (mathematics) In mathematics, especially in linear algebra and matrix theory, the vectorization of a matrix is a linear transformation which converts the matrix into a column vector... s of matrices into half-vectorizations.
Euclidean distance matrix	A matrix that describes the pairwise distances between points Point (geometry) In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics... in Euclidean space Euclidean space In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions... .		See also distance matrix Distance matrix In mathematics, computer science and graph theory, a distance matrix is a matrix containing the distances, taken pairwise, of a set of points... .
Fundamental matrix (linear differential equation)	A matrix containing the fundamental solutions of a linear ordinary differential equation Ordinary differential equation In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable.... .
Generator matrix Generator matrix In coding theory, a generator matrix is a basis for a linear code, generating all its possible codewords.If the matrix is G and the linear code is C,where w is a codeword of the linear code C, c is a row vector, and a bijection exists between w and c. A generator matrix for an q-code has...	A matrix whose rows generate all elements of a linear code Linear code In coding theory, a linear code is an error-correcting code for which any linear combination of codewords is also a codeword. Linear codes are traditionally partitioned into block codes and convolutional codes, although Turbo codes can be seen as a hybrid of these two types. Linear codes allow for... .	Coding theory Coding theory Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
Gramian matrix	A matrix containing the pairwise angles of given vectors in an inner product space Inner product space In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors... .	Test linear independence Linear independence In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent... of vectors, including ones in function space Function space In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:... s.	They are real symmetric.
Hessian matrix Hessian matrix In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...	A square matrix of second partial derivatives Partial derivative In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant... of a scalar-valued function.	Detecting local minima and maxima of scalar-valued functions in several variables; Blob detection Blob detection In the area of computer vision, blob detection refers to visual modules that are aimed at detecting points and/or regions in the image that differ in properties like brightness or color compared to the surrounding... (computer vision Computer vision Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions... )
Householder matrix Householder transformation In linear algebra, a Householder transformation is a linear transformation that describes a reflection about a plane or hyperplane containing the origin. Householder transformations are widely used in numerical linear algebra, to perform QR decompositions and in the first step of the QR algorithm...	A transformation matrix widely used in matrix algorithms.	QR decomposition QR decomposition In linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A=QR of an orthogonal matrix Q and an upper triangular matrix R... .
Jacobian matrix	A matrix of first-order partial derivatives of a vector-valued function.	Implicit function theorem Implicit function theorem In multivariable calculus, the implicit function theorem is a tool which allows relations to be converted to functions. It does this by representing the relation as the graph of a function. There may not be a single function whose graph is the entire relation, but there may be such a function on... ; Smooth morphisms (algebraic geometry Algebraic geometry Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex... ).
Payoff matrix	A matrix in game theory Game theory Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others... and economics Economics Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"... , that represents the payoffs in a normal form game Normal form game In game theory, normal form is a way of describing a game. Unlike extensive form, normal-form representations are not graphical per se, but rather represent the game by way of a matrix. While this approach can be of greater use in identifying strictly dominated strategies and Nash equilibria, some... where players move simultaneously
Pick matrix	A matrix that occurs in the study of analytical interpolation problems.
Random matrix Random matrix In probability theory and mathematical physics, a random matrix is a matrix-valued random variable. Many important properties of physical systems can be represented mathematically as matrix problems...	A matrix whose entries consist of random numbers from some specified random distribution.
Rotation matrix	A matrix representing a rotational geometric transformation.	Special orthogonal group, Euler angles
Seifert matrix	A matrix in knot theory Knot theory In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a... , primarily for the algebraic analysis of topological properties of knots and links.	Alexander polynomial Alexander polynomial In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923...
Shear matrix Shear matrix In mathematics, a shear matrix or transvection is an elementary matrix that represents the addition of a multiple of one row or column to another...	An elementary matrix whose corresponding geometric transformation is a shear transformation.
Similarity matrix Similarity matrix A similarity matrix is a matrix of scores which express the similarity between two data points. Similarity matrices are strongly related to their counterparts, distance matrices and substitution matrices.-Use in sequence alignment:...	A matrix of scores which express the similarity between two data points.	Sequence alignment Sequence alignment In bioinformatics, a sequence alignment is a way of arranging the sequences of DNA, RNA, or protein to identify regions of similarity that may be a consequence of functional, structural, or evolutionary relationships between the sequences. Aligned sequences of nucleotide or amino acid residues are...
Symplectic matrix	A square matrix preserving a standard skew-symmetric form.	Symplectic group Symplectic group In mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually... , symplectic manifold Symplectic manifold In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology... .
Totally positive matrix Totally positive matrix In mathematics, a totally positive matrix is a matrix in which the determinant of every square submatrix is positive. For example, a Vandermonde matrix whose nodes are positive and increasing is a totally positive matrix....	A matrix with determinant Determinant In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well... s of all its square submatrices positive.	Generating the reference points of Bézier curve Bézier curve A Bézier curve is a parametric curve frequently used in computer graphics and related fields. Generalizations of Bézier curves to higher dimensions are called Bézier surfaces, of which the Bézier triangle is a special case.... in computer graphics Computer graphics Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware.... .
Transformation matrix	A matrix representing a linear transformation Linear transformation In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0... , often from one co-ordinate space to another to facilitate a geometric transform or projection.

Derogatory matrix — a square n×n matrix whose minimal polynomial is of order less than n.
Moment matrix
Moment matrix
In mathematics, a moment matrix is a special symmetric square matrix whose rows and columns are indexed by monomials. The entries of the matrix depend on the product of the indexing monomials only...

— a symmetric matrix whose elements are the products of common row/column index dependent monomials.
X-Y-Z matrix — a generalisation of the (rectangular) matrix to a cuboidal form (a 3-dimensional array of entries).

Matrices used in statistics

The following matrices find their main application in statistics

Statistics

Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....

and probability theory

Probability theory

Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...

Bernoulli matrix — a square matrix with entries +1, −1, with equal probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...

of each.
Centering matrix
Centering matrix
In mathematics and multivariate statistics, the centering matrix is a symmetric and idempotent matrix, which when multiplied with a vector has the same effect as subtracting the mean of the components of the vector from every component.- Definition :...

— a matrix which, when multiplied with a vector, has the same effect as subtracting the mean of the components of the vector from every component.
Correlation matrix — a symmetric n×n matrix, formed by the pairwise correlation coefficients of several random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...

s.
Covariance matrix
Covariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...

— a symmetric n×n matrix, formed by the pairwise covariance
Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...

s of several random variables. Sometimes called a dispersion matrix.
Dispersion matrix — another name for a covariance matrix.
Doubly stochastic matrix
Doubly stochastic matrix
In mathematics, especially in probability and combinatorics, a doubly stochastic matrix,is a square matrix of nonnegative real numbers, each of whose rows and columns sums to 1...

— a non-negative matrix such that each row and each column sums to 1 (thus the matrix is both left stochastic and right stochastic)
Fisher information matrix — a matrix representing the variance of the partial derivative, with respect to a parameter, of the log of the likelihood function of a random variable.
Hat matrix
Hat matrix
In statistics, the hat matrix, H, maps the vector of observed values to the vector of fitted values. It describes the influence each observed value has on each fitted value...

- a square matrix used in statistics to relate fitted values to observed values.
Precision matrix — a symmetric n×n matrix, formed by inverting the covariance matrix. Also called the information matrix.
Stochastic matrix
Stochastic matrix
In mathematics, a stochastic matrix is a matrix used to describe the transitions of a Markov chain. It has found use in probability theory, statistics and linear algebra, as well as computer science...

— a non-negative matrix describing a stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...

. The sum of entries of any row is one.
Transition matrix — a matrix representing the probabilities of conditions changing from one state to another in a Markov chain
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...

Matrices used in graph theory

The following matrices find their main application in graph

Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

and network theory

Network theory

Network theory is an area of computer science and network science and part of graph theory. It has application in many disciplines including statistical physics, particle physics, computer science, biology, economics, operations research, and sociology...

Adjacency matrix
Adjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...

— a square matrix representing a graph, with a_ij non-zero if vertex i and vertex j are adjacent.
Biadjacency matrix — a special class of adjacency matrix
Adjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...

that describes adjacency in bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...

s.
Degree matrix
Degree matrix
In the mathematical field of graph theory the degree matrix is a diagonal matrix which contains information about the degree of each vertex. It is used together with the adjacency matrix to construct the Laplacian matrix of a graph.-Definition:...

— a diagonal matrix defining the degree of each vertex
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...

in a graph.
Edmonds matrix — a square matrix of a bipartite graph.
Incidence matrix
Incidence matrix
In mathematics, an incidence matrix is a matrix that shows the relationship between two classes of objects. If the first class is X and the second is Y, the matrix has one row for each element of X and one column for each element of Y. The entry in row x and column y is 1 if x and y are related ...

— a matrix representing a relationship between two classes of objects (usually vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...

and edges in the context of graph theory).
Laplacian matrix
Laplacian matrix
In the mathematical field of graph theory the Laplacian matrix, sometimes called admittance matrix or Kirchhoff matrix, is a matrix representation of a graph. Together with Kirchhoff's theorem it can be used to calculate the number of spanning trees for a given graph. The Laplacian matrix can be...

— a matrix equal to the degree matrix minus the adjacency matrix for a graph, used to find the number of spanning trees in the graph.
Seidel adjacency matrix
Seidel adjacency matrix
In mathematics, in graph theory, the Seidel adjacency matrix of a simple graph G is the symmetric matrix with a row and column for each vertex, having 0 on the diagonal and, in the positions corresponding to vertices vi and vj, −1 if the vertices are adjacent...

— a matrix similar to the usual adjacency matrix
Adjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...

but with −1 for adjacency; +1 for nonadjacency; 0 on the diagonal.
Tutte matrix
Tutte matrix
In graph theory, the Tutte matrix A of a graph G = is a matrix used to determine the existence of a perfect matching: that is, a set of edges which is incident with each vertex exactly once....

— a generalisation of the Edmonds matrix for a balanced bipartite graph.

Matrices used in science and engineering

Cabibbo-Kobayashi-Maskawa matrix
Cabibbo-Kobayashi-Maskawa matrix
In the Standard Model of particle physics, the Cabibbo–Kobayashi–Maskawa matrix is a unitary matrix which contains information on the strength of flavour-changing weak decays...

— a unitary matrix used in particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...

to describe the strength of flavour-changing weak decays.
Density matrix
Density matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...

— a matrix describing the statistical state of a quantum system. Hermitian, non-negative and with trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...

1.
Fundamental matrix (computer vision) — a 3 × 3 matrix in computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...

that relates corresponding points in stereo images.
Fuzzy associative matrix
Fuzzy associative matrix
A fuzzy associative matrix expresses fuzzy logic rules in tabular form. These rules usually take two variables as input, mapping cleanly to a two-dimensional matrix, although theoretically a matrix of any number of dimensions is possible....

— a matrix in artificial intelligence
Artificial intelligence
Artificial intelligence is the intelligence of machines and the branch of computer science that aims to create it. AI textbooks define the field as "the study and design of intelligent agents" where an intelligent agent is a system that perceives its environment and takes actions that maximize its...

, used in machine learning processes.
Gamma matrices — 4 × 4 matrices in quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...

.
Gell-Mann matrices
Gell-Mann matrices
The Gell-Mann matrices, named for Murray Gell-Mann, are one possible representation of the infinitesimal generators of the special unitary group called SU....

— a generalisation of the Pauli matrices
Pauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...

, these matrices are one notable representation of the infinitesimal generators of the special unitary group
Special unitary group
The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...

, SU(3).
Hamiltonian matrix — a matrix used in a variety of fields, including quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...

and linear quadratic regulator (LQR) systems.
Irregular matrix
Irregular matrix
An irregular matrix, or ragged matrix, can be described as a matrix that has a different number of elements in each row. Ragged matrices are not used in linear algebra, since standard matrix transformations cannot be performed on them, but they are useful as arrays in computing...

— a matrix used in computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...

which has a varying number of elements in each row.
Overlap matrix
Overlap matrix
The overlap matrix is a square matrix, used in quantum chemistry to describe the inter-relationship of a set of basis vectors of a quantum system. In particular, if the vectors are orthogonal to one another, the overlap matrix will be diagonal. In addition, if the basis vectors form an...

— a type of Gramian matrix, used in quantum chemistry
Quantum chemistry
Quantum chemistry is a branch of chemistry whose primary focus is the application of quantum mechanics in physical models and experiments of chemical systems...

to describe the inter-relationship of a set of basis vectors of a quantum
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...

system.
S matrix
S matrix
In physics, the scattering matrix relates the initial state and the final state of a physical system undergoing a scattering process...

— a matrix in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...

that connects asymptotic (infinite past and future) particle states.
State transition matrix
State-transition matrix
In control theory, the state-transition matrix is a matrix whose product with the state vector x at an initial time t_0 gives x at a later time t. The state-transition matrix can be used to obtain the general solution of linear dynamical systems...

— Exponent of state matrix in control systems.
Substitution matrix
Substitution matrix
In bioinformatics and evolutionary biology, a substitution matrix describes the rate at which one character in a sequence changes to other character states over time...

— a matrix from bioinformatics
Bioinformatics
Bioinformatics is the application of computer science and information technology to the field of biology and medicine. Bioinformatics deals with algorithms, databases and information systems, web technologies, artificial intelligence and soft computing, information and computation theory, software...

, which describes mutation rates of amino acid
Amino acid
Amino acids are molecules containing an amine group, a carboxylic acid group and a side-chain that varies between different amino acids. The key elements of an amino acid are carbon, hydrogen, oxygen, and nitrogen...

or DNA
DNA
Deoxyribonucleic acid is a nucleic acid that contains the genetic instructions used in the development and functioning of all known living organisms . The DNA segments that carry this genetic information are called genes, but other DNA sequences have structural purposes, or are involved in...

sequences.
Z-matrix
Z-matrix (chemistry)
In chemistry, the Z-matrix is a way to represent a system built of atoms. A Z-matrix is also known as an internal coordinate representation...

— a matrix in chemistry
Chemistry
Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....

, representing a molecule in terms of its relative atomic geometry.

Other matrix-related terms and definitions

Jordan canonical form — an 'almost' diagonalised matrix, where the only non-zero elements appear on the lead and super-diagonals.
Linear independence
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...

— two or more vectors
Coordinate vector
In linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....

are linearly independent if there is no way to construct one from linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...

s of the others.
Matrix exponential
Matrix exponential
In mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. Abstractly, the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group....

— defined by the exponential series.
Matrix representation of conic sections
Pseudoinverse
Pseudoinverse
In mathematics, and in particular linear algebra, a pseudoinverse of a matrix is a generalization of the inverse matrix. The most widely known type of matrix pseudoinverse is the Moore–Penrose pseudoinverse, which was independently described by E. H. Moore in 1920, Arne Bjerhammar in 1951 and...

— a generalization of the inverse matrix.
Quaternionic matrix
Quaternionic matrix
A quaternionic matrix is a matrix whose elements are quaternions.-Matrix operations:The quaternions form a noncommutative ring, and therefore addition and multiplication can be defined for quaternionic matrices as for matrices over any ring.Addition...

- matrix using quaternions as numbers
Row echelon form
Row echelon form
In linear algebra a matrix is in row echelon form if* All nonzero rows are above any rows of all zeroes, and...

— a matrix in this form is the result of applying the forward elimination procedure to a matrix (as used in Gaussian elimination
Gaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...

).
Wronskian
Wronskian
In mathematics, the Wronskian is a determinant introduced by and named by . It is used in the study of differential equations, where it can sometimes be used to show that a set of solutions is linearly independent.-Definition:...

— the determinant of a matrix of functions and their derivatives such that row n is the (n-1)^th derivative of row one.

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.