
Band matrix
Encyclopedia
In mathematics
, particularly matrix theory, a band matrix is a sparse matrix
whose non-zero entries are confined to a diagonal band, comprising the main diagonal and zero or more diagonals on either side.
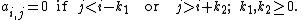
then the quantities k1 and k2 are called the left and right half-bandwidth, respectively . The bandwidth of the matrix is k1 + k2 + 1 (in other words, it is the smallest number of adjacent diagonals to which the non-zero elements are confined).
A matrix is called a band matrix or banded matrix if its bandwidth is reasonably small.
A band matrix with k1 = k2 = 0 is a diagonal matrix
; a band matrix with k1 = k2 = 1 is a tridiagonal matrix; when k1 = k2 = 2 one has a pentadiagonal matrix
and so on. If one puts k1 = 0, k2 = n−1, one obtains the definition of an upper triangular matrix
; similarly, for k1 = n−1, k2 = 0 one obtains a lower triangular matrix.
, matrices from finite element or finite difference
problems are often banded. Such matrices can be viewed as descriptions of the coupling between the problem variables; the bandedness corresponds to the fact that variables are not coupled over arbitrarily large distances. Such matrices can be further divided - for instance, banded matrices exist where every element in the band is nonzero. These often arise when discretising one-dimensional problems.
Problems in higher dimensions also lead to banded matrices, in which case the band itself also tends to be sparse. For instance, a partial differential equation on a square domain (using central differences) will yield a matrix with a half-bandwidth equal to the square root of the matrix dimension, but inside the band only 5 diagonals are nonzero. Unfortunately, applying Gaussian elimination
(or equivalently an LU decomposition
) to such a matrix results in the band being filled in by many non-zero elements.
For example, a tridiagonal matrix has bandwidth 3. The 6-by-6 matrix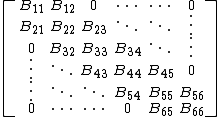
is stored as the 6-by-3 matrix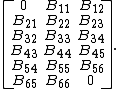
A further saving is possible when the matrix is symmetric. For example, consider a symmetric 6-by-6 matrix with a right bandwidth of 2:
This matrix is stored as the 6-by-3 matrix:
As sparse matrices lend themselves to more efficient computation than dense matrices, as well as in more efficient utilization of computer storage, there has been much research focused on finding ways to minimise the bandwidth (or directly minimise the fill in) by applying permutations to the matrix, or other such equivalence or similarity transformations.
The Cuthill–McKee algorithm can be used to reduce the bandwidth of a sparse symmetric matrix. There are, however, matrices for which the reverse Cuthill–McKee algorithm performs better. There are many other methods in use.
The problem of finding a representation of a matrix with minimal bandwidth by means of permutations of rows and columns is NP-hard
.
The inverses of Lehmer matrices are constant tridiagonal matrices, and are thus band matrices.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly matrix theory, a band matrix is a sparse matrix
Sparse matrix
In the subfield of numerical analysis, a sparse matrix is a matrix populated primarily with zeros . The term itself was coined by Harry M. Markowitz....
whose non-zero entries are confined to a diagonal band, comprising the main diagonal and zero or more diagonals on either side.
Matrix bandwidth
Formally, consider an n×n matrix A=(ai,j ). If all matrix elements are zero outside a diagonally bordered band whose range is determined by constants k1 and k2: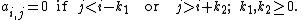
then the quantities k1 and k2 are called the left and right half-bandwidth, respectively . The bandwidth of the matrix is k1 + k2 + 1 (in other words, it is the smallest number of adjacent diagonals to which the non-zero elements are confined).
A matrix is called a band matrix or banded matrix if its bandwidth is reasonably small.
A band matrix with k1 = k2 = 0 is a diagonal matrix
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
; a band matrix with k1 = k2 = 1 is a tridiagonal matrix; when k1 = k2 = 2 one has a pentadiagonal matrix
Pentadiagonal matrix
In linear algebra, a pentadiagonal matrix is a matrix that is nearly diagonal; to be exact, it is a matrix in which the only nonzero entries are on the main diagonal, and the first two diagonals above and below it...
and so on. If one puts k1 = 0, k2 = n−1, one obtains the definition of an upper triangular matrix
Triangular matrix
In the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
; similarly, for k1 = n−1, k2 = 0 one obtains a lower triangular matrix.
Applications
In numerical analysisNumerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, matrices from finite element or finite difference
Finite difference
A finite difference is a mathematical expression of the form f − f. If a finite difference is divided by b − a, one gets a difference quotient...
problems are often banded. Such matrices can be viewed as descriptions of the coupling between the problem variables; the bandedness corresponds to the fact that variables are not coupled over arbitrarily large distances. Such matrices can be further divided - for instance, banded matrices exist where every element in the band is nonzero. These often arise when discretising one-dimensional problems.
Problems in higher dimensions also lead to banded matrices, in which case the band itself also tends to be sparse. For instance, a partial differential equation on a square domain (using central differences) will yield a matrix with a half-bandwidth equal to the square root of the matrix dimension, but inside the band only 5 diagonals are nonzero. Unfortunately, applying Gaussian elimination
Gaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
(or equivalently an LU decomposition
LU decomposition
In linear algebra, LU decomposition is a matrix decomposition which writes a matrix as the product of a lower triangular matrix and an upper triangular matrix. The product sometimes includes a permutation matrix as well. This decomposition is used in numerical analysis to solve systems of linear...
) to such a matrix results in the band being filled in by many non-zero elements.
Band storage
Band matrices are usually stored by storing the diagonals in the band; the rest is implicitly zero.For example, a tridiagonal matrix has bandwidth 3. The 6-by-6 matrix
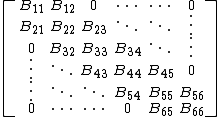
is stored as the 6-by-3 matrix
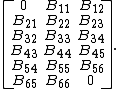
A further saving is possible when the matrix is symmetric. For example, consider a symmetric 6-by-6 matrix with a right bandwidth of 2:

This matrix is stored as the 6-by-3 matrix:

Band form of sparse matrices
From a computational point of view, working with band matrices is always preferential to working with similarly dimensioned square matrices. A band matrix can be likened in complexity to a rectangular matrix whose row dimension is equal to the bandwidth of the band matrix. Thus the work involved in performing operations such as multiplication falls significantly, often leading to huge savings in terms of calculation time and complexity.As sparse matrices lend themselves to more efficient computation than dense matrices, as well as in more efficient utilization of computer storage, there has been much research focused on finding ways to minimise the bandwidth (or directly minimise the fill in) by applying permutations to the matrix, or other such equivalence or similarity transformations.
The Cuthill–McKee algorithm can be used to reduce the bandwidth of a sparse symmetric matrix. There are, however, matrices for which the reverse Cuthill–McKee algorithm performs better. There are many other methods in use.
The problem of finding a representation of a matrix with minimal bandwidth by means of permutations of rows and columns is NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
.
Examples and special cases
The following are special cases of band matrices:- Diagonal matricesDiagonal matrixIn linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
. - Tridiagonal matrices.
- Pentadiagonal matricesPentadiagonal matrixIn linear algebra, a pentadiagonal matrix is a matrix that is nearly diagonal; to be exact, it is a matrix in which the only nonzero entries are on the main diagonal, and the first two diagonals above and below it...
. - Upper and lower triangular matricesTriangular matrixIn the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
. - Upper and lower Hessenberg matricesHessenberg matrixIn linear algebra, a Hessenberg matrix is a special kind of square matrix, one that is "almost" triangular. To be exact, an upper Hessenberg matrix has zero entries below the first subdiagonal, and a lower Hessenberg matrix has zero entries above the first superdiagonal...
. - Block-diagonal matrices.
- Shift matricesShift matrixIn mathematics, a shift matrix is a binary matrix with ones only on the superdiagonal or subdiagonal, and zeroes elsewhere. A shift matrix U with ones on the superdiagonal is an upper shift matrix....
and shear matricesShear matrixIn mathematics, a shear matrix or transvection is an elementary matrix that represents the addition of a multiple of one row or column to another...
. - Matrices in Jordan normal formJordan normal formIn linear algebra, a Jordan normal form of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called Jordan matrix, representing the operator on some basis...
. - A skyline matrixSkyline matrixA skyline matrix, or a variable band matrix, or envelope storage scheme is a form of a sparse matrix storage format matrix that reduces the storage requirement of a matrix more than banded storage. In banded storage, all entries within a fixed distance from the diagonal are stored...
, also called "variable band matrix" is a generalization of band matrix
The inverses of Lehmer matrices are constant tridiagonal matrices, and are thus band matrices.

