
Pascal matrix
Encyclopedia
In mathematics
, particularly matrix theory and combinatorics
, the Pascal matrix is an infinite matrix containing the binomial coefficients as its elements. There are three ways to achieve this: as either an upper-triangular matrix
, a lower-triangular matrix, or a symmetric matrix. The 5×5 truncations of these are shown below.
Upper triangular: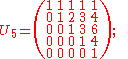
lower triangular:
symmetric: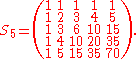
These matrices have the pleasing relationship Sn = LnUn. From this it is easily seen that all three matrices have determinant 1, as the determinant of a triangular matrix is simply the product of its diagonal elements, which are all 1 for both Ln and Un. In other words, matrices Sn, Ln, and Un are unimodular
, with Ln and Un having trace n.
The elements of the symmetric Pascal matrix are the binomial coefficients, i.e.

In other words,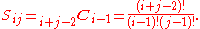
Thus the trace of Sn is given by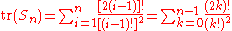
with the first few terms given by the sequence 1, 3, 9, 29, 99, 351, 1275, … .
of a special subdiagonal or superdiagonal matrix. The example below constructs a 7-by-7 Pascal matrix, but the method works for any desired n×n Pascal matrices. (Note that dots in the following matrices represent zero elements.)

It is important to note that one cannot simply assume exp(A)exp(B) = exp(A + B), for A and B n×n matrices. Such an identity only holds when AB = BA (i.e. the matrices A and B commute). In the construction of symmetric Pascal matrices like that above, the sub- and superdiagonal matrices do not commute, so the (perhaps) tempting simplification involving the addition of the matrices cannot be made.
A useful property of the sub- and superdiagonal matrices used in the construction is that both are nilpotent
; that is, when raised to a sufficiently high integer power, they degenerate into the zero matrix. (See shift matrix
for further details.) As the n×n generalised shift matrices we are using become zero when raised to power n, when calculating the matrix exponential we need only consider the first n + 1 terms of the infinite series to obtain an exact result.
The first example below uses the squares of the values of the log-matrix and constructs a 7-by-7 "Laguerre"- matrix (or matrix of coefficients of Laguerre-polynomials)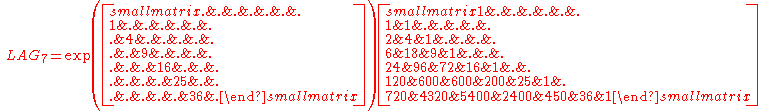
The Laguerre-matrix is actually used with some other scaling and/or the scheme of alternating signs.
(Literature about generalizations to higher powers is not found yet)
The second example below uses the products v(v + 1) of the values of the log-matrix and constructs a 7-by-7 "Lah"- matrix (or matrix of coefficients of Lah numbers)

Using v(v − 1) instead provides a diagonal shifting to bottom-right.
The third example below uses the square of the original PL7-matrix, divided by 2, in other words: the first-order binomials (binomial(k, 2) ) in the second subdiagonal and constructs a matrix, which occurs in context of the derivatives and integrals of the Gaussian error function
:
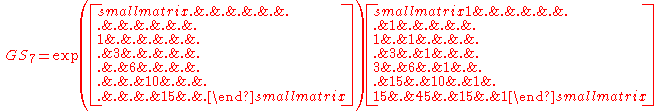
If this matrix is inverted (using, for instance, the negative matrix-logarithm), then this matrix has alternating signs and gives the coefficients of the derivatives (and by extension) the integrals of the Gauss' error-function . (Literature about generalizations to higher powers is not found yet.)
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly matrix theory and combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, the Pascal matrix is an infinite matrix containing the binomial coefficients as its elements. There are three ways to achieve this: as either an upper-triangular matrix
Triangular matrix
In the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
, a lower-triangular matrix, or a symmetric matrix. The 5×5 truncations of these are shown below.
Upper triangular:
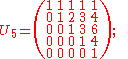
lower triangular:

symmetric:
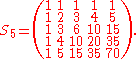
These matrices have the pleasing relationship Sn = LnUn. From this it is easily seen that all three matrices have determinant 1, as the determinant of a triangular matrix is simply the product of its diagonal elements, which are all 1 for both Ln and Un. In other words, matrices Sn, Ln, and Un are unimodular
Unimodular matrix
In mathematics, a unimodular matrix M is a square integer matrix with determinant +1 or −1. Equivalently, it is an integer matrix that is invertible over the integers: there is an integer matrix N which is its inverse...
, with Ln and Un having trace n.
The elements of the symmetric Pascal matrix are the binomial coefficients, i.e.

In other words,
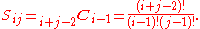
Thus the trace of Sn is given by
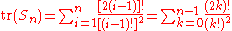
with the first few terms given by the sequence 1, 3, 9, 29, 99, 351, 1275, … .
Construction
The Pascal matrix can actually be constructed by taking the matrix exponentialMatrix exponential
In mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. Abstractly, the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group....
of a special subdiagonal or superdiagonal matrix. The example below constructs a 7-by-7 Pascal matrix, but the method works for any desired n×n Pascal matrices. (Note that dots in the following matrices represent zero elements.)

It is important to note that one cannot simply assume exp(A)exp(B) = exp(A + B), for A and B n×n matrices. Such an identity only holds when AB = BA (i.e. the matrices A and B commute). In the construction of symmetric Pascal matrices like that above, the sub- and superdiagonal matrices do not commute, so the (perhaps) tempting simplification involving the addition of the matrices cannot be made.
A useful property of the sub- and superdiagonal matrices used in the construction is that both are nilpotent
Nilpotent
In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
; that is, when raised to a sufficiently high integer power, they degenerate into the zero matrix. (See shift matrix
Shift matrix
In mathematics, a shift matrix is a binary matrix with ones only on the superdiagonal or subdiagonal, and zeroes elsewhere. A shift matrix U with ones on the superdiagonal is an upper shift matrix....
for further details.) As the n×n generalised shift matrices we are using become zero when raised to power n, when calculating the matrix exponential we need only consider the first n + 1 terms of the infinite series to obtain an exact result.
Variants
Interesting variants can be obtained by obvious modification of the matrix-logarithm PL7 and then application of the matrix exponential.The first example below uses the squares of the values of the log-matrix and constructs a 7-by-7 "Laguerre"- matrix (or matrix of coefficients of Laguerre-polynomials)
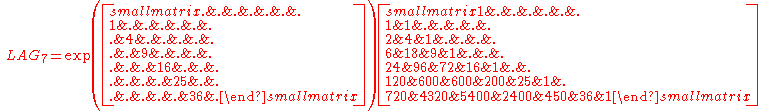
The Laguerre-matrix is actually used with some other scaling and/or the scheme of alternating signs.
(Literature about generalizations to higher powers is not found yet)
The second example below uses the products v(v + 1) of the values of the log-matrix and constructs a 7-by-7 "Lah"- matrix (or matrix of coefficients of Lah numbers)

Using v(v − 1) instead provides a diagonal shifting to bottom-right.
The third example below uses the square of the original PL7-matrix, divided by 2, in other words: the first-order binomials (binomial(k, 2) ) in the second subdiagonal and constructs a matrix, which occurs in context of the derivatives and integrals of the Gaussian error function
Error function
In mathematics, the error function is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations...
:
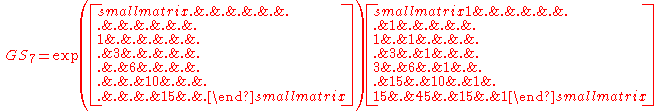
If this matrix is inverted (using, for instance, the negative matrix-logarithm), then this matrix has alternating signs and gives the coefficients of the derivatives (and by extension) the integrals of the Gauss' error-function . (Literature about generalizations to higher powers is not found yet.)
External links
- G. Helms Pascalmatrix in a project of compilation of facts about binomial&related matrices
- G. Helms Gauss-matrix
- Weisstein, Eric W. Gaussian-function
- Weisstein, Eric W. Erf-function
- Weisstein, Eric W. "Hermite Polynomial." Hermite-polynomials
- Endl, Kurt "Über eine ausgezeichnete Eigenschaft der Koeffizientenmatrizen des Laguerreschen und des Hermiteschen Polynomsystems". In: PERIODICAL VOLUME 65 Mathematische Zeitschrift Kurt Endl
- "Coefficients of unitary Hermite polynomials Hen(x)" in the "Online Encyclopedia of Integer Sequences" (OEIS) A066325 (Related to Gauss-matrix).

