
Stochastic matrix
Encyclopedia
In mathematics
, a stochastic matrix (also termed probability matrix, transition matrix, substitution matrix, or Markov matrix) is a matrix
used to describe the transitions of a Markov chain
. It has found use in probability theory
, statistics
and linear algebra
, as well as computer science
. There are several different definitions and types of stochastic matrices;
In the same vein, one may define a stochastic vector as a vector whose elements consist of nonnegative real numbers which sum to 1. Thus, each row (or column) of a stochastic matrix is a probability vector
, which are sometimes called stochastic vectors.
A common convention in English language mathematics literature is to use the right stochastic matrix; this article follows that convention.
 over a finite state space
over a finite state space
S.
If the probability
of moving from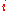 to
to 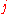 in one time step is
in one time step is 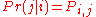 , the stochastic matrix P is given by using
, the stochastic matrix P is given by using 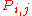 as the
as the  row and
row and 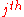 column element, e.g.,
column element, e.g.,
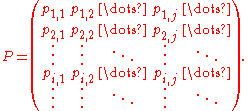
Since the probability of transitioning from state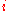 to some state must be 1, we have that this matrix is a right stochastic matrix, so that
to some state must be 1, we have that this matrix is a right stochastic matrix, so that
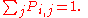
The probability of transitioning from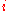 to
to 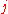 in two steps is then given by the
in two steps is then given by the 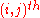 element of the square of
element of the square of 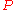 :
:
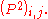
In general the probability transition of going from any state to another state in a finite Markov chain given by the matrix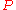 in k steps is given by
in k steps is given by 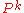 .
.
An initial distribution is given as a row vector.
A stationary probability vector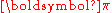 is defined as a vector that does not change under application of the transition matrix; that is, it is defined as a left eigenvector of the probability matrix, associated with eigenvalue 1:
is defined as a vector that does not change under application of the transition matrix; that is, it is defined as a left eigenvector of the probability matrix, associated with eigenvalue 1:

The Perron–Frobenius theorem
ensures that every stochastic matrix has such a vector, and that the largest absolute value of an eigenvalue is always 1. In general, there may be several such vectors. However, for a matrix with strictly positive entries, this vector is unique and can be computed by observing that for any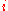 we have the following limit,
we have the following limit,

where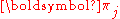 is the
is the 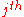 element of the row vector
element of the row vector 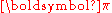 . This implies that the long-term probability of being in a state
. This implies that the long-term probability of being in a state 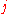 is independent of the initial state
is independent of the initial state 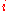 . That either of these two computations give one and the same stationary vector is a form of an ergodic theorem, which is generally true in a wide variety of dissipative dynamical systems: the system evolves, over time, to a stationary state
. That either of these two computations give one and the same stationary vector is a form of an ergodic theorem, which is generally true in a wide variety of dissipative dynamical systems: the system evolves, over time, to a stationary state
.
K gives the number of time steps the mouse stays in the game.
The Markov chain
that represents this game contains the following five states:
We use a stochastic matrix to represent the transition probabilities of this system,
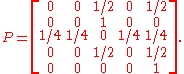
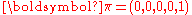 . Regardless of the initial conditions the cat will eventually catch the mouse.
. Regardless of the initial conditions the cat will eventually catch the mouse.
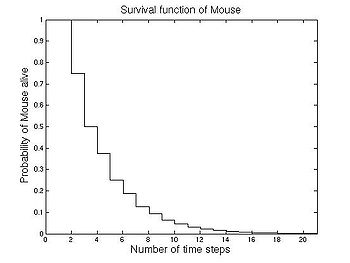 As the game has an absorbing state 5 the distribution of time to absorption is discrete phase-type distributed
As the game has an absorbing state 5 the distribution of time to absorption is discrete phase-type distributed
. Suppose the system starts in state 2, represented by the vector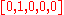 . To simplify the calculations, state five can be ignored. Let
. To simplify the calculations, state five can be ignored. Let
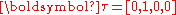
and remove state five to make a sub-stochastic matrix,
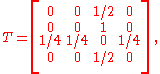 with
with 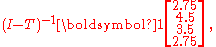
where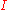 is the identity matrix
is the identity matrix
, and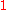 represents a column matrix of all ones.
represents a column matrix of all ones.
The expected time of the mouse's survival is given by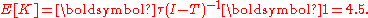
Higher order moments are given by
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a stochastic matrix (also termed probability matrix, transition matrix, substitution matrix, or Markov matrix) is a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
used to describe the transitions of a Markov chain
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
. It has found use in probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
and linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, as well as computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
. There are several different definitions and types of stochastic matrices;
- A right stochastic matrix is a square matrix each of whose rows consists of nonnegative real numbers, with each row summing to 1.
- A left stochastic matrix is a square matrix each of whose columns consist of nonnegative real numbers, with each column summing to 1.
- A doubly stochastic matrixDoubly stochastic matrixIn mathematics, especially in probability and combinatorics, a doubly stochastic matrix,is a square matrix of nonnegative real numbers, each of whose rows and columns sums to 1...
is a square matrix where all entries are nonnegative and all rows and all columns sum to 1.
In the same vein, one may define a stochastic vector as a vector whose elements consist of nonnegative real numbers which sum to 1. Thus, each row (or column) of a stochastic matrix is a probability vector
Probability vector
Stochastic vector redirects here. For the concept of a random vector, see Multivariate random variable.In mathematics and statistics, a probability vector or stochastic vector is a vector with non-negative entries that add up to one....
, which are sometimes called stochastic vectors.
A common convention in English language mathematics literature is to use the right stochastic matrix; this article follows that convention.
Definition and properties
A stochastic matrix describes a Markov chain over a finite state space
over a finite state spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
S.
If the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
of moving from
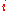 to
to 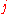 in one time step is
in one time step is 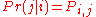 , the stochastic matrix P is given by using
, the stochastic matrix P is given by using 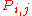 as the
as the  row and
row and 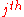 column element, e.g.,
column element, e.g.,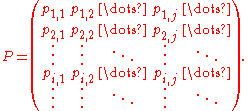
Since the probability of transitioning from state
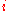 to some state must be 1, we have that this matrix is a right stochastic matrix, so that
to some state must be 1, we have that this matrix is a right stochastic matrix, so that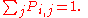
The probability of transitioning from
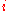 to
to 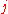 in two steps is then given by the
in two steps is then given by the 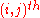 element of the square of
element of the square of 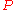 :
: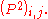
In general the probability transition of going from any state to another state in a finite Markov chain given by the matrix
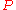 in k steps is given by
in k steps is given by 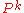 .
.An initial distribution is given as a row vector.
A stationary probability vector
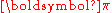 is defined as a vector that does not change under application of the transition matrix; that is, it is defined as a left eigenvector of the probability matrix, associated with eigenvalue 1:
is defined as a vector that does not change under application of the transition matrix; that is, it is defined as a left eigenvector of the probability matrix, associated with eigenvalue 1:
The Perron–Frobenius theorem
Perron–Frobenius theorem
In linear algebra, the Perron–Frobenius theorem, proved by and , asserts that a real square matrix with positive entries has a unique largest real eigenvalue and that the corresponding eigenvector has strictly positive components, and also asserts a similar statement for certain classes of...
ensures that every stochastic matrix has such a vector, and that the largest absolute value of an eigenvalue is always 1. In general, there may be several such vectors. However, for a matrix with strictly positive entries, this vector is unique and can be computed by observing that for any
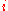 we have the following limit,
we have the following limit,
where
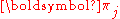 is the
is the 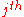 element of the row vector
element of the row vector 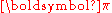 . This implies that the long-term probability of being in a state
. This implies that the long-term probability of being in a state 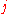 is independent of the initial state
is independent of the initial state 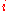 . That either of these two computations give one and the same stationary vector is a form of an ergodic theorem, which is generally true in a wide variety of dissipative dynamical systems: the system evolves, over time, to a stationary state
. That either of these two computations give one and the same stationary vector is a form of an ergodic theorem, which is generally true in a wide variety of dissipative dynamical systems: the system evolves, over time, to a stationary stateStationary state
In quantum mechanics, a stationary state is an eigenvector of the Hamiltonian, implying the probability density associated with the wavefunction is independent of time . This corresponds to a quantum state with a single definite energy...
.
Example: the cat and mouse
Suppose you have a timer and a row of five adjacent boxes, with a cat in the first box and a mouse in the fifth box at time zero. The cat and the mouse both jump to a random adjacent box when the timer advances. E.g. if the cat is in the second box and the mouse in the fourth one, the probability is one fourth that the cat will be in the first box and the mouse in the fifth after the timer advances. If the cat is in the first box and the mouse in the fifth one, the probability is one that the cat will be in box two and the mouse will be in box four after the timer advances. The cat eats the mouse if both end up in the same box, at which time the game ends. The random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
K gives the number of time steps the mouse stays in the game.
The Markov chain
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
that represents this game contains the following five states:
- State 1: cat in the first box, mouse in the third box: (1, 3)
- State 2: cat in the first box, mouse in the fifth box: (1, 5)
- State 3: cat in the second box, mouse in the fourth box: (2, 4)
- State 4: cat in the third box, mouse in the fifth box: (3, 5)
- State 5: the cat ate the mouse and the game ended: F.
We use a stochastic matrix to represent the transition probabilities of this system,
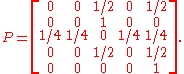
Long-term averages
As state 5 is an absorbing state the long-term average vector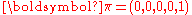 . Regardless of the initial conditions the cat will eventually catch the mouse.
. Regardless of the initial conditions the cat will eventually catch the mouse.Phase-type representation

Discrete phase-type distribution
The discrete phase-type distribution is a probability distribution that results from a system of one or more inter-related geometric distributions occurring in sequence, or phases. The sequence in which each of the phases occur may itself be a stochastic process...
. Suppose the system starts in state 2, represented by the vector
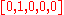 . To simplify the calculations, state five can be ignored. Let
. To simplify the calculations, state five can be ignored. Let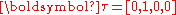
and remove state five to make a sub-stochastic matrix,
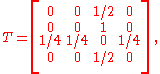 with
with 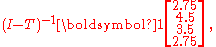
where
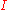 is the identity matrix
is the identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
, and
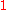 represents a column matrix of all ones.
represents a column matrix of all ones.The expected time of the mouse's survival is given by
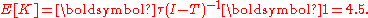
Higher order moments are given by
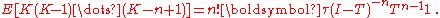
See also
- Muirhead's inequalityMuirhead's inequalityIn mathematics, Muirhead's inequality, named after Robert Franklin Muirhead, also known as the "bunching" method, generalizes the inequality of arithmetic and geometric means.-The "a-mean":For any real vectora=...
- Perron–Frobenius theoremPerron–Frobenius theoremIn linear algebra, the Perron–Frobenius theorem, proved by and , asserts that a real square matrix with positive entries has a unique largest real eigenvalue and that the corresponding eigenvector has strictly positive components, and also asserts a similar statement for certain classes of...
- Doubly stochastic matrixDoubly stochastic matrixIn mathematics, especially in probability and combinatorics, a doubly stochastic matrix,is a square matrix of nonnegative real numbers, each of whose rows and columns sums to 1...
- Discrete phase-type distributionDiscrete phase-type distributionThe discrete phase-type distribution is a probability distribution that results from a system of one or more inter-related geometric distributions occurring in sequence, or phases. The sequence in which each of the phases occur may itself be a stochastic process...
- Probabilistic automatonProbabilistic automatonIn mathematics and computer science, the probabilistic automaton is a generalization of the non-deterministic finite automaton; it includes the probability of a given transition into the transition function, turning it into a transition matrix or stochastic matrix. Thus, the probabilistic...

