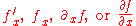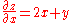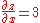Partial derivative
Encyclopedia
In mathematics
, a partial derivative of a function
of several variables is its derivative
with respect to one of those variables, with the others held constant (as opposed to the total derivative
, in which all variables are allowed to vary). Partial derivatives are used in vector calculus and differential geometry.
The partial derivative of a function f with respect to the variable x is variously denoted by
The partial-derivative symbol is ∂. The notation was introduced by Adrien-Marie Legendre
and gained general acceptance after its reintroduction by Carl Gustav Jacob Jacobi.
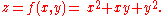
The graph
of this function defines a surface
in Euclidean space
. To every point on this surface, there are an infinite number of tangent lines. Partial differentiation is the act of choosing one of these lines and finding its slope
. Usually, the lines of most interest are those that are parallel to the xz-plane, and those that are parallel to the yz-plane.
To find the slope of the line tangent to the function at that is parallel to the xz-plane, the y variable is treated as constant. The graph and this plane are shown on the right. On the graph below it, we see the way the function looks on the plane . By finding the derivative
of the equation while assuming that y is a constant, the slope of ƒ at the point is found to be:
So at , by substitution, the slope is 3. Therefore
at the point. . That is, the partial derivative of z with respect to x at is 3.
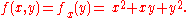
In other words, every value of x defines a function, denoted fx, which is a function of one variable. That is,
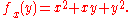
Once a value of x is chosen, say a, then f(x,y) determines a function fa which sends y to a2 + ay + y2:

In this expression, a is a constant, not a variable, so fa is a function of only one real variable, that being y. Consequently, the definition of the derivative for a function of one variable applies:

The above procedure can be performed for any choice of a. Assembling the derivatives together into a function gives a function which describes the variation of f in the y direction:

This is the partial derivative of f with respect to y. Here ∂ is a rounded d called the partial derivative symbol. To distinguish it from the letter d, ∂ is sometimes pronounced "del" or "partial" instead of "dee".
In general, the partial derivative of a function f(x1,...,xn) in the direction xi at the point (a1,...,an) is defined to be:
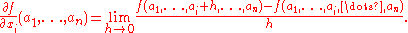
In the above difference quotient, all the variables except xi are held fixed. That choice of fixed values determines a function of one variable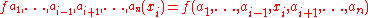 , and by definition,
, and by definition,
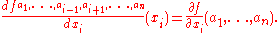
In other words, the different choices of a index a family of one-variable functions just as in the example above. This expression also shows that the computation of partial derivatives reduces to the computation of one-variable derivatives.
An important example of a function of several variables is the case of a scalar-valued function f(x1,...xn) on a domain in Euclidean space Rn (e.g., on R2 or R3). In this case f has a partial derivative ∂f/∂xj with respect to each variable xj. At the point a, these partial derivatives define the vector
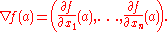
This vector is called the gradient
of f at a. If f is differentiable at every point in some domain, then the gradient is a vector-valued function ∇f which takes the point a to the vector ∇f(a). Consequently, the gradient produces a vector field
.
A common abuse of notation
is to define the del operator (∇) as follows in three-dimensional Euclidean space
R3 with unit vectors :
: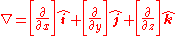
Or, more generally, for n-dimensional Euclidean space Rn with coordinates (x1, x2, x3,...,xn) and unit vectors (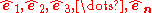 ):
):
. Let U be an open subset
of Rn and f : U → R a function. The partial derivative of f at the point a = (a1, ..., an) ∈ U with respect to the i-th variable ai is defined as

Even if all partial derivatives ∂f/∂ai(a) exist at a given point a, the function need not be continuous
there. However, if all partial derivatives exist in a neighborhood of a and are continuous there, then f is totally differentiable
in that neighborhood and the total derivative is continuous. In this case, it is said that f is a C1 function. This can be used to generalize for vector valued functions (f : U → Rm) by carefully using a componentwise argument.
The partial derivative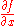 can be seen as another function defined on U and can again be partially differentiated. If all mixed second order partial derivatives are continuous at a point (or on a set), f is termed a C2 function at that point (or on that set); in this case, the partial derivatives can be exchanged by Clairaut's theorem:
can be seen as another function defined on U and can again be partially differentiated. If all mixed second order partial derivatives are continuous at a point (or on a set), f is termed a C2 function at that point (or on that set); in this case, the partial derivatives can be exchanged by Clairaut's theorem:
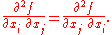
 The volume
The volume
V of a cone
depends on the cone's height
h and its radius
r according to the formula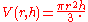
The partial derivative of V with respect to r is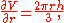
which represents the rate with which a cone's volume changes if its radius is varied and its height is kept constant. The partial derivative with respect to h is
which represents the rate with which the volume changes if its height is varied and its radius is kept constant.
By contrast, the total derivative
of V with respect to r and h are respectively
and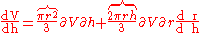
The difference between the total and partial derivative is the elimination of indirect dependencies between variables in partial derivatives.
If (for some arbitrary reason) the cone's proportions have to stay the same, and the height and radius are in a fixed ratio k,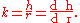
This gives the total derivative with respect to r: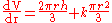
Equations involving an unknown function's partial derivatives are called partial differential equation
s and are common in physics
, engineering
, and other science
s and applied disciplines.
First-order partial derivatives:
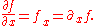
Second-order partial derivatives:
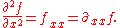
Second-order mixed derivatives:
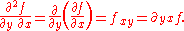
Higher-order partial and mixed derivatives:
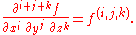
When dealing with functions of multiple variables, some of these variables may be related to each other, and it may be necessary to specify explicitly which variables are being held constant. In fields such as statistical mechanics
, the partial derivative of f with respect to x, holding y and z constant, is often expressed as
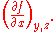
s for regular derivatives. Given a partial derivative, it allows for the partial recovery of the original function.
Consider the example of . The "partial" integral can be taken with respect to x (treating y as constant, in a similar manner to partial derivation):
. The "partial" integral can be taken with respect to x (treating y as constant, in a similar manner to partial derivation):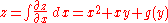
Here, the "constant" of integration is no longer a constant, but instead a function of all the variables of the original function except x. The reason for this is that all the other variables are treated as constant when taking the partial derivative, so any function which does not involve will disappear when taking the partial derivative, and we have to account for this when we take the antiderivative. The most general way to represent this is to have the "constant" represent an unknown function of all the other variables.
will disappear when taking the partial derivative, and we have to account for this when we take the antiderivative. The most general way to represent this is to have the "constant" represent an unknown function of all the other variables.
Thus the set of functions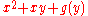 , where g is any one-argument function, represents the entire set of functions in variables x,y that could have produced the x-partial derivative 2x+y.
, where g is any one-argument function, represents the entire set of functions in variables x,y that could have produced the x-partial derivative 2x+y.
If all the partial derivatives of a function are known (for example, with the gradient
), then the antiderivatives can be matched via the above process to reconstruct the original function up to a constant.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a partial derivative of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of several variables is its derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
with respect to one of those variables, with the others held constant (as opposed to the total derivative
Total derivative
In the mathematical field of differential calculus, the term total derivative has a number of closely related meanings.The total derivative of a function f, of several variables, e.g., t, x, y, etc., with respect to one of its input variables, e.g., t, is different from the partial derivative...
, in which all variables are allowed to vary). Partial derivatives are used in vector calculus and differential geometry.
The partial derivative of a function f with respect to the variable x is variously denoted by
The partial-derivative symbol is ∂. The notation was introduced by Adrien-Marie Legendre
Adrien-Marie Legendre
Adrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...
and gained general acceptance after its reintroduction by Carl Gustav Jacob Jacobi.
Introduction
Suppose that ƒ is a function of more than one variable. For instance,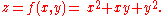
The graph
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
of this function defines a surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. To every point on this surface, there are an infinite number of tangent lines. Partial differentiation is the act of choosing one of these lines and finding its slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
. Usually, the lines of most interest are those that are parallel to the xz-plane, and those that are parallel to the yz-plane.
To find the slope of the line tangent to the function at that is parallel to the xz-plane, the y variable is treated as constant. The graph and this plane are shown on the right. On the graph below it, we see the way the function looks on the plane . By finding the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the equation while assuming that y is a constant, the slope of ƒ at the point is found to be:
So at , by substitution, the slope is 3. Therefore
at the point. . That is, the partial derivative of z with respect to x at is 3.
Basic definition
The function f can be reinterpreted as a family of functions of one variable indexed by the other variables: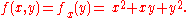
In other words, every value of x defines a function, denoted fx, which is a function of one variable. That is,
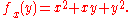
Once a value of x is chosen, say a, then f(x,y) determines a function fa which sends y to a2 + ay + y2:

In this expression, a is a constant, not a variable, so fa is a function of only one real variable, that being y. Consequently, the definition of the derivative for a function of one variable applies:

The above procedure can be performed for any choice of a. Assembling the derivatives together into a function gives a function which describes the variation of f in the y direction:

This is the partial derivative of f with respect to y. Here ∂ is a rounded d called the partial derivative symbol. To distinguish it from the letter d, ∂ is sometimes pronounced "del" or "partial" instead of "dee".
In general, the partial derivative of a function f(x1,...,xn) in the direction xi at the point (a1,...,an) is defined to be:
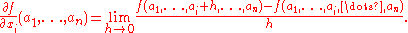
In the above difference quotient, all the variables except xi are held fixed. That choice of fixed values determines a function of one variable
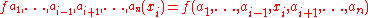 , and by definition,
, and by definition,
In other words, the different choices of a index a family of one-variable functions just as in the example above. This expression also shows that the computation of partial derivatives reduces to the computation of one-variable derivatives.
An important example of a function of several variables is the case of a scalar-valued function f(x1,...xn) on a domain in Euclidean space Rn (e.g., on R2 or R3). In this case f has a partial derivative ∂f/∂xj with respect to each variable xj. At the point a, these partial derivatives define the vector
This vector is called the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of f at a. If f is differentiable at every point in some domain, then the gradient is a vector-valued function ∇f which takes the point a to the vector ∇f(a). Consequently, the gradient produces a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
.
A common abuse of notation
Abuse of notation
In mathematics, abuse of notation occurs when an author uses a mathematical notation in a way that is not formally correct but that seems likely to simplify the exposition or suggest the correct intuition . Abuse of notation should be contrasted with misuse of notation, which should be avoided...
is to define the del operator (∇) as follows in three-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
R3 with unit vectors
 :
:
Or, more generally, for n-dimensional Euclidean space Rn with coordinates (x1, x2, x3,...,xn) and unit vectors (
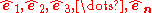 ):
):
Formal definition
Like ordinary derivatives, the partial derivative is defined as a limitLimit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
. Let U be an open subset
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
of Rn and f : U → R a function. The partial derivative of f at the point a = (a1, ..., an) ∈ U with respect to the i-th variable ai is defined as

Even if all partial derivatives ∂f/∂ai(a) exist at a given point a, the function need not be continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
there. However, if all partial derivatives exist in a neighborhood of a and are continuous there, then f is totally differentiable
Total derivative
In the mathematical field of differential calculus, the term total derivative has a number of closely related meanings.The total derivative of a function f, of several variables, e.g., t, x, y, etc., with respect to one of its input variables, e.g., t, is different from the partial derivative...
in that neighborhood and the total derivative is continuous. In this case, it is said that f is a C1 function. This can be used to generalize for vector valued functions (f : U → Rm) by carefully using a componentwise argument.
The partial derivative
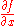 can be seen as another function defined on U and can again be partially differentiated. If all mixed second order partial derivatives are continuous at a point (or on a set), f is termed a C2 function at that point (or on that set); in this case, the partial derivatives can be exchanged by Clairaut's theorem:
can be seen as another function defined on U and can again be partially differentiated. If all mixed second order partial derivatives are continuous at a point (or on a set), f is termed a C2 function at that point (or on that set); in this case, the partial derivatives can be exchanged by Clairaut's theorem: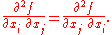
Examples

Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
V of a cone
Cone (geometry)
A cone is an n-dimensional geometric shape that tapers smoothly from a base to a point called the apex or vertex. Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base...
depends on the cone's height
Height
Height is the measurement of vertical distance, but has two meanings in common use. It can either indicate how "tall" something is, or how "high up" it is. For example "The height of the building is 50 m" or "The height of the airplane is 10,000 m"...
h and its radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
r according to the formula
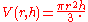
The partial derivative of V with respect to r is
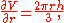
which represents the rate with which a cone's volume changes if its radius is varied and its height is kept constant. The partial derivative with respect to h is

which represents the rate with which the volume changes if its height is varied and its radius is kept constant.
By contrast, the total derivative
Total derivative
In the mathematical field of differential calculus, the term total derivative has a number of closely related meanings.The total derivative of a function f, of several variables, e.g., t, x, y, etc., with respect to one of its input variables, e.g., t, is different from the partial derivative...
of V with respect to r and h are respectively

and
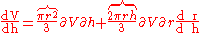
The difference between the total and partial derivative is the elimination of indirect dependencies between variables in partial derivatives.
If (for some arbitrary reason) the cone's proportions have to stay the same, and the height and radius are in a fixed ratio k,
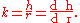
This gives the total derivative with respect to r:
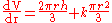
Equations involving an unknown function's partial derivatives are called partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s and are common in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
, and other science
Science
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
s and applied disciplines.
Notation
For the following examples, let f be a function in x, y and z.First-order partial derivatives:
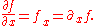
Second-order partial derivatives:
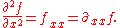
Second-order mixed derivatives:
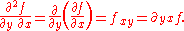
Higher-order partial and mixed derivatives:
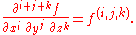
When dealing with functions of multiple variables, some of these variables may be related to each other, and it may be necessary to specify explicitly which variables are being held constant. In fields such as statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, the partial derivative of f with respect to x, holding y and z constant, is often expressed as
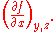
Antiderivative analogue
There is a concept for partial derivatives that is analogous to antiderivativeAntiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
s for regular derivatives. Given a partial derivative, it allows for the partial recovery of the original function.
Consider the example of
 . The "partial" integral can be taken with respect to x (treating y as constant, in a similar manner to partial derivation):
. The "partial" integral can be taken with respect to x (treating y as constant, in a similar manner to partial derivation):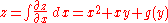
Here, the "constant" of integration is no longer a constant, but instead a function of all the variables of the original function except x. The reason for this is that all the other variables are treated as constant when taking the partial derivative, so any function which does not involve
 will disappear when taking the partial derivative, and we have to account for this when we take the antiderivative. The most general way to represent this is to have the "constant" represent an unknown function of all the other variables.
will disappear when taking the partial derivative, and we have to account for this when we take the antiderivative. The most general way to represent this is to have the "constant" represent an unknown function of all the other variables.Thus the set of functions
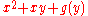 , where g is any one-argument function, represents the entire set of functions in variables x,y that could have produced the x-partial derivative 2x+y.
, where g is any one-argument function, represents the entire set of functions in variables x,y that could have produced the x-partial derivative 2x+y.If all the partial derivatives of a function are known (for example, with the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
), then the antiderivatives can be matched via the above process to reconstruct the original function up to a constant.
External links
- Partial Derivatives at MathWorld