
Euclidean distance matrix
Encyclopedia
In mathematics
, a Euclidean distance matrix is an n×n matrix
representing the spacing of a set of n points
in Euclidean space
. If A is a Euclidean distance matrix and the points are defined on m-dimensional space, then the elements of A are given by
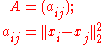
where ||.||2 denotes the 2-norm on Rm.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Euclidean distance matrix is an n×n matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
representing the spacing of a set of n points
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. If A is a Euclidean distance matrix and the points are defined on m-dimensional space, then the elements of A are given by
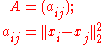
where ||.||2 denotes the 2-norm on Rm.
Properties
Simply put, the element aij describes the square of the distance between the i th and j th points in the set. By the properties of the 2-norm (or indeed, Euclidean distance in general), the matrix A has the following properties.- All elements on the diagonal of A are zero (i.e. is it a hollow matrixHollow matrixIn mathematics, a hollow matrix may refer to one of several related classes of matrix.-Diagonal entries all zero:A hollow matrix may be a square matrix whose diagonal elements are all equal to zero...
). - The trace of A is zero (by the above property).
- A is symmetric (i.e. aij = aji).
- aij1/2
 aik1/2 + akj1/2 (by the triangle inequalityTriangle inequalityIn mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
aik1/2 + akj1/2 (by the triangle inequalityTriangle inequalityIn mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
) -

- The number of unique (distinct) non-zero values within an N-by-N Euclidean distance matrix is bounded (above) by [N*(N-1)] / 2 due to the matrix being symmetric and hollow.

