
Matrix representation of conic sections
Encyclopedia
In mathematics
, the matrix representation of conic sections is one way of studying a conic section
, its axis, vertices
, foci
, tangent
s, and the relative position of a given point. We can also study conic sections whose axes aren't parallel to our coordinate system
.
Conic sections have the form of a second-degree polynomial
:

That can be written as:
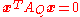
Where is the homogeneous coordinate vector
is the homogeneous coordinate vector
:

And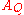 a matrix:
a matrix:

of AQ.
If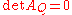 , the conic is degenerate.
, the conic is degenerate.
If Q is not degenerate, we can see what type of conic section it is by computing the minor (that is, the determinant of the submatrix resulting from removing the last row and the last column of AQ):
(that is, the determinant of the submatrix resulting from removing the last row and the last column of AQ):
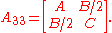
In the case of an ellipse, we can make a further distinction between an ellipse and a circle by comparing the last two diagonal elements corresponding to x2 and y2.
Moreover, in the case of a non-degenerate ellipse (with and
and 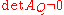 ), we have a real ellipse if
), we have a real ellipse if  but an imaginary ellipse if
but an imaginary ellipse if  . An example of the latter is
. An example of the latter is  , which has no real-valued solutions.
, which has no real-valued solutions.
If the conic section is degenerate (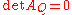 ),
),  still allows us to distinguish its form:
still allows us to distinguish its form:
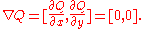
We can calculate the center by taking the first two rows of the associated
matrix , multiplying each by (x, y, 1)T, setting both inner products equal to 0, and solving the system.
, multiplying each by (x, y, 1)T, setting both inner products equal to 0, and solving the system.
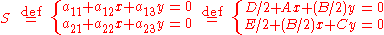
This becomes
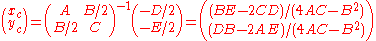
Note that in the case of a parabola, defined by (4AC-B2) = 0, there is no center since the above denominators become zero.

So we can write a canonical equation:
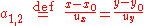
Because a 2x2 matrix has 2 eigenvectors, we obtain 2 axes.

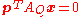
When P is on the conic, the line is the tangent there. When P is inside an ellipse, the line is the set of all points whose own associated line passes through P. This line is called the polar of the pole P with respect to the conic.
Just as P uniquely determines its polar line (with respect to a given conic), so each line determines a unique P. This is thus an expression of geometric duality
between points and lines in the plane.
As special cases, the center of a conic is the pole of the line at infinity, and each asymptote of a hyperbola is a polar (a tangent) to one of its points at infinity.
Using the theory of poles and polars, the problem of finding the four mutual tangents of two conics reduces to finding the intersection of two conics.
If and
and  are the eigenvalues
are the eigenvalues
of the matrix A33, the reduced equation can be written as
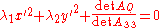
Dividing by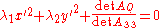 we obtain a reduced canonical equation. For example, for an ellipse:
we obtain a reduced canonical equation. For example, for an ellipse:

From here we get a and b.
The transformation
of coordinates is given by:

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the matrix representation of conic sections is one way of studying a conic section
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
, its axis, vertices
Vertex (curve)
In the geometry of curves, a vertex is a point of where the first derivative of curvature is zero. This is typically a local maximum or minimum of curvature. Other special cases may occur, for instance when the second derivative is also zero, or when the curvature is constant...
, foci
Focus (geometry)
In geometry, the foci are a pair of special points with reference to which any of a variety of curves is constructed. For example, foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola...
, tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
s, and the relative position of a given point. We can also study conic sections whose axes aren't parallel to our coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
.
Conic sections have the form of a second-degree polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
:

That can be written as:
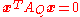
Where
 is the homogeneous coordinate vector
is the homogeneous coordinate vectorHomogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
:

And
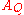 a matrix:
a matrix:
Classification
Regular and degenerated conic sections can be distinguished based on the determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of AQ.
If
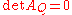 , the conic is degenerate.
, the conic is degenerate.If Q is not degenerate, we can see what type of conic section it is by computing the minor
 (that is, the determinant of the submatrix resulting from removing the last row and the last column of AQ):
(that is, the determinant of the submatrix resulting from removing the last row and the last column of AQ):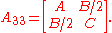
- If and only if
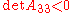 , it is a hyperbolaHyperbolaIn mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
, it is a hyperbolaHyperbolaIn mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
. - If and only if
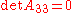 , it is a parabolaParabolaIn mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
, it is a parabolaParabolaIn mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
. - If and only if
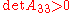 , it is an ellipseEllipseIn geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
, it is an ellipseEllipseIn geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
.
In the case of an ellipse, we can make a further distinction between an ellipse and a circle by comparing the last two diagonal elements corresponding to x2 and y2.
- If
 and
and  , it is a circle.
, it is a circle.
Moreover, in the case of a non-degenerate ellipse (with
 and
and 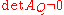 ), we have a real ellipse if
), we have a real ellipse if  but an imaginary ellipse if
but an imaginary ellipse if  . An example of the latter is
. An example of the latter is  , which has no real-valued solutions.
, which has no real-valued solutions.If the conic section is degenerate (
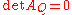 ),
),  still allows us to distinguish its form:
still allows us to distinguish its form:- If and only if
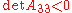 , it is two intersecting lines.
, it is two intersecting lines. - If and only if
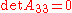 , it is two parallel straight lines. These lines are distinct and real if
, it is two parallel straight lines. These lines are distinct and real if  , coincident if
, coincident if  , and distinct and imaginary if
, and distinct and imaginary if  .
. - If and only if
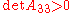 , it is a single point.
, it is a single point.
Center
In the center of the conic, the gradient of the quadratic form vanishes, so: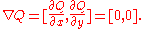
We can calculate the center by taking the first two rows of the associated
matrix
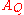 , multiplying each by (x, y, 1)T, setting both inner products equal to 0, and solving the system.
, multiplying each by (x, y, 1)T, setting both inner products equal to 0, and solving the system.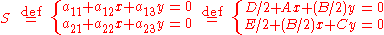
This becomes
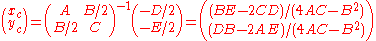
Note that in the case of a parabola, defined by (4AC-B2) = 0, there is no center since the above denominators become zero.
Axes
The major and minor axes are two lines determined by the center of the conic as a point and eigenvectors of the associated matrix as vectors of direction.
So we can write a canonical equation:
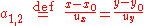
Because a 2x2 matrix has 2 eigenvectors, we obtain 2 axes.
Vertices
For a general conic we can determine its vertices by calculating the intersection of the conic and its axes — in other words, by solving the system:
Tangents
Through a given point, P, there are generally two lines tangent to a conic. Expressing P as a column vector, p, the two points of tangency are the intersections of the conic with the line whose equation is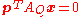
When P is on the conic, the line is the tangent there. When P is inside an ellipse, the line is the set of all points whose own associated line passes through P. This line is called the polar of the pole P with respect to the conic.
Just as P uniquely determines its polar line (with respect to a given conic), so each line determines a unique P. This is thus an expression of geometric duality
Duality (projective geometry)
A striking feature of projective planes is the "symmetry" of the roles played by points and lines in the definitions and theorems, and duality is the formalization of this metamathematical concept. There are two approaches to the subject of duality, one through language and the other a more...
between points and lines in the plane.
As special cases, the center of a conic is the pole of the line at infinity, and each asymptote of a hyperbola is a polar (a tangent) to one of its points at infinity.
Using the theory of poles and polars, the problem of finding the four mutual tangents of two conics reduces to finding the intersection of two conics.
Reduced equation
The reduced equation of a conic section is the equation of a conic section translated and rotated so that its center lies in the center of the coordinate system and its axes are parallel to the coordinate axes. This is equivalent to saying that the coordinates are moved to satisfy these properties. See the figure.If
 and
and  are the eigenvalues
are the eigenvaluesof the matrix A33, the reduced equation can be written as
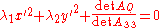
Dividing by
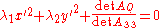 we obtain a reduced canonical equation. For example, for an ellipse:
we obtain a reduced canonical equation. For example, for an ellipse:
From here we get a and b.
The transformation
Transformation (mathematics)
In mathematics, a transformation could be any function mapping a set X on to another set or on to itself. However, often the set X has some additional algebraic or geometric structure and the term "transformation" refers to a function from X to itself that preserves this structure.Examples include...
of coordinates is given by:


