
Similar matrix
Encyclopedia
In linear algebra
, two n-by-n matrices
A and B are called similar if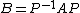
for some invertible n-by-n matrix P. Similar matrices represent the same linear transformation under two different bases
, with P being the change of basis
matrix.
The matrix P is sometimes called a similarity transformation. In the context of matrix group
s, similarity is sometimes referred to as conjugacy
, with similar matrices being conjugate.
on the space of square matrices.
Similar matrices share many properties:
There are two reasons for these facts:
Because of this, for a given matrix A, one is interested in finding a simple "normal form" B which is similar to A—the study of A then reduces to the study of the simpler matrix B. For example, A is called diagonalizable
if it is similar to a diagonal matrix
. Not all matrices are diagonalizable, but at least over the complex number
s (or any algebraically closed field
), every matrix is similar to a matrix in Jordan form. Another normal form, the rational canonical form, works over any field. By looking at the Jordan forms or rational canonical forms of A and B, one can immediately decide whether A and B are similar. The Smith normal form
can be used to determine whether matrices are similar, though unlike the Jordan and rational canonical forms, a matrix is not necessarily similar to its Smith normal form.
, given any family Pn of invertible n-by-n matrices defining a similarity transformation for all rectangular matrices sending the m-by-n matrix A into Pm−1APn, the family defines a functor
that is an automorphism of the category of all matrices, having as objects the natural numbers and morphisms from n to m the m-by-n matrices composed via matrix multiplication.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, two n-by-n matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
A and B are called similar if
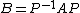
for some invertible n-by-n matrix P. Similar matrices represent the same linear transformation under two different bases
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
, with P being the change of basis
Change of basis
In linear algebra, change of basis refers to the conversion of vectors and linear transformations between matrix representations which have different bases.-Expression of a basis:...
matrix.
The matrix P is sometimes called a similarity transformation. In the context of matrix group
Matrix group
In mathematics, a matrix group is a group G consisting of invertible matrices over some field K, usually fixed in advance, with operations of matrix multiplication and inversion. More generally, one can consider n × n matrices over a commutative ring R...
s, similarity is sometimes referred to as conjugacy
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
, with similar matrices being conjugate.
Properties
Similarity is an equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on the space of square matrices.
Similar matrices share many properties:
- RankRank (linear algebra)The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
- DeterminantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
- TraceTrace (linear algebra)In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
- Eigenvalues (though the eigenvectors will in general be different)
- Characteristic polynomialCharacteristic polynomialIn linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
- Minimal polynomialMinimal polynomial (linear algebra)In linear algebra, the minimal polynomial of an n-by-n matrix A over a field F is the monic polynomial P over F of least degree such that P=0...
(among the other similarity invariants in the Smith normal formSmith normal formIn mathematics, the Smith normal form is a normal form that can be defined for any matrix with entries in a principal ideal domain . The Smith normal form of a matrix is diagonal, and can be obtained from the original matrix by multiplying on the left and right by invertible square matrices...
) - Elementary divisors
There are two reasons for these facts:
- Two similar matrices can be thought of as describing the same linear map, but with respect to different bases
- The map X P−1XP is an automorphismAutomorphismIn mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
of the associative algebraAssociative algebraIn mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
of all n-by-n matrices, as the one-object case of the above category of all matrices.
Because of this, for a given matrix A, one is interested in finding a simple "normal form" B which is similar to A—the study of A then reduces to the study of the simpler matrix B. For example, A is called diagonalizable
Diagonalizable matrix
In linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
if it is similar to a diagonal matrix
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
. Not all matrices are diagonalizable, but at least over the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s (or any algebraically closed field
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
), every matrix is similar to a matrix in Jordan form. Another normal form, the rational canonical form, works over any field. By looking at the Jordan forms or rational canonical forms of A and B, one can immediately decide whether A and B are similar. The Smith normal form
Smith normal form
In mathematics, the Smith normal form is a normal form that can be defined for any matrix with entries in a principal ideal domain . The Smith normal form of a matrix is diagonal, and can be obtained from the original matrix by multiplying on the left and right by invertible square matrices...
can be used to determine whether matrices are similar, though unlike the Jordan and rational canonical forms, a matrix is not necessarily similar to its Smith normal form.
Other areas
In group theory similarity is called conjugacy. In category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, given any family Pn of invertible n-by-n matrices defining a similarity transformation for all rectangular matrices sending the m-by-n matrix A into Pm−1APn, the family defines a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
that is an automorphism of the category of all matrices, having as objects the natural numbers and morphisms from n to m the m-by-n matrices composed via matrix multiplication.
See also
- Matrix congruenceMatrix congruenceIn mathematics, two matrices A and B over a field are called congruent if there exists an invertible matrix P over the same field such thatwhere "T" denotes the matrix transpose...
- Matrix equivalence
- Canonical forms

