.gif)
Vertex (graph theory)
Encyclopedia
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
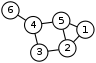
, a vertex (plural vertices) or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges (unordered pairs of vertices), while a directed graph consists of a set of vertices and a set of arcs (ordered pairs of vertices). From the point of view of graph theory, vertices are treated as featureless and indivisible objects, although they may have additional structure depending on the application from which the graph arises; for instance, a semantic network
Semantic network
A semantic network is a network which represents semantic relations among concepts. This is often used as a form of knowledge representation. It is a directed or undirected graph consisting of vertices, which represent concepts, and edges.- History :...
is a graph in which the vertices represent concepts or classes of objects.
The two vertices forming an edge are said to be the endpoints of this, and the edge is said to be incident to the vertices. A vertex w is said to be adjacent to another vertex v if the graph contains an edge (v,w). The neighborhood of a vertex v is an induced subgraph of the graph, formed by all vertices adjacent to v.
The degree
Degree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
of a vertex in a graph is the number of edges incident to it. An isolated vertex is a vertex with degree zero; that is, a vertex that is not an endpoint of any edge. A leaf vertex (also pendant vertex) is a vertex with degree one. In a directed graph, one can distinguish the outdegree (number of outgoing edges) from the indegree (number of incoming edges); a source vertex is a vertex with indegree zero, while a sink vertex is a vertex with outdegree zero.
A cut vertex is a vertex the removal of which would disconnect the remaining graph; a vertex separator
Vertex separator
In graph theory, a vertex subset S \subset V is a vertex separator for nonadjacent vertices a and b if the removal of S from the graph separates a and b into distinct connected components.-Examples:...
is a collection of vertices the removal of which would disconnect the remaining graph into small pieces. A k-vertex-connected graph
K-vertex-connected graph
In graph theory, a graph G with vertex set V is said to be k-vertex-connected if the graph remains connected when you delete fewer than k vertices from the graph...
is a graph in which removing fewer than k vertices always leaves the remaining graph connected. An independent set
Independent set (graph theory)
In graph theory, an independent set or stable set is a set of vertices in a graph, no two of which are adjacent. That is, it is a set I of vertices such that for every two vertices in I, there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in I...
is a set of vertices no two of which are adjacent, and a vertex cover
Vertex cover
In the mathematical discipline of graph theory, a vertex cover of a graph is a set of vertices such that each edge of the graph is incident to at least one vertex of the set....
is a set of vertices that includes the endpoint of each edge in the graph. The vertex space of a graph is a vector space having a set of basis vectors corresponding with the graph's vertices.
A graph is vertex-transitive
Vertex-transitive graph
In the mathematical field of graph theory, a vertex-transitive graph is a graph G such that, given any two vertices v1 and v2 of G, there is some automorphismf:V \rightarrow V\ such thatf = v_2.\...
if it has symmetries that map any vertex to any other vertex. In the context of graph enumeration
Graph enumeration
In combinatorics, an area of mathematics, graph enumeration describes a class of combinatorial enumeration problems in which one must count undirected or directed graphs of certain types, typically as a function of the number of vertices of the graph...
and graph isomorphism
Graph isomorphism
In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
it is important to distinguish between labeled vertices and unlabeled vertices. A labeled vertex is a vertex that is associated with extra information that enables it to be distinguished from other labeled vertices; two graphs can be considered isomorphic only if the correspondence between their vertices pairs up vertices with equal labels. An unlabeled vertex is one that can be substituted for any other vertex based only on its adjacencies in the graph and not based on any additional information.
Vertices in graphs are analogous to, but not the same as, vertices of polyhedra
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
: the skeleton of a polyhedron forms a graph, the vertices of which are the vertices of the polyhedron, but polyhedron vertices have additional structure (their geometric location) that is not assumed to be present in graph theory. The vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
of a vertex in a polyhedron is analogous to the neighborhood of a vertex in a graph.
In a directed graph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
, the forward star of a vertex
 is defined as its outgoing edges. In a Graph
is defined as its outgoing edges. In a Graph  with the set of vertices
with the set of vertices  and the set of edges
and the set of edges  , the forward star of
, the forward star of  can be described as
can be described as

