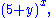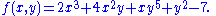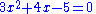Polynomial
Encyclopedia
In mathematics
, a polynomial is an expression
of finite length constructed from variables
(also known as indeterminates
) and constant
s, using only the operations of addition
, subtraction
, multiplication
, and non-negative integer
exponents
. For example, is a polynomial, but is not, because its second term
involves division by the variable x (4/x) and because its third term contains an exponent that is not an integer (3/2). The term "polynomial" can also be used as an adjective, for quantities that can be expressed as a polynomial of some parameter, as in "polynomial time" which is used in computational complexity theory
.
Polynomial comes from the Greek poly, "many" and medieval Latin binomium, "binomial
". The word was introduced in Latin by Franciscus Vieta.
Polynomials appear in a wide variety of areas of mathematics and science. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problems
to complicated problems in the sciences; they are used to define polynomial functions, which appear in settings ranging from basic chemistry
and physics
to economics
and social science; they are used in calculus
and numerical analysis
to approximate other functions. In advanced mathematics, polynomials are used to construct polynomial ring
s, a central concept in abstract algebra
and algebraic geometry
.
. The number of terms is finite. These terms consist of a constant (called the coefficient
of the term) which may be multiplied by a finite number of variables
(usually represented by letters), also called indeterminates
. Each variable may have an exponent that is a non-negative integer, i.e., a natural number
. The exponent on a variable in a term is called the degree
of that variable in that term, the degree of the term is the sum of the degrees of the variables in that term, and the degree of a polynomial is the largest degree of any one term. Since , the degree of a variable without a written exponent is one. A term with no variables is called a constant term
, or just a constant. The degree of a (nonzero) constant term is 0. The coefficient of a term may be any number from a specified set. If that set is the set of real numbers, we speak of "polynomials over the reals". Other common kinds of polynomials are polynomials with integer coefficients, polynomials with complex coefficients, and polynomials with coefficients that are integers modulo
of some prime number
p. In most of the examples in this section, the coefficients are integers.
For example:
is a term. The coefficient is –5, the variables are x and y, the degree of x is in the term two, while the degree of y is one.
The degree of the entire term is the sum of the degrees of each variable in it, so in this example the degree is 2 + 1 = 3.
Forming a sum of several terms produces a polynomial. For example, the following is a polynomial:

It consists of three terms: the first is degree two, the second is degree one, and the third is degree zero.
The commutative law of addition can be used to freely permute terms into any preferred order.
In polynomials with one variable, the terms are usually ordered according to degree, either in "descending powers of x", with the term of largest degree first, or in "ascending powers of x". The polynomial in the example above is written in descending powers of x. The first term has coefficient 3, variable x, and exponent 2. In the second term, the coefficient . The third term is a constant. Since the degree of a non-zero polynomial is the largest degree of any one term, this polynomial has degree two.
Two terms with the same variables raised to the same powers are called "like terms", and they can be combined (after having been made adjacent) using the distributive law into a single term, whose coefficient is the sum of the coefficients of the terms that were combined. It may happen that this makes the coefficient 0, in which case their combination just cancels out the terms. Polynomials can be added using the associative law of addition (which simply groups all their terms together into a single sum), possibly followed by reordering, and combining of like terms. For example, if

then
which can be simplified to
To work out the product of two polynomials into a sum of terms, the distributive law is repeatedly applied, with as result that each term of one polynomial multiplied by every term of the other. For example, if
then
which can be simplified to
The sum or product of two polynomials is always a polynomial.
, subtraction
, multiplication
, and raising expressions to constant positive whole number power
s. Such an expression can always be rewritten as a sum of terms. For example, (x + 1)3 is a polynomial; its standard form is x3 + 3x2 + 3x + 1.
Division of one polynomial by another does not, in general, produce a polynomial, but rather produces a quotient and a remainder. A formal quotient of polynomials, that is, an algebraic fraction where the numerator and denominator are polynomials, is called a "rational expression
" or "rational fraction" and is not, in general, a polynomial. Division of a polynomial by a number, however, does yield another polynomial. For example,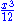
is considered a valid term in a polynomial (and a polynomial by itself) because it is equivalent to and
and  is just a constant. When this expression is used as a term, its coefficient is therefore
is just a constant. When this expression is used as a term, its coefficient is therefore  . For similar reasons, if complex coefficients are allowed, one may have a single term like
. For similar reasons, if complex coefficients are allowed, one may have a single term like  ; even though it looks like it should be expanded to two terms, the complex number 2 + 3i is one complex number, and is the coefficient of that term.
; even though it looks like it should be expanded to two terms, the complex number 2 + 3i is one complex number, and is the coefficient of that term.
is not a polynomial because it includes division by a non-constant polynomial.
is not a polynomial, because it contains a variable used as exponent.
Since subtraction can be replaced by addition of the opposite quantity, and since positive whole number exponents can be replaced by repeated multiplication, all polynomials can be constructed from constants and variables using only addition and multiplication.
a polynomial. A function ƒ of one argument
is called a polynomial function if it satisfies
for all arguments x, where n is a non-negative integer and a0, a1,a2, ..., an are constant coefficients.
For example, the function ƒ, taking real numbers to real numbers, defined by

is a polynomial function of one argument. Polynomial functions of multiple arguments can also be defined, using polynomials in multiple variables, as in
An example is also the function which, although it doesn't look like a polynomial, is a polynomial function since for every x it is true that
which, although it doesn't look like a polynomial, is a polynomial function since for every x it is true that 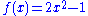 (see Chebyshev polynomials
(see Chebyshev polynomials
).
Polynomial functions are a class of functions having many important properties. They are all continuous
, smooth
, entire
, computable
, etc.
in which a polynomial is set equal to another polynomial.
is a polynomial equation. In case of a univariate polynomial equation, the variable is considered an unknown
, and one seeks to find the possible values for which both members of the equation evaluate to the same value (in general more than one solution may exist). A polynomial equation is to be contrasted with a polynomial identity like , where both members represent the same polynomial in different forms, and as a consequence any evaluation of both members will give a valid equality. This means that a polynomial identity is a polynomial equation for which all possible values of the unknowns are solutions.
Polynomials serve to approximate other functions
, such as sine
, cosine, and exponential
.
All polynomials have an expanded form, in which the distributive and associative laws have been used to remove all brackets and commutative law has been used to make the like terms adjacent and combine them. All polynomials with coefficients in a unique factorization domain
(for example, the integers or a field
also have a factored form in which the polynomial is written as a product of irreducible polynomial
s and a constant. In the case of the field of complex numbers, the irreducible polynomials are linear.
For example, the factored form of
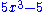
is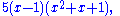
over the integers and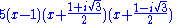
over the complex numbers.
Every polynomial in one variable is equivalent to a polynomial with the form

This form is sometimes taken as the definition of a polynomial in one variable.
Evaluation of a polynomial consists of assigning a number to each variable and carrying out the indicated multiplications and additions. Actual evaluation is usually more efficient using the Horner scheme
:
In elementary algebra
, methods are given for solving all first degree and second degree polynomial equations in one variable. In the case of polynomial equations, the variable is often called an unknown. The number of solutions may not exceed the degree, and will equal the degree when multiplicity
of solutions and complex number solutions are counted. This fact is called the fundamental theorem of algebra.
A system of polynomial equations is a set of equations in which each variable must take on the same value everywhere it appears in any of the equations. Systems of equations are usually grouped with a single open brace on the left. In elementary algebra
, in particular in linear algebra
, methods are given for solving a system of linear equations in several unknowns. If there are more unknowns than equations, the system is called underdetermined. If there are more equations than unknowns, the system is called overdetermined
. Overdetermined systems are common in practical applications. For example, one U.S. mapping survey used computers to solve 2.5 million equations in 400,000 unknowns.
Viète's formulas relate the coefficients of a polynomial to symmetric polynomial
functions of its roots.
, circa 200 BCE, begins "Three sheafs of good crop, two sheafs of mediocre crop, and one sheaf of bad crop are sold for 29 dou." We would write 3x + 2y + z = 29.
's The Whetstone of Witte, 1557. The signs + for addition, − for subtraction, and the use of a letter for an unknown appear in Michael Stifel
's Arithemetica integra, 1544. René Descartes
, in La géometrie, 1637, introduced the concept of the graph of a polynomial equation. He popularized the use of letters from the beginning of the alphabet to denote constants and letters from the end of the alphabet to denote variables, as can be seen above, in the general formula for a polynomial in one variable, where the a 's denote constants and x denotes a variable. Descartes introduced the use of superscripts to denote exponents as well.
Some polynomials, such as x2 + 1, do not have any roots among the real number
s. If, however, the set of allowed candidates is expanded to the complex number
s, every non-constant polynomial has at least one root; this is the fundamental theorem of algebra
. By successively dividing out factors x − a, one sees that any polynomial with complex coefficients can be written as a constant (its leading coefficient) times a product of such polynomial factors of degree 1; as a consequence the number of (complex) roots counted with their multiplicities is exactly equal to the degree of the polynomial.
There is a difference between approximating roots and finding exact expressions for roots. Formulas for expressing the roots of polynomials of degree 2 in terms of square roots have been known since ancient times (see quadratic equation
), and for polynomials of degree 3 or 4 similar formulas (using cube roots in addition to square roots) were found in the 16th century (see cubic function
and quartic function
for the formulas and Niccolo Fontana Tartaglia
, Lodovico Ferrari
, Gerolamo Cardano
, and Vieta for historical details). But formulas for degree 5 eluded researchers. In 1824, Niels Henrik Abel
proved the striking result that there can be no general (finite) formula, involving only arithmetic operations and radicals, that expresses the roots of a polynomial of degree 5 or greater in terms of its coefficients (see Abel-Ruffini theorem). In 1830, Évariste Galois
, studying the permutations of the roots of a polynomial, extended Abel-Ruffini theorem by showing that, given a polynomial equation, one may decide if it is solvable by radicals, and, if it is, solve it. This result marked the start of Galois theory
and Group theory
, two important branches of modern mathematics. Galois himself noted that the computations implied by his method were impracticable. Nevertheless formulas for solvable equations of degrees 5 and 6 have been published (see quintic function and sextic equation
).
Numerical approximations of roots of polynomial equations in one unknown is easily done on a computer by the Jenkins-Traub method, Laguerre's method
, Durand–Kerner method or by some other root-finding algorithm
.
For polynomials in more than one variable the notion of root does not exist, and there are usually infinitely many combinations of values for the variables for which the polynomial function takes the value zero. However for certain sets of such polynomials it may happen that for only finitely many combinations all polynomial functions take the value zero.
For a set of polynomial equations in several unknowns, there are algorithm
s to decide if they have a finite number of complex solutions. If the number of solutions is finite, there are algorithms to compute the solutions. The methods underlying these algorithms are described in the article systems of polynomial equations
.
The special case where all the polynomials are of degree one is called a system of linear equations, for which another range of different solution methods exist, including the classical Gaussian elimination
.
It has been shown by Richard Birkeland and Karl Meyr that the roots of any polynomial may be expressed in terms of multivariate hypergeometric functions. Ferdinand von Lindemann
and Hiroshi Umemura showed that the roots may also be expressed in terms of Siegel modular functions, generalizations of the theta functions that appear in the theory of elliptic function
s. These characterisations of the roots of arbitrary polynomials are generalisations of the methods previously discovered to solve the quintic equation
.
.
.
The graph of a non-constant (univariate) polynomial always tends to infinity when the variable increases indefinitely (in absolute value
).
Polynomial graphs are analyzed in calculus using intercepts, slopes, concavity, and end behavior.
The illustrations below show graphs of polynomials.
, which roughly states that every differentiable function locally looks like a polynomial function, and the Stone-Weierstrass theorem
, which states that every continuous function
defined on a compact
interval
of the real axis can be approximated on the whole interval as closely as desired by a polynomial function. Polynomial functions are also frequently used to interpolate
functions.
Calculating derivatives and integrals of polynomial functions is particularly simple. For the polynomial function
the derivative with respect to x is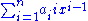
and the indefinite integral is
, one distinguishes between polynomials and polynomial functions. A polynomial f in one variable X over a ring
R is defined to be a formal expression of the form
where n is a natural number, the coefficients are elements of R, and X is a formal symbol, whose powers Xi are just placeholders for the corresponding coefficients ai, so that the given formal expression is just a way to encode the sequence
are elements of R, and X is a formal symbol, whose powers Xi are just placeholders for the corresponding coefficients ai, so that the given formal expression is just a way to encode the sequence 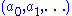 , where there is an n such that ai = 0 for all i > n. Two polynomials sharing the same value of n are considered to be equal if and only if the sequences of their coefficients are equal; furthermore any polynomial is equal to any polynomial with greater value of n obtained from it by adding terms in front whose coefficient is zero. These polynomials can be added by simply adding corresponding coefficients (the rule for extending by terms with zero coefficients can be used to make sure such coefficients exist). Thus each polynomial is actually equal to the sum of the terms used in its formal expression, if such a term aiXi is interpreted as a polynomial that has zero coefficients at all powers of X other than Xi. Then to define multiplication, it suffices by the distributive law to describe the product of any two such terms, which is given by the rule
, where there is an n such that ai = 0 for all i > n. Two polynomials sharing the same value of n are considered to be equal if and only if the sequences of their coefficients are equal; furthermore any polynomial is equal to any polynomial with greater value of n obtained from it by adding terms in front whose coefficient is zero. These polynomials can be added by simply adding corresponding coefficients (the rule for extending by terms with zero coefficients can be used to make sure such coefficients exist). Thus each polynomial is actually equal to the sum of the terms used in its formal expression, if such a term aiXi is interpreted as a polynomial that has zero coefficients at all powers of X other than Xi. Then to define multiplication, it suffices by the distributive law to describe the product of any two such terms, which is given by the rule
Thus the set of all polynomials with coefficients in the ring R forms itself a ring, the ring of polynomials over R, which is denoted by R[X]. The map from R to R[X] sending r to rX0 is an injective homomorphism of rings, by which R is viewed as a subring of R[X]. If R is commutative
, then R[X] is an algebra
over R.
One can think of the ring R[X] as arising from R by adding one new element X to R, and extending in a minimal way to a ring in which X satisfies no other relations than the obligatory ones, plus commutation with all elements of R (that is ). To do this, one must add all powers of X and their linear combinations as well.
Formation of the polynomial ring, together with forming factor rings by factoring out ideals
, are important tools for constructing new rings out of known ones. For instance, the ring (in fact field) of complex numbers, which can be constructed from the polynomial ring R[X] over the real numbers by factoring out the ideal of multiples of the polynomial . Another example is the construction of finite field
s, which proceeds similarly, starting out with the field of integers modulo some prime number
as the coefficient ring R (see modular arithmetic
).
If R is commutative, then one can associate to every polynomial P in R[X], a polynomial function f with domain and range equal to R (more generally one can take domain and range to be the same unital associative algebra
over R). One obtains the value f(r) by substitution
of the value r for the symbol X in P. One reason to distinguish between polynomials and polynomial functions is that over some rings different polynomials may give rise to the same polynomial function (see Fermat's little theorem
for an example where R is the integers modulo p). This is not the case when R is the real or complex numbers, whence the two concepts are not always distinguished in analysis. An even more important reason to distinguish between polynomials and polynomial functions is that many operations on polynomials (like Euclidean division) require looking at what a polynomial is composed of as an expression rather than evaluating it at some constant value for X. And it should be noted that if R is not commutative, there is no (well behaved) notion of polynomial function at all.
, one major focus of study is divisibility among polynomials. If R is an integral domain and f and g are polynomials in R[X], it is said that f divides g or f is a divisor of g if there exists a polynomial q in R[X] such that f q = g. One can show that every zero gives rise to a linear divisor, or more formally, if f is a polynomial in R[X] and r is an element of R such that f(r) = 0, then the polynomial (X − r) divides f. The converse is also true. The quotient can be computed using the Horner scheme
.
If F is a field
and f and g are polynomials in F[X] with g ≠ 0, then there exist unique polynomials q and r in F[X] with
and such that the degree of r is smaller than the degree of g. The polynomials q and r are uniquely determined by f and g. This is called Euclidean division, division with remainder or polynomial long division
and shows that the ring F[X] is a Euclidean domain
.
Analogously, prime polynomials (more correctly, irreducible
polynomials) can be defined as polynomials which cannot be factorized into the product of two non constant polynomials. Any polynomial may be decomposed into the product of a constant by a product of irreducible polynomials. This decomposition is unique up to the order of the factors and the multiplication of any constant factors by a constant (and division of the constant factor by the same constant. When the coefficients belong to a finite field or are rational numbers, there are algorithms to test irreducibility and to compute the factorization into irreducible polynomials. These algorithms are not practicable for hand written computation, but are available in any Computer algebra system
(see Berlekamp's algorithm
for the case in which the coefficients belong to a finite field or the Berlekamp–Zassenhaus algorithm
when working over the rational numbers ). Eisenstein's criterion
can also be used in some cases to determine irreducibility.
See also: Greatest common divisor of two polynomials
.
polynomial, a polynomial in more than one variable is called a multivariate polynomial. These notions refer more to the kind of polynomials one is generally working with than to individual polynomials; for instance when working with univariate polynomials one does not exclude constant polynomials (which may result, for instance, from the subtraction of non-constant polynomials), although strictly speaking constant polynomials do not contain any variables at all. It is possible to further classify multivariate polynomials as bivariate, trivariate, and so on, according to the maximum number of variables allowed. Again, so that the set of objects under consideration be closed under subtraction, a study of trivariate polynomials usually allows bivariate polynomials, and so on. It is common, also, to say simply "polynomials in x, y, and z", listing the variables allowed. In this case, xy is allowed.
Usually, a polynomial of degree n, for n greater than 3, is called a polynomial of degree n, although the phrases quartic polynomial and quintic polynomial are sometimes used. The use of names for degrees greater than 5 is even less common. The names for the degrees may be applied to the polynomial or to its terms. For example, in the term
the term 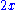 is a first degree term in a second degree polynomial.
is a first degree term in a second degree polynomial.
In the context of polynomial interpolation there is some ambiguity when combining the two classifications above. For example, a bilinear interpolant
, being the product of two univariate linear polynomials, is bivariate but is not linear; similar ambiguity affects the bicubic interpolant
.
The polynomial 0, which may be considered to have no terms at all, is called the zero polynomial. Unlike other constant polynomials, its degree is not zero. Rather the degree of the zero polynomial is either left explicitly undefined, or defined to be negative (either –1 or –∞). These conventions are important when defining Euclidean division of polynomials. The zero polynomial is also unique in that it is the only polynomial having an infinite number of roots.
If a polynomial has only one variable, then the terms are usually written either from highest degree to lowest degree ("descending powers") or from lowest degree to highest degree ("ascending powers"). A univariate polynomial in x of degree n then takes the general form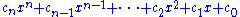
where
Here the term cnxn is called the leading term and its coefficient cn the leading coefficient; if the leading coefficient , the univariate polynomial is called monic.
Note that apart from the leading (which must be non-zero or else the polynomial would not be of degree n) this general form allows for coefficients to be zero; when this happens the corresponding term is zero and may be removed from the sum without changing the polynomial. It is nevertheless common to refer to ci as the coefficient of xi, even when ci happens to be 0, so that xi does not really occur in any term; for instance one can speak of the constant term
of the polynomial, meaning c0 even if it is zero.
In the case of polynomials in more than one variable, a polynomial is called homogeneous of if all its terms have . For example, is homogeneous.
is homogeneous.
. As in the classification by number of variables, when working with coefficients for a given set, such as the complex numbers, coefficients from any subset are allowed. Thus is a polynomial with integer coefficients, but it is also a polynomial with complex coefficients, because the integers are a subset of the complex numbers.
is a polynomial with integer coefficients, but it is also a polynomial with complex coefficients, because the integers are a subset of the complex numbers.
of a matrix or linear operator contains information about the operator's eigenvalues. The minimal polynomial
of an algebraic element
records the simplest algebraic relation satisfied by that element. The chromatic polynomial
of a graph
counts the number of proper colourings of that graph.
which studies the simultaneous zero sets of several such multivariate polynomials. These rings can alternatively be constructed by repeating the construction of univariate polynomials with as coefficient ring another ring of polynomials: thus the ring R[X,Y] of polynomials in X and Y can be viewed as the ring (R[X])[Y] of polynomials in Y with as coefficients polynomials in X, or as the ring
(R[Y])[X] of polynomials in X with as coefficients polynomials in Y. These identifications are compatible with arithmetic operations (they are isomorphism
s of rings), but some notions such as degree or whether a polynomial is considered monic can change between these points of view. One can construct rings of polynomials in infinitely many variables, but since polynomials are (finite) expressions, any individual polynomial can only contain finitely many variables.
A binary polynomial where the second variable takes the form of an exponential function applied to the first variable, for example P(X,eX ), may be called an exponential polynomial
.
Laurent polynomials are like polynomials, but allow negative powers of the variable(s) to occur.
Quotient
s of polynomials are called rational expressions (or rational fractions), and functions that evaluate rational expressions are called rational function
s. Rational fractions are formal quotients of polynomials (they are formed from polynomials just as rational number
s are formed from integer
s, writing a fraction of two of them; fractions related by the canceling of common factors are identified with each other). The rational function defined by a rational fraction is the quotient of the polynomial functions defined by the numerator and the denominator of the rational fraction. The rational fractions contain the Laurent polynomials, but do not limit denominators to be powers of a variable. While polynomial functions are defined for all values of the variables, a rational function is defined only for the values of the variables for which the denominator is not null. A rational function produces rational output for any rational input for which it is defined; this is not true of other functions such as trigonometric function
s, logarithm
s and exponential function
s.
Formal power series
are like polynomials, but allow infinitely many non-zero terms to occur, so that they do not have finite degree. Unlike polynomials they cannot in general be explicitly and fully written down (just like real number
s cannot), but the rules for manipulating their terms are the same as for polynomials.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a polynomial is an expression
Expression (mathematics)
In mathematics, an expression is a finite combination of symbols that is well-formed according to rules that depend on the context. Symbols can designate numbers , variables, operations, functions, and other mathematical symbols, as well as punctuation, symbols of grouping, and other syntactic...
of finite length constructed from variables
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
(also known as indeterminates
Indeterminate (variable)
In mathematics, and particularly in formal algebra, an indeterminate is a symbol that does not stand for anything else but itself. In particular it does not designate a constant, or a parameter of the problem, it is not an unknown that could be solved for, it is not a variable designating a...
) and constant
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s, using only the operations of addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, subtraction
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
, multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
, and non-negative integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
exponents
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
. For example, is a polynomial, but is not, because its second term
Term (mathematics)
A term is a mathematical expression which may form a separable part of an equation, a series, or another expression.-Definition:In elementary mathematics, a term is either a single number or variable, or the product of several numbers or variables separated from another term by a + or - sign in an...
involves division by the variable x (4/x) and because its third term contains an exponent that is not an integer (3/2). The term "polynomial" can also be used as an adjective, for quantities that can be expressed as a polynomial of some parameter, as in "polynomial time" which is used in computational complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
.
Polynomial comes from the Greek poly, "many" and medieval Latin binomium, "binomial
Binomial
In algebra, a binomial is a polynomial with two terms —the sum of two monomials—often bound by parenthesis or brackets when operated upon...
". The word was introduced in Latin by Franciscus Vieta.
Polynomials appear in a wide variety of areas of mathematics and science. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problems
Word problem (mathematics education)
In mathematics education, the term word problem is often used to refer to any math exercise where significant background information on the problem is presented as text rather than in mathematical notation...
to complicated problems in the sciences; they are used to define polynomial functions, which appear in settings ranging from basic chemistry
Chemistry
Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
to economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
and social science; they are used in calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
and numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
to approximate other functions. In advanced mathematics, polynomials are used to construct polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
s, a central concept in abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
.
Overview
A polynomial is either zero, or can be written as the sum of one or more non-zero termsTerm (mathematics)
A term is a mathematical expression which may form a separable part of an equation, a series, or another expression.-Definition:In elementary mathematics, a term is either a single number or variable, or the product of several numbers or variables separated from another term by a + or - sign in an...
. The number of terms is finite. These terms consist of a constant (called the coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
of the term) which may be multiplied by a finite number of variables
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
(usually represented by letters), also called indeterminates
Indeterminate (variable)
In mathematics, and particularly in formal algebra, an indeterminate is a symbol that does not stand for anything else but itself. In particular it does not designate a constant, or a parameter of the problem, it is not an unknown that could be solved for, it is not a variable designating a...
. Each variable may have an exponent that is a non-negative integer, i.e., a natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
. The exponent on a variable in a term is called the degree
Degree of a polynomial
The degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...
of that variable in that term, the degree of the term is the sum of the degrees of the variables in that term, and the degree of a polynomial is the largest degree of any one term. Since , the degree of a variable without a written exponent is one. A term with no variables is called a constant term
Constant term
In mathematics, a constant term is a term in an algebraic expression has a value that is constant or cannot change, because it does not contain any modifiable variables. For example, in the quadratic polynomialx^2 + 2x + 3,\ the 3 is a constant term....
, or just a constant. The degree of a (nonzero) constant term is 0. The coefficient of a term may be any number from a specified set. If that set is the set of real numbers, we speak of "polynomials over the reals". Other common kinds of polynomials are polynomials with integer coefficients, polynomials with complex coefficients, and polynomials with coefficients that are integers modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
of some prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p. In most of the examples in this section, the coefficients are integers.
For example:
is a term. The coefficient is –5, the variables are x and y, the degree of x is in the term two, while the degree of y is one.
The degree of the entire term is the sum of the degrees of each variable in it, so in this example the degree is 2 + 1 = 3.
Forming a sum of several terms produces a polynomial. For example, the following is a polynomial:

It consists of three terms: the first is degree two, the second is degree one, and the third is degree zero.
The commutative law of addition can be used to freely permute terms into any preferred order.
In polynomials with one variable, the terms are usually ordered according to degree, either in "descending powers of x", with the term of largest degree first, or in "ascending powers of x". The polynomial in the example above is written in descending powers of x. The first term has coefficient 3, variable x, and exponent 2. In the second term, the coefficient . The third term is a constant. Since the degree of a non-zero polynomial is the largest degree of any one term, this polynomial has degree two.
Two terms with the same variables raised to the same powers are called "like terms", and they can be combined (after having been made adjacent) using the distributive law into a single term, whose coefficient is the sum of the coefficients of the terms that were combined. It may happen that this makes the coefficient 0, in which case their combination just cancels out the terms. Polynomials can be added using the associative law of addition (which simply groups all their terms together into a single sum), possibly followed by reordering, and combining of like terms. For example, if


then

which can be simplified to

To work out the product of two polynomials into a sum of terms, the distributive law is repeatedly applied, with as result that each term of one polynomial multiplied by every term of the other. For example, if

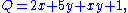
then

which can be simplified to

The sum or product of two polynomials is always a polynomial.
Alternative forms
In general any expression can be considered to be a polynomial if it is built up from variables and constants using only additionAddition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, subtraction
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
, multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
, and raising expressions to constant positive whole number power
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
s. Such an expression can always be rewritten as a sum of terms. For example, (x + 1)3 is a polynomial; its standard form is x3 + 3x2 + 3x + 1.
Division of one polynomial by another does not, in general, produce a polynomial, but rather produces a quotient and a remainder. A formal quotient of polynomials, that is, an algebraic fraction where the numerator and denominator are polynomials, is called a "rational expression
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
" or "rational fraction" and is not, in general, a polynomial. Division of a polynomial by a number, however, does yield another polynomial. For example,
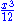
is considered a valid term in a polynomial (and a polynomial by itself) because it is equivalent to
 and
and  is just a constant. When this expression is used as a term, its coefficient is therefore
is just a constant. When this expression is used as a term, its coefficient is therefore  . For similar reasons, if complex coefficients are allowed, one may have a single term like
. For similar reasons, if complex coefficients are allowed, one may have a single term like  ; even though it looks like it should be expanded to two terms, the complex number 2 + 3i is one complex number, and is the coefficient of that term.
; even though it looks like it should be expanded to two terms, the complex number 2 + 3i is one complex number, and is the coefficient of that term.is not a polynomial because it includes division by a non-constant polynomial.
is not a polynomial, because it contains a variable used as exponent.
Since subtraction can be replaced by addition of the opposite quantity, and since positive whole number exponents can be replaced by repeated multiplication, all polynomials can be constructed from constants and variables using only addition and multiplication.
Polynomial functions
A polynomial function is a function that can be defined by evaluatingExpression (mathematics)
In mathematics, an expression is a finite combination of symbols that is well-formed according to rules that depend on the context. Symbols can designate numbers , variables, operations, functions, and other mathematical symbols, as well as punctuation, symbols of grouping, and other syntactic...
a polynomial. A function ƒ of one argument
Argument of a function
In mathematics, an argument of a function is a specific input in the function, also known as an independent variable. When it is clear from the context which argument is meant, the argument is often denoted by arg....
is called a polynomial function if it satisfies
for all arguments x, where n is a non-negative integer and a0, a1,a2, ..., an are constant coefficients.
For example, the function ƒ, taking real numbers to real numbers, defined by

is a polynomial function of one argument. Polynomial functions of multiple arguments can also be defined, using polynomials in multiple variables, as in
An example is also the function
 which, although it doesn't look like a polynomial, is a polynomial function since for every x it is true that
which, although it doesn't look like a polynomial, is a polynomial function since for every x it is true that 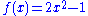 (see Chebyshev polynomials
(see Chebyshev polynomialsChebyshev polynomials
In mathematics the Chebyshev polynomials, named after Pafnuty Chebyshev, are a sequence of orthogonal polynomials which are related to de Moivre's formula and which can be defined recursively. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and...
).
Polynomial functions are a class of functions having many important properties. They are all continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
, entire
Entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
, computable
Computable function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
, etc.
Polynomial equations
A polynomial equation, also called algebraic equation, is an equationEquation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
in which a polynomial is set equal to another polynomial.
is a polynomial equation. In case of a univariate polynomial equation, the variable is considered an unknown
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
, and one seeks to find the possible values for which both members of the equation evaluate to the same value (in general more than one solution may exist). A polynomial equation is to be contrasted with a polynomial identity like , where both members represent the same polynomial in different forms, and as a consequence any evaluation of both members will give a valid equality. This means that a polynomial identity is a polynomial equation for which all possible values of the unknowns are solutions.
Elementary properties of polynomials
- A sumSUMSUM can refer to:* The State University of Management* Soccer United Marketing* Society for the Establishment of Useful Manufactures* StartUp-Manager* Software User’s Manual,as from DOD-STD-2 167A, and MIL-STD-498...
of polynomials is a polynomial. - A productProduct (mathematics)In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
of polynomials is a polynomial. - A compositionFunction compositionIn mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
of two polynomials is a polynomial, which is obtained by substituting a variable of the first polynomial by the second polynomial. - The derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the polynomial anxn + an-1xn-1 + ... + a2x2 + a1x + a0 is the polynomial nanxn-1 + (n-1)an-1xn-2 + ... + 2a2x + a1. If the set of the coefficients does not contain the integers (for example if the coefficients are integers moduloModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
some prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p), then kak should be interpreted as the sum of ak with itself, k times. For example, over the integers modulo p, the derivative of the polynomial xp+1 is the polynomial 0. - If the division by integers is allowed in the set of coefficients, a primitive or antiderivativeAntiderivativeIn calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
of the polynomial anxn + an-1xn-1 + ... + a2x2 + a1x + a0 is anxn+1/(n+1) + an-1xn/n + ... + a2x3/3 + a1x2/2 + a0x +c, where c is an arbitrary constant. Thus x2+1 is a polynomial with integer coefficients whose primitives are not polynomials over the integers. If this polynomial is viewed as a polynomial over the integers modulo 3 it has no primitive at all.
Polynomials serve to approximate other functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, such as sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
, cosine, and exponential
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
.
All polynomials have an expanded form, in which the distributive and associative laws have been used to remove all brackets and commutative law has been used to make the like terms adjacent and combine them. All polynomials with coefficients in a unique factorization domain
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
(for example, the integers or a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
also have a factored form in which the polynomial is written as a product of irreducible polynomial
Irreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
s and a constant. In the case of the field of complex numbers, the irreducible polynomials are linear.
For example, the factored form of
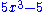
is
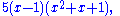
over the integers and
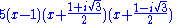
over the complex numbers.
Every polynomial in one variable is equivalent to a polynomial with the form

This form is sometimes taken as the definition of a polynomial in one variable.
Evaluation of a polynomial consists of assigning a number to each variable and carrying out the indicated multiplications and additions. Actual evaluation is usually more efficient using the Horner scheme
Horner scheme
In numerical analysis, the Horner scheme , named after William George Horner, is an algorithm for the efficient evaluation of polynomials in monomial form. Horner's method describes a manual process by which one may approximate the roots of a polynomial equation...
:

In elementary algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, methods are given for solving all first degree and second degree polynomial equations in one variable. In the case of polynomial equations, the variable is often called an unknown. The number of solutions may not exceed the degree, and will equal the degree when multiplicity
Multiplicity (mathematics)
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
of solutions and complex number solutions are counted. This fact is called the fundamental theorem of algebra.
A system of polynomial equations is a set of equations in which each variable must take on the same value everywhere it appears in any of the equations. Systems of equations are usually grouped with a single open brace on the left. In elementary algebra
Elementary algebra
Elementary algebra is a fundamental and relatively basic form of algebra taught to students who are presumed to have little or no formal knowledge of mathematics beyond arithmetic. It is typically taught in secondary school under the term algebra. The major difference between algebra and...
, in particular in linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, methods are given for solving a system of linear equations in several unknowns. If there are more unknowns than equations, the system is called underdetermined. If there are more equations than unknowns, the system is called overdetermined
Overdetermined system
In mathematics, a system of linear equations is considered overdetermined if there are more equations than unknowns. The terminology can be described in terms of the concept of counting constraints. Each unknown can be seen as an available degree of freedom...
. Overdetermined systems are common in practical applications. For example, one U.S. mapping survey used computers to solve 2.5 million equations in 400,000 unknowns.
Viète's formulas relate the coefficients of a polynomial to symmetric polynomial
Symmetric polynomial
In mathematics, a symmetric polynomial is a polynomial P in n variables, such that if any of the variables are interchanged, one obtains the same polynomial...
functions of its roots.
History
Determining the roots of polynomials, or "solving algebraic equations", is among the oldest problems in mathematics. However, the elegant and practical notation we use today only developed beginning in the 15th century. Before that, equations were written out in words. For example, an algebra problem from the Chinese Arithmetic in Nine SectionsThe Nine Chapters on the Mathematical Art
The Nine Chapters on the Mathematical Art is a Chinese mathematics book, composed by several generations of scholars from the 10th–2nd century BCE, its latest stage being from the 1st century CE...
, circa 200 BCE, begins "Three sheafs of good crop, two sheafs of mediocre crop, and one sheaf of bad crop are sold for 29 dou." We would write 3x + 2y + z = 29.
Notation
The earliest known use of the equal sign is in Robert RecordeRobert Recorde
Robert Recorde was a Welsh physician and mathematician. He introduced the "equals" sign in 1557.-Biography:A member of a respectable family of Tenby, Wales, he entered the University of Oxford about 1525, and was elected a fellow of All Souls College in 1531...
's The Whetstone of Witte, 1557. The signs + for addition, − for subtraction, and the use of a letter for an unknown appear in Michael Stifel
Michael Stifel
Michael Stifel or Styfel was a German monk and mathematician. He was an Augustinian who became an early supporter of Martin Luther. Stifel was later appointed professor of mathematics at Jena University...
's Arithemetica integra, 1544. René Descartes
René Descartes
René Descartes ; was a French philosopher and writer who spent most of his adult life in the Dutch Republic. He has been dubbed the 'Father of Modern Philosophy', and much subsequent Western philosophy is a response to his writings, which are studied closely to this day...
, in La géometrie, 1637, introduced the concept of the graph of a polynomial equation. He popularized the use of letters from the beginning of the alphabet to denote constants and letters from the end of the alphabet to denote variables, as can be seen above, in the general formula for a polynomial in one variable, where the a 's denote constants and x denotes a variable. Descartes introduced the use of superscripts to denote exponents as well.
Solving polynomial equations
Every polynomial P in x corresponds to a function, ƒ(x) = P (where the occurrences of x in P are interpreted as the argument of ƒ), called the polynomial function of P; the equation in x setting f(x) = 0 is the polynomial equation corresponding to P. The solutions of this equation are called the roots of the polynomial; they are the zeroes of the function ƒ (corresponding to the points where the graph of ƒ meets the x-axis). A number a is a root of P if and only if the polynomial x − a (of degree one in x) divides P. It may happen that x − a divides P more than once: if (x − a)2 divides P then a is called a multiple root of P, and otherwise a is called a simple root of P. If P is a nonzero polynomial, there is a highest power m such that (x − a)m divides P, which is called the multiplicity of the root a in P. When P is the zero polynomial, the corresponding polynomial equation is trivial, and this case is usually excluded when considering roots: with the above definitions every number would be a root of the zero polynomial, with undefined (or infinite) multiplicity. With this exception made, the number of roots of P, even counted with their respective multiplicities, cannot exceed the degree of P.Some polynomials, such as x2 + 1, do not have any roots among the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. If, however, the set of allowed candidates is expanded to the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, every non-constant polynomial has at least one root; this is the fundamental theorem of algebra
Fundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
. By successively dividing out factors x − a, one sees that any polynomial with complex coefficients can be written as a constant (its leading coefficient) times a product of such polynomial factors of degree 1; as a consequence the number of (complex) roots counted with their multiplicities is exactly equal to the degree of the polynomial.
There is a difference between approximating roots and finding exact expressions for roots. Formulas for expressing the roots of polynomials of degree 2 in terms of square roots have been known since ancient times (see quadratic equation
Quadratic equation
In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
), and for polynomials of degree 3 or 4 similar formulas (using cube roots in addition to square roots) were found in the 16th century (see cubic function
Cubic function
In mathematics, a cubic function is a function of the formf=ax^3+bx^2+cx+d,\,where a is nonzero; or in other words, a polynomial of degree three. The derivative of a cubic function is a quadratic function...
and quartic function
Quartic function
In mathematics, a quartic function, or equation of the fourth degree, is a function of the formf=ax^4+bx^3+cx^2+dx+e \,where a is nonzero; or in other words, a polynomial of degree four...
for the formulas and Niccolo Fontana Tartaglia
Niccolò Fontana Tartaglia
Niccolò Fontana Tartaglia was a mathematician, an engineer , a surveyor and a bookkeeper from the then-Republic of Venice...
, Lodovico Ferrari
Lodovico Ferrari
Lodovico Ferrari was an Italian mathematician.Born in Milan, Italy, grandfather, Bartholomew Ferrari was forced out of Milan to Bologna. He settled in Bologna, Italy and he began his career as the servant of Gerolamo Cardano. He was extremely bright, so Cardano started teaching him mathematics...
, Gerolamo Cardano
Gerolamo Cardano
Gerolamo Cardano was an Italian Renaissance mathematician, physician, astrologer and gambler...
, and Vieta for historical details). But formulas for degree 5 eluded researchers. In 1824, Niels Henrik Abel
Niels Henrik Abel
Niels Henrik Abel was a Norwegian mathematician who proved the impossibility of solving the quintic equation in radicals.-Early life:...
proved the striking result that there can be no general (finite) formula, involving only arithmetic operations and radicals, that expresses the roots of a polynomial of degree 5 or greater in terms of its coefficients (see Abel-Ruffini theorem). In 1830, Évariste Galois
Évariste Galois
Évariste Galois was a French mathematician born in Bourg-la-Reine. While still in his teens, he was able to determine a necessary and sufficient condition for a polynomial to be solvable by radicals, thereby solving a long-standing problem...
, studying the permutations of the roots of a polynomial, extended Abel-Ruffini theorem by showing that, given a polynomial equation, one may decide if it is solvable by radicals, and, if it is, solve it. This result marked the start of Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
and Group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, two important branches of modern mathematics. Galois himself noted that the computations implied by his method were impracticable. Nevertheless formulas for solvable equations of degrees 5 and 6 have been published (see quintic function and sextic equation
Sextic equation
In mathematics, a sextic equation is a polynomial equation of degree six. It is of the form:ax^6+bx^5+cx^4+dx^3+ex^2+fx+g=0,\,where a \neq 0....
).
Numerical approximations of roots of polynomial equations in one unknown is easily done on a computer by the Jenkins-Traub method, Laguerre's method
Laguerre's method
In numerical analysis, Laguerre's method is a root-finding algorithm tailored to polynomials. In other words, Laguerre's method can be used to solve numerically the equation\ p = 0 for a given polynomial p...
, Durand–Kerner method or by some other root-finding algorithm
Root-finding algorithm
A root-finding algorithm is a numerical method, or algorithm, for finding a value x such that f = 0, for a given function f. Such an x is called a root of the function f....
.
For polynomials in more than one variable the notion of root does not exist, and there are usually infinitely many combinations of values for the variables for which the polynomial function takes the value zero. However for certain sets of such polynomials it may happen that for only finitely many combinations all polynomial functions take the value zero.
For a set of polynomial equations in several unknowns, there are algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s to decide if they have a finite number of complex solutions. If the number of solutions is finite, there are algorithms to compute the solutions. The methods underlying these algorithms are described in the article systems of polynomial equations
Systems of polynomial equations
A system of polynomial equations is a set of simultaneous equations f1 = 0, ..., fh = 0 where the fi are polynomials in several variables, say x1, ..., xn, over some field k....
.
The special case where all the polynomials are of degree one is called a system of linear equations, for which another range of different solution methods exist, including the classical Gaussian elimination
Gaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
.
It has been shown by Richard Birkeland and Karl Meyr that the roots of any polynomial may be expressed in terms of multivariate hypergeometric functions. Ferdinand von Lindemann
Ferdinand von Lindemann
Carl Louis Ferdinand von Lindemann was a German mathematician, noted for his proof, published in 1882, that π is a transcendental number, i.e., it is not a root of any polynomial with rational coefficients....
and Hiroshi Umemura showed that the roots may also be expressed in terms of Siegel modular functions, generalizations of the theta functions that appear in the theory of elliptic function
Elliptic function
In complex analysis, an elliptic function is a function defined on the complex plane that is periodic in two directions and at the same time is meromorphic...
s. These characterisations of the roots of arbitrary polynomials are generalisations of the methods previously discovered to solve the quintic equation
Quintic equation
In mathematics, a quintic function is a function of the formg=ax^5+bx^4+cx^3+dx^2+ex+f,\,where a, b, c, d, e and f are members of a field, typically the rational numbers, the real numbers or the complex numbers, and a is nonzero...
.
Method based on eigenvalues computation
A numerical method for the progressive elimination of multiple roots, based on eigenvalue computation, has been proposed. The method transforms the problem into a sequence of eigenvalue problems involving tridiagonal matrices with only simple eigenvalues: such eigenvalues can easily be approximated by means of the QR algorithmQR algorithm
In numerical linear algebra, the QR algorithm is an eigenvalue algorithm: that is, a procedure to calculate the eigenvalues and eigenvectors of a matrix. The QR transformation was developed in the late 1950s by John G.F. Francis and by Vera N. Kublanovskaya , working independently...
.
Graphs
A polynomial function in one real variable can be represented by a graphGraph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
.
- The graph of the zero polynomial
-
- f(x) = 0
- is the x-axis.
- The graph of a degree 0 polynomial
-
- f(x) = a0, where a0 ≠ 0,
- is a horizontal line with y-intercept a0
- The graph of a degree 1 polynomial (or linear function)
-
- f(x) = a0 + a1x , where a1 ≠ 0,
- is an oblique line with y-intercept a0 and slopeSlopeIn mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
a1.
- The graph of a degree 2 polynomial
-
- f(x) = a0 + a1x + a2x2, where a2 ≠ 0
- is a parabolaParabolaIn mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
.
- The graph of a degree 3 polynomial
-
- f(x) = a0 + a1x + a2x2, + a3x3, where a3 ≠ 0
- is a cubic curve.
- The graph of any polynomial with degree 2 or greater
-
- f(x) = a0 + a1x + a2x2 + ... + anxn , where an ≠ 0 and n ≥ 2
- is a continuous non-linear curve.
The graph of a non-constant (univariate) polynomial always tends to infinity when the variable increases indefinitely (in absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
).
Polynomial graphs are analyzed in calculus using intercepts, slopes, concavity, and end behavior.
The illustrations below show graphs of polynomials.
Polynomials and calculus
One important aspect of calculus is the project of analyzing complicated functions by means of approximating them with polynomial functions. The culmination of these efforts is Taylor's theoremTaylor's theorem
In calculus, Taylor's theorem gives an approximation of a k times differentiable function around a given point by a k-th order Taylor-polynomial. For analytic functions the Taylor polynomials at a given point are finite order truncations of its Taylor's series, which completely determines the...
, which roughly states that every differentiable function locally looks like a polynomial function, and the Stone-Weierstrass theorem
Stone-Weierstrass theorem
In mathematical analysis, the Weierstrass approximation theorem states that every continuous function defined on an interval [a,b] can be uniformly approximated as closely as desired by a polynomial function...
, which states that every continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
defined on a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
of the real axis can be approximated on the whole interval as closely as desired by a polynomial function. Polynomial functions are also frequently used to interpolate
Polynomial interpolation
In numerical analysis, polynomial interpolation is the interpolation of a given data set by a polynomial: given some points, find a polynomial which goes exactly through these points.- Applications :...
functions.
Calculating derivatives and integrals of polynomial functions is particularly simple. For the polynomial function

the derivative with respect to x is
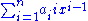
and the indefinite integral is

Abstract algebra
In abstract algebraAbstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, one distinguishes between polynomials and polynomial functions. A polynomial f in one variable X over a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R is defined to be a formal expression of the form
where n is a natural number, the coefficients
 are elements of R, and X is a formal symbol, whose powers Xi are just placeholders for the corresponding coefficients ai, so that the given formal expression is just a way to encode the sequence
are elements of R, and X is a formal symbol, whose powers Xi are just placeholders for the corresponding coefficients ai, so that the given formal expression is just a way to encode the sequence 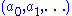 , where there is an n such that ai = 0 for all i > n. Two polynomials sharing the same value of n are considered to be equal if and only if the sequences of their coefficients are equal; furthermore any polynomial is equal to any polynomial with greater value of n obtained from it by adding terms in front whose coefficient is zero. These polynomials can be added by simply adding corresponding coefficients (the rule for extending by terms with zero coefficients can be used to make sure such coefficients exist). Thus each polynomial is actually equal to the sum of the terms used in its formal expression, if such a term aiXi is interpreted as a polynomial that has zero coefficients at all powers of X other than Xi. Then to define multiplication, it suffices by the distributive law to describe the product of any two such terms, which is given by the rule
, where there is an n such that ai = 0 for all i > n. Two polynomials sharing the same value of n are considered to be equal if and only if the sequences of their coefficients are equal; furthermore any polynomial is equal to any polynomial with greater value of n obtained from it by adding terms in front whose coefficient is zero. These polynomials can be added by simply adding corresponding coefficients (the rule for extending by terms with zero coefficients can be used to make sure such coefficients exist). Thus each polynomial is actually equal to the sum of the terms used in its formal expression, if such a term aiXi is interpreted as a polynomial that has zero coefficients at all powers of X other than Xi. Then to define multiplication, it suffices by the distributive law to describe the product of any two such terms, which is given by the rule- for all elements a, b of the ring R and all natural numbers k and l.
Thus the set of all polynomials with coefficients in the ring R forms itself a ring, the ring of polynomials over R, which is denoted by R[X]. The map from R to R[X] sending r to rX0 is an injective homomorphism of rings, by which R is viewed as a subring of R[X]. If R is commutative
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
, then R[X] is an algebra
Algebra (ring theory)
In mathematics, specifically in ring theory, an algebra over a commutative ring is a generalization of the concept of an algebra over a field, where the base field K is replaced by a commutative ring R....
over R.
One can think of the ring R[X] as arising from R by adding one new element X to R, and extending in a minimal way to a ring in which X satisfies no other relations than the obligatory ones, plus commutation with all elements of R (that is ). To do this, one must add all powers of X and their linear combinations as well.
Formation of the polynomial ring, together with forming factor rings by factoring out ideals
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
, are important tools for constructing new rings out of known ones. For instance, the ring (in fact field) of complex numbers, which can be constructed from the polynomial ring R[X] over the real numbers by factoring out the ideal of multiples of the polynomial . Another example is the construction of finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s, which proceeds similarly, starting out with the field of integers modulo some prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
as the coefficient ring R (see modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
).
If R is commutative, then one can associate to every polynomial P in R[X], a polynomial function f with domain and range equal to R (more generally one can take domain and range to be the same unital associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
over R). One obtains the value f(r) by substitution
Substitution (algebra)
In algebra, the operation of substitution can be applied in various contexts involving formal objects containing symbols ; the operation consists of systematically replacing occurrences of some symbol by a given value.A common case of substitution involves polynomials, where substitution of a...
of the value r for the symbol X in P. One reason to distinguish between polynomials and polynomial functions is that over some rings different polynomials may give rise to the same polynomial function (see Fermat's little theorem
Fermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
for an example where R is the integers modulo p). This is not the case when R is the real or complex numbers, whence the two concepts are not always distinguished in analysis. An even more important reason to distinguish between polynomials and polynomial functions is that many operations on polynomials (like Euclidean division) require looking at what a polynomial is composed of as an expression rather than evaluating it at some constant value for X. And it should be noted that if R is not commutative, there is no (well behaved) notion of polynomial function at all.
Divisibility
In commutative algebraCommutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, one major focus of study is divisibility among polynomials. If R is an integral domain and f and g are polynomials in R[X], it is said that f divides g or f is a divisor of g if there exists a polynomial q in R[X] such that f q = g. One can show that every zero gives rise to a linear divisor, or more formally, if f is a polynomial in R[X] and r is an element of R such that f(r) = 0, then the polynomial (X − r) divides f. The converse is also true. The quotient can be computed using the Horner scheme
Horner scheme
In numerical analysis, the Horner scheme , named after William George Horner, is an algorithm for the efficient evaluation of polynomials in monomial form. Horner's method describes a manual process by which one may approximate the roots of a polynomial equation...
.
If F is a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
and f and g are polynomials in F[X] with g ≠ 0, then there exist unique polynomials q and r in F[X] with

and such that the degree of r is smaller than the degree of g. The polynomials q and r are uniquely determined by f and g. This is called Euclidean division, division with remainder or polynomial long division
Polynomial long division
In algebra, polynomial long division is an algorithm for dividing a polynomial by another polynomial of the same or lower degree, a generalised version of the familiar arithmetic technique called long division...
and shows that the ring F[X] is a Euclidean domain
Euclidean domain
In mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
.
Analogously, prime polynomials (more correctly, irreducible
Irreducible element
In abstract algebra, a non-zero non-unit element in an integral domain is said to be irreducible if it is not a product of two non-units.Irreducible elements should not be confused with prime elements...
polynomials) can be defined as polynomials which cannot be factorized into the product of two non constant polynomials. Any polynomial may be decomposed into the product of a constant by a product of irreducible polynomials. This decomposition is unique up to the order of the factors and the multiplication of any constant factors by a constant (and division of the constant factor by the same constant. When the coefficients belong to a finite field or are rational numbers, there are algorithms to test irreducibility and to compute the factorization into irreducible polynomials. These algorithms are not practicable for hand written computation, but are available in any Computer algebra system
Computer algebra system
A computer algebra system is a software program that facilitates symbolic mathematics. The core functionality of a CAS is manipulation of mathematical expressions in symbolic form.-Symbolic manipulations:...
(see Berlekamp's algorithm
Berlekamp's algorithm
In mathematics, particularly computational algebra, Berlekamp's algorithm is a well-known method for factoring polynomials over finite fields . The algorithm consists mainly of matrix reduction and polynomial GCD computations. It was invented by Elwyn Berlekamp in 1967...
for the case in which the coefficients belong to a finite field or the Berlekamp–Zassenhaus algorithm
Berlekamp–Zassenhaus algorithm
In mathematics, in particular in computational algebra, the Berlekamp–Zassenhaus algorithm is an algorithm for factoring polynomials over the integers. As a consequence of Gauss's lemma, this amounts to solving the problem also over the rationals...
when working over the rational numbers ). Eisenstein's criterion
Eisenstein's criterion
In mathematics, Eisenstein's criterion gives an easily checked sufficient condition for a polynomial with integer coefficients to be irreducible over the rational numbers...
can also be used in some cases to determine irreducibility.
See also: Greatest common divisor of two polynomials
Greatest common divisor of two polynomials
Informally, the greatest common divisor of two polynomials p and q is the largest polynomial that divides both p and q evenly. The definition is modeled on the concept of the greatest common divisor of two integers, the greatest integer that divides both...
.
Number of variables
One classification of polynomials is based on the number of distinct variables. A polynomial in one variable is called a univariateUnivariate
In mathematics, univariate refers to an expression, equation, function or polynomial of only one variable. Objects of any of these types but involving more than one variable may be called multivariate...
polynomial, a polynomial in more than one variable is called a multivariate polynomial. These notions refer more to the kind of polynomials one is generally working with than to individual polynomials; for instance when working with univariate polynomials one does not exclude constant polynomials (which may result, for instance, from the subtraction of non-constant polynomials), although strictly speaking constant polynomials do not contain any variables at all. It is possible to further classify multivariate polynomials as bivariate, trivariate, and so on, according to the maximum number of variables allowed. Again, so that the set of objects under consideration be closed under subtraction, a study of trivariate polynomials usually allows bivariate polynomials, and so on. It is common, also, to say simply "polynomials in x, y, and z", listing the variables allowed. In this case, xy is allowed.
Degree
A second major way of classifying polynomials is by their degree. Recall that the degree of a term is the sum of the exponents on variables, and that the degree of a polynomial is the largest degree of any one term.| Degree | Name | Example |
|---|---|---|
| −∞ | zero |  |
 |
(non-zero) constant Constant function In mathematics, a constant function is a function whose values do not vary and thus are constant. For example the function f = 4 is constant since f maps any value to 4... |
 |
 |
linear Linear equation A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable.... |
 |
 |
quadratic Quadratic function A quadratic function, in mathematics, is a polynomial function of the formf=ax^2+bx+c,\quad a \ne 0.The graph of a quadratic function is a parabola whose axis of symmetry is parallel to the y-axis.... |
 |
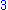 |
cubic Cubic function In mathematics, a cubic function is a function of the formf=ax^3+bx^2+cx+d,\,where a is nonzero; or in other words, a polynomial of degree three. The derivative of a cubic function is a quadratic function... |
 |
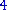 |
quartic Quartic function In mathematics, a quartic function, or equation of the fourth degree, is a function of the formf=ax^4+bx^3+cx^2+dx+e \,where a is nonzero; or in other words, a polynomial of degree four... (or biquadratic) |
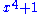 |
 |
quintic Quintic equation In mathematics, a quintic function is a function of the formg=ax^5+bx^4+cx^3+dx^2+ex+f,\,where a, b, c, d, e and f are members of a field, typically the rational numbers, the real numbers or the complex numbers, and a is nonzero... |
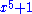 |
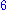 |
sextic Sextic equation In mathematics, a sextic equation is a polynomial equation of degree six. It is of the form:ax^6+bx^5+cx^4+dx^3+ex^2+fx+g=0,\,where a \neq 0.... (or hexic) |
 |
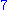 |
septic Septic equation In mathematics, a septic equation, heptic equation or septimic equation is a polynomial equation of degree seven. It is of the form:ax^7+bx^6+cx^5+dx^4+ex^3+fx^2+gx+h=0,\,... (or heptic) |
 |
 |
octic |  |
 |
nonic |  |
 |
decic |  |
 |
hectic |  |
Usually, a polynomial of degree n, for n greater than 3, is called a polynomial of degree n, although the phrases quartic polynomial and quintic polynomial are sometimes used. The use of names for degrees greater than 5 is even less common. The names for the degrees may be applied to the polynomial or to its terms. For example, in
 the term
the term 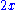 is a first degree term in a second degree polynomial.
is a first degree term in a second degree polynomial.In the context of polynomial interpolation there is some ambiguity when combining the two classifications above. For example, a bilinear interpolant
Bilinear interpolation
In mathematics, bilinear interpolation is an extension of linear interpolation for interpolating functions of two variables on a regular grid. The interpolated function should not use the term of x^2 or y^2, but x y, which is the bilinear form of x and y.The key idea is to perform linear...
, being the product of two univariate linear polynomials, is bivariate but is not linear; similar ambiguity affects the bicubic interpolant
Bicubic interpolation
In mathematics, bicubic interpolation is an extension of cubic interpolation for interpolating data points on a two dimensional regular grid. The interpolated surface is smoother than corresponding surfaces obtained by bilinear interpolation or nearest-neighbor interpolation...
.
The polynomial 0, which may be considered to have no terms at all, is called the zero polynomial. Unlike other constant polynomials, its degree is not zero. Rather the degree of the zero polynomial is either left explicitly undefined, or defined to be negative (either –1 or –∞). These conventions are important when defining Euclidean division of polynomials. The zero polynomial is also unique in that it is the only polynomial having an infinite number of roots.
| Number of non-zero terms | Name | Example |
|---|---|---|
 |
zero polynomial |  |
 |
monomial | 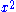 |
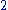 |
binomial |  |
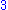 |
trinomial |  |
If a polynomial has only one variable, then the terms are usually written either from highest degree to lowest degree ("descending powers") or from lowest degree to highest degree ("ascending powers"). A univariate polynomial in x of degree n then takes the general form
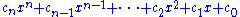
where
- cn ≠ 0, cn-1, ..., c2, c1 and c0 are constants, the coefficients of this polynomial.
Here the term cnxn is called the leading term and its coefficient cn the leading coefficient; if the leading coefficient , the univariate polynomial is called monic.
Note that apart from the leading (which must be non-zero or else the polynomial would not be of degree n) this general form allows for coefficients to be zero; when this happens the corresponding term is zero and may be removed from the sum without changing the polynomial. It is nevertheless common to refer to ci as the coefficient of xi, even when ci happens to be 0, so that xi does not really occur in any term; for instance one can speak of the constant term
Constant term
In mathematics, a constant term is a term in an algebraic expression has a value that is constant or cannot change, because it does not contain any modifiable variables. For example, in the quadratic polynomialx^2 + 2x + 3,\ the 3 is a constant term....
of the polynomial, meaning c0 even if it is zero.
In the case of polynomials in more than one variable, a polynomial is called homogeneous of if all its terms have . For example,
 is homogeneous.
is homogeneous.Coefficients
Another classification of polynomials is by the kind of constant values allowed as coefficients. One can work with polynomials with integer, rational, real, or complex coefficients, and in abstract algebra polynomials with many other types of coefficients can be defined, such as integers modulo pModular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
. As in the classification by number of variables, when working with coefficients for a given set, such as the complex numbers, coefficients from any subset are allowed. Thus
 is a polynomial with integer coefficients, but it is also a polynomial with complex coefficients, because the integers are a subset of the complex numbers.
is a polynomial with integer coefficients, but it is also a polynomial with complex coefficients, because the integers are a subset of the complex numbers.Number of non-zero terms
Polynomials may also be classified by the number of terms with nonzero coefficients, so that a one-term polynomial is called a monomial, a two-term polynomial is called a binomial, and so on. (Some authors use "monomial" to mean "monic monomial".)Polynomials associated to other objects
Polynomials are frequently used to encode information about some other object. The characteristic polynomialCharacteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of a matrix or linear operator contains information about the operator's eigenvalues. The minimal polynomial
Minimal polynomial (field theory)
In field theory, given a field extension E / F and an element α of E that is an algebraic element over F, the minimal polynomial of α is the monic polynomial p, with coefficients in F, of least degree such that p = 0...
of an algebraic element
Algebraic element
In mathematics, if L is a field extension of K, then an element a of L is called an algebraic element over K, or just algebraic over K, if there exists some non-zero polynomial g with coefficients in K such that g=0...
records the simplest algebraic relation satisfied by that element. The chromatic polynomial
Chromatic polynomial
The chromatic polynomial is a polynomial studied in algebraic graph theory, a branch of mathematics. It counts the number of graph colorings as a function of the number of colors and was originally defined by George David Birkhoff to attack the four color problem. It was generalised to the Tutte...
of a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
counts the number of proper colourings of that graph.
Extensions of the concept of a polynomial
Polynomials can involve more than one variable, in which they are called multivariate. Rings of polynomials in a finite number of variables are of fundamental importance in algebraic geometryAlgebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
which studies the simultaneous zero sets of several such multivariate polynomials. These rings can alternatively be constructed by repeating the construction of univariate polynomials with as coefficient ring another ring of polynomials: thus the ring R[X,Y] of polynomials in X and Y can be viewed as the ring (R[X])[Y] of polynomials in Y with as coefficients polynomials in X, or as the ring
(R[Y])[X] of polynomials in X with as coefficients polynomials in Y. These identifications are compatible with arithmetic operations (they are isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
s of rings), but some notions such as degree or whether a polynomial is considered monic can change between these points of view. One can construct rings of polynomials in infinitely many variables, but since polynomials are (finite) expressions, any individual polynomial can only contain finitely many variables.
A binary polynomial where the second variable takes the form of an exponential function applied to the first variable, for example P(X,eX ), may be called an exponential polynomial
Exponential polynomial
In mathematics, exponential polynomials are functions on fields, rings, or abelian groups that take the form of polynomials in a variable and an exponential function.-In fields:...
.
Laurent polynomials are like polynomials, but allow negative powers of the variable(s) to occur.
Quotient
Quotient
In mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
s of polynomials are called rational expressions (or rational fractions), and functions that evaluate rational expressions are called rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s. Rational fractions are formal quotients of polynomials (they are formed from polynomials just as rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s are formed from integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, writing a fraction of two of them; fractions related by the canceling of common factors are identified with each other). The rational function defined by a rational fraction is the quotient of the polynomial functions defined by the numerator and the denominator of the rational fraction. The rational fractions contain the Laurent polynomials, but do not limit denominators to be powers of a variable. While polynomial functions are defined for all values of the variables, a rational function is defined only for the values of the variables for which the denominator is not null. A rational function produces rational output for any rational input for which it is defined; this is not true of other functions such as trigonometric function
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s, logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
s and exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
s.
Formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
are like polynomials, but allow infinitely many non-zero terms to occur, so that they do not have finite degree. Unlike polynomials they cannot in general be explicitly and fully written down (just like real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s cannot), but the rules for manipulating their terms are the same as for polynomials.
See also
- BinomialBinomialIn algebra, a binomial is a polynomial with two terms —the sum of two monomials—often bound by parenthesis or brackets when operated upon...
- List of polynomial topics
- Polynomials on vector spaces
- Power series