Adjugate matrix
Encyclopedia
In linear algebra
, the adjugate or classical adjoint of a square matrix is a matrix that plays a role similar to the inverse of a matrix; it can however be defined for any square matrix without the need to perform any divisions.
The adjugate has sometimes been called the "adjoint", but that terminology is ambiguous. Today, "adjoint" of a matrix normally refers to its corresponding adjoint operator
, which is its conjugate transpose
.
and A is an n×n matrix
with entries from R. The definition of the adjugate of A is a multi-step process:
The adjugate of A is the transpose
of the cofactor matrix of A:
.
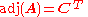That is, the adjugate of A is the n×n matrix whose (i,j) entry is the (j,i) cofactor of A:
.
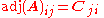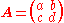
is
.
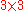matrix
.
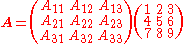Its adjugate is the transpose of the cofactor matrix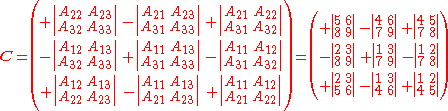
So that we have
where
.
Note that the adjugate is the transpose of the cofactor matrix. Thus, for instance, the (3,2) entry of the adjugate is the (2,3) cofactor of A.
.
The −6 in the third row, second column of the adjugate was computed as follows:
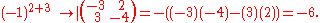
Again, the (3,2) entry of the adjugate is the (2,3) cofactor of A. Thus, the submatrix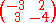
was obtained by deleting the second row and third column of the original matrix A.
for the determinant of an n×n matrix A, we have
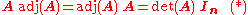
where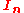
is the n×n identity matrix
. Indeed, the (i,i) entry of the product A adj(A) is the scalar product of row i of A with row i of the cofactor matrix C, which is simply the Laplace formula for det(A) expanded by row i. Moreover, for i ≠ j the (i,j) entry of the product is the scalar product of row i of A with row j of C, which is the Laplace formula for the determinant of a matrix whose i and j rows are equal and is therefore zero.
From this formula follows one of the most important results in matrix algebra: A matrix A over a commutative ring R is invertible if and only if det(A) is invertible in R.
For if A is an invertible matrix then
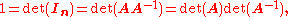
and if det(A) is a unit
then (*) above shows that
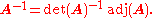
See also Cramer's rule
.
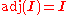
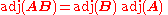
for all n×n matrices A and B.
The adjugate preserves transposition
:
.
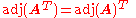Furthermore
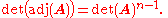
If p(t) = det(A − tI) is the characteristic polynomial
of A and we define the polynomial q(t) = (p(0) − p(t))/t, then
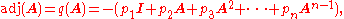
where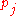
are the coefficients of p(t),
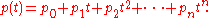
The adjugate also appears in the formula of the derivative
of the determinant
.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the adjugate or classical adjoint of a square matrix is a matrix that plays a role similar to the inverse of a matrix; it can however be defined for any square matrix without the need to perform any divisions.
The adjugate has sometimes been called the "adjoint", but that terminology is ambiguous. Today, "adjoint" of a matrix normally refers to its corresponding adjoint operator
Hermitian adjoint
In mathematics, specifically in functional analysis, each linear operator on a Hilbert space has a corresponding adjoint operator.Adjoints of operators generalize conjugate transposes of square matrices to infinite-dimensional situations...
, which is its conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
.
Definition
Suppose R is a commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
and A is an n×n matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with entries from R. The definition of the adjugate of A is a multi-step process:
- Define the (i,j) minorMinor (linear algebra)In linear algebra, a minor of a matrix A is the determinant of some smaller square matrix, cut down from A by removing one or more of its rows or columns...
of A, denoted Mij, as the determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the (n − 1)×(n − 1) matrix that results from deleting row i and column j of A. - Define the (i,j) cofactorCofactor (linear algebra)In linear algebra, the cofactor describes a particular construction that is useful for calculating both the determinant and inverse of square matrices...
of A as
-
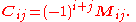
- Define the cofactor matrix of A, as the n×n matrix C whose (i,j) entry is the (i,j) cofactor of A.
The adjugate of A is the transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
of the cofactor matrix of A:
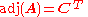.That is, the adjugate of A is the n×n matrix whose (i,j) entry is the (j,i) cofactor of A:
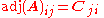.2 × 2 generic matrix
The adjugate of the 2 × 2 matrix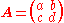is
.3 × 3 generic matrix
Consider the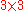 matrix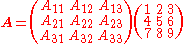.Its adjugate is the transpose of the cofactor matrix
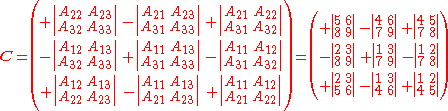
So that we have
where
.Note that the adjugate is the transpose of the cofactor matrix. Thus, for instance, the (3,2) entry of the adjugate is the (2,3) cofactor of A.
3 × 3 numeric matrix
As a specific example, we have.The −6 in the third row, second column of the adjugate was computed as follows:
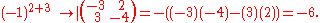
Again, the (3,2) entry of the adjugate is the (2,3) cofactor of A. Thus, the submatrix
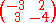
was obtained by deleting the second row and third column of the original matrix A.
Applications
As a consequence of Laplace's formulaLaplace expansion
In linear algebra, the Laplace expansion, named after Pierre-Simon Laplace, also called cofactor expansion, is an expression for the determinant |B| of...
for the determinant of an n×n matrix A, we have
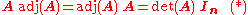
where
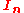is the n×n identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. Indeed, the (i,i) entry of the product A adj(A) is the scalar product of row i of A with row i of the cofactor matrix C, which is simply the Laplace formula for det(A) expanded by row i. Moreover, for i ≠ j the (i,j) entry of the product is the scalar product of row i of A with row j of C, which is the Laplace formula for the determinant of a matrix whose i and j rows are equal and is therefore zero.
From this formula follows one of the most important results in matrix algebra: A matrix A over a commutative ring R is invertible if and only if det(A) is invertible in R.
For if A is an invertible matrix then
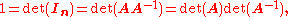
and if det(A) is a unit
Unit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
then (*) above shows that
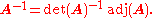
See also Cramer's rule
Cramer's rule
In linear algebra, Cramer's rule is a theorem, which gives an expression for the solution of a system of linear equations with as many equations as unknowns, valid in those cases where there is a unique solution...
.
Properties
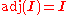
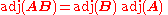
The adjugate has the propertiesfor all n×n matrices A and B.
The adjugate preserves transposition
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
:
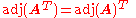.Furthermore
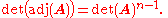
If p(t) = det(A − tI) is the characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of A and we define the polynomial q(t) = (p(0) − p(t))/t, then
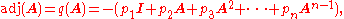
where
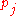are the coefficients of p(t),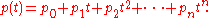The adjugate also appears in the formula of the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
.
External links
- Matrix Reference Manual
- Online matrix calculator (determinant, track, inverse, adjoint, transpose) Compute Adjugate matrix up to order 8