Zero matrix
Encyclopedia
In mathematics
, particularly linear algebra
, a zero matrix or null matrix is a matrix
with all its entries being zero
. Some examples of zero matrices are
The set of m×n matrices with entries in a ring
K forms a ring
. The zero matrix 
in 
is the matrix with all entries equal to 
, where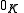 
is the additive identity
in K.
The zero matrix is the additive identity in
. That is, for all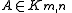 
it satisfies
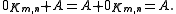
There is exactly one zero matrix of any given size m×n having entries in a given ring, so when the context is clear one often refers to the zero matrix. In general the zero element of a ring is unique and typically denoted as 0 without any subscript indicating the parent ring. Hence the examples above represent zero matrices over any ring.
The zero matrix represents the linear transformation
sending all vectors to the zero vector.
A matrix where just a single element is one and the rest are zero may be called a single-entry matrix.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a zero matrix or null matrix is a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with all its entries being zero
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
. Some examples of zero matrices are
The set of m×n matrices with entries in a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
K forms a ring
. The zero matrix in is the matrix with all entries equal to , where 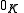is the additive identityAdditive identity
In mathematics the additive identity of a set which is equipped with the operation of addition is an element which, when added to any element x in the set, yields x...
in K.
The zero matrix is the additive identity in
. That is, for all 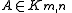it satisfies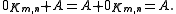There is exactly one zero matrix of any given size m×n having entries in a given ring, so when the context is clear one often refers to the zero matrix. In general the zero element of a ring is unique and typically denoted as 0 without any subscript indicating the parent ring. Hence the examples above represent zero matrices over any ring.
The zero matrix represents the linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
sending all vectors to the zero vector.
A matrix where just a single element is one and the rest are zero may be called a single-entry matrix.