
Minor (linear algebra)
Encyclopedia
In linear algebra
, a minor of a matrix
A is the determinant
of some smaller square matrix, cut down from A by removing one or more of its rows or columns. Minors obtained by removing just one row and one column from square matrices (first minors) are required for calculating matrix cofactor
s, which in turn are useful for computing both the determinant and inverse of square matrices.
Since there are:
ways to choose k rows from m rows, and there are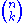
ways to choose k columns from n columns, there are a total of
minors of size k × k.
Mij is also called the minor of the element aij of matrix A.
A minor that is formed by removing only one row and column from a square matrix A (such as Mij) is called a first minor. When two rows and columns are removed, this is called a second minor.
Cij of a square matrix A is just (−1)i + j times the corresponding (n − 1) × (n − 1) minor Mij:
The cofactor matrix of A, or matrix of A cofactors, typically denoted C, is defined as the n×n matrix whose (i,j) entry is the (i,j) cofactor of A.
The transpose
of C is called the adjugate
or classical adjoint of A. (In modern terminology, the "adjoint" of a matrix most often refers to the corresponding adjoint operator.) Adjugate matrices are used to compute the inverse of square matrices.

suppose we wish to find the cofactor C23. The minor M23 is the determinant of the above matrix with row 2 and column 3 removed (the following is not standard notation):
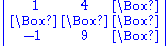 yields
yields 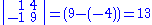
where the vertical bars around the matrix indicate that the determinant should be taken. Thus, C23 is (-1)2+3 M23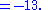
for the expansion of determinants. If all the cofactors of a square matrix A are collected to form a new matrix of the same size and then transposed, one obtains the adjugate of A, which is useful in calculating the inverse of small matrices.
Given an m × n matrix with real
entries (or entries from any other field
) and rank r, then there exists at least one non-zero r × r minor, while all larger minors are zero.
We will use the following notation for minors: if A is an m × n matrix, I is a subset
of {1,...,m} with k elements and J is a subset of {1,...,n} with k elements, then we write [A]I,J for the k × k minor of A that corresponds to the rows with index in I and the columns with index in J.
Both the formula for ordinary matrix multiplication
and the Cauchy-Binet formula
for the determinant of the product of two matrices are special cases of the following general statement about the minors of a product of two matrices.
Suppose that A is an m × n matrix, B is an n × p matrix, I is a subset
of {1,...,m} with k elements and J is a subset of {1,...,p} with k elements. Then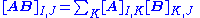
where the sum extends over all subsets K of {1,...,n} with k elements. This formula is a straightforward extension of the Cauchy-Binet formula.
, using the wedge product: the k-minors of a matrix are the entries in the kth exterior power map.
If the columns of a matrix are wedged together k at a time, the k × k minors appear as the components of the resulting k-vectors. For example, the 2 × 2 minors of the matrix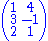
are −13 (from the first two rows), −7 (from the first and last row), and 5 (from the last two rows). Now consider the wedge product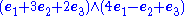
where the two expressions correspond to the two columns of our matrix. Using the properties of the wedge product, namely that it is bilinear
and
and
we can simplify this expression to
where the coefficients agree with the minors computed earlier.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a minor of a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
A is the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of some smaller square matrix, cut down from A by removing one or more of its rows or columns. Minors obtained by removing just one row and one column from square matrices (first minors) are required for calculating matrix cofactor
Cofactor (linear algebra)
In linear algebra, the cofactor describes a particular construction that is useful for calculating both the determinant and inverse of square matrices...
s, which in turn are useful for computing both the determinant and inverse of square matrices.
Detailed definition
Let A be an m × n matrix and k an integer with 0 < k ≤ m, and k ≤ n. A k × k minor of A is the determinant of a k × k matrix obtained from A by deleting m − k rows and n − k columns.Since there are:
 Binomial coefficientIn mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
Binomial coefficientIn mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
(read "m choose kBinomial coefficientIn mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
")
ways to choose k rows from m rows, and there are
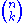
ways to choose k columns from n columns, there are a total of

minors of size k × k.
Nomenclature
The (i,j) minor (often denoted Mij) of an n × n square matrix A is defined as the determinant of the (n − 1) × (n − 1) matrix formed by removing from A its ith row and jth column. An (i,j) minor is also referred to as (i,j)th minor, or simply i,j minor.Mij is also called the minor of the element aij of matrix A.
A minor that is formed by removing only one row and column from a square matrix A (such as Mij) is called a first minor. When two rows and columns are removed, this is called a second minor.
Cofactors and adjugate or adjoint of a matrix
The (i,j) cofactorCofactor (linear algebra)
In linear algebra, the cofactor describes a particular construction that is useful for calculating both the determinant and inverse of square matrices...
Cij of a square matrix A is just (−1)i + j times the corresponding (n − 1) × (n − 1) minor Mij:
- Cij = (−1)i + j Mij
The cofactor matrix of A, or matrix of A cofactors, typically denoted C, is defined as the n×n matrix whose (i,j) entry is the (i,j) cofactor of A.
The transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
of C is called the adjugate
Adjugate matrix
In linear algebra, the adjugate or classical adjoint of a square matrix is a matrix that plays a role similar to the inverse of a matrix; it can however be defined for any square matrix without the need to perform any divisions....
or classical adjoint of A. (In modern terminology, the "adjoint" of a matrix most often refers to the corresponding adjoint operator.) Adjugate matrices are used to compute the inverse of square matrices.
Example
For example, given the matrix
suppose we wish to find the cofactor C23. The minor M23 is the determinant of the above matrix with row 2 and column 3 removed (the following is not standard notation):
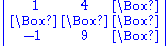 yields
yields 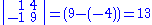
where the vertical bars around the matrix indicate that the determinant should be taken. Thus, C23 is (-1)2+3 M23
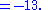
Complement
The complement, C, of a minor, M, of a square matrix, A, is formed by the determinant of the matrix A from which all the rows and columns associated with M have been removed. The complement of the first minor of an element aij is merely that element.Applications
The cofactors feature prominently in Laplace's formulaLaplace expansion
In linear algebra, the Laplace expansion, named after Pierre-Simon Laplace, also called cofactor expansion, is an expression for the determinant |B| of...
for the expansion of determinants. If all the cofactors of a square matrix A are collected to form a new matrix of the same size and then transposed, one obtains the adjugate of A, which is useful in calculating the inverse of small matrices.
Given an m × n matrix with real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
entries (or entries from any other field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
) and rank r, then there exists at least one non-zero r × r minor, while all larger minors are zero.
We will use the following notation for minors: if A is an m × n matrix, I is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of {1,...,m} with k elements and J is a subset of {1,...,n} with k elements, then we write [A]I,J for the k × k minor of A that corresponds to the rows with index in I and the columns with index in J.
- If I = J, then [A]I,J is called a principal minor.
- If the matrix that corresponds to a principal minor is a quadratic upper-left part of the larger matrix (i.e., it consists of matrix elements in rows and columns from 1 to k), then the principal minor is called a leading principal minor. For an n × n square matrix, there are n leading principal minors. (Not in agreement with a lot of books. Sometimes the leading principal minor is consider to be the leading k x k matrix.)
- For Hermitian matrices, the principal minors can be used to test for positive definitenessPositive-definite matrixIn linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
.
Both the formula for ordinary matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
and the Cauchy-Binet formula
Cauchy-Binet formula
In linear algebra, the Cauchy–Binet formula, named after Augustin-Louis Cauchy and Jacques Philippe Marie Binet, is an identity for the determinant of the product of two rectangular matrices of transpose shapes . It generalizes the statement that the determinant of a product of square matrices is...
for the determinant of the product of two matrices are special cases of the following general statement about the minors of a product of two matrices.
Suppose that A is an m × n matrix, B is an n × p matrix, I is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of {1,...,m} with k elements and J is a subset of {1,...,p} with k elements. Then
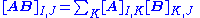
where the sum extends over all subsets K of {1,...,n} with k elements. This formula is a straightforward extension of the Cauchy-Binet formula.
Multilinear algebra approach
A more systematic, algebraic treatment of the minor concept is given in multilinear algebraMultilinear algebra
In mathematics, multilinear algebra extends the methods of linear algebra. Just as linear algebra is built on the concept of a vector and develops the theory of vector spaces, multilinear algebra builds on the concepts of p-vectors and multivectors with Grassmann algebra.-Origin:In a vector space...
, using the wedge product: the k-minors of a matrix are the entries in the kth exterior power map.
If the columns of a matrix are wedged together k at a time, the k × k minors appear as the components of the resulting k-vectors. For example, the 2 × 2 minors of the matrix
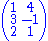
are −13 (from the first two rows), −7 (from the first and last row), and 5 (from the last two rows). Now consider the wedge product
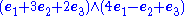
where the two expressions correspond to the two columns of our matrix. Using the properties of the wedge product, namely that it is bilinear
Bilinear
Bilinear may refer to:* Bilinear sampling, a method in computer graphics for choosing the color of a texture* Bilinear form* Bilinear interpolation* Bilinear map, a type of mathematical function between vector spaces...
and

and

we can simplify this expression to

where the coefficients agree with the minors computed earlier.

