Rotation matrix
Encyclopedia
In linear algebra
, a rotation matrix is a matrix
that is used to perform a rotation
in Euclidean space
. For example the matrix

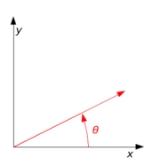
rotates points in the xy-Cartesian plane
counterclockwise through an angle θ about the origin of the Cartesian coordinate system
. To perform the rotation using a rotation matrix R, the position of each point must be represented by a column vector v, containing the coordinates of the point. A rotated vector is obtained by using the matrix multiplication
Rv. Since matrix multiplication has no effect on the zero vector (i.e., on the coordinates of the origin), rotation matrices can only be used to describe rotations about the origin of the coordinate system.
Rotation matrices provide a simple algebraic description of such rotations, and are used extensively for computations in geometry
, physics
, and computer graphics
. In 2-dimensional space, a rotation can be simply described by an angle θ of rotation
, but it can be also represented by the 4 entries of a rotation matrix with 2 rows and 2 columns. In 3-dimensional space, every rotation can be interpreted as a rotation by a given angle about a single fixed axis of rotation (see Euler's rotation theorem
), and hence it can be simply described by an angle and a vector with 3 entries. However, it can be also represented by the 9 entries of a rotation matrix with 3 rows and 3 columns. The notion of rotation is not commonly used in dimensions higher than 3; there is a notion of a rotational displacement, which can be represented by a matrix, but no associated single axis or angle.
Rotation matrices are square matrices, with real
entries. More specifically they can be characterized as orthogonal matrices
with determinant
1:
 .
.
The set of all such matrices of size n forms a group
, known as the special orthogonal group .
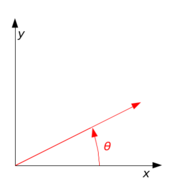 In two dimensions every rotation matrix has the following form:
In two dimensions every rotation matrix has the following form:
 .
.
This rotates column vectors by means of the following matrix multiplication
:
 .
.
So the coordinates (x',y') of the point (x,y) after rotation are:
 ,
, .
.
The direction of vector rotation is counterclockwise if θ is positive (e.g. 90°), and clockwise if θ is negative (e.g. -90°).
 .
.
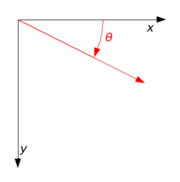 If a standard right-handed
If a standard right-handed
Cartesian coordinate system
is used, with the x axis to the right and the y axis up, the rotation R(θ) is counterclockwise. If a left-handed Cartesian coordinate system is used, with x directed to the right but y directed down, R(θ) is clockwise. Such non-standard orientations are rarely used in mathematics but are common in 2D computer graphics
, which often have the origin in the top left corner and the y-axis down the screen or page.
See below for other alternative conventions which may change the sense of the rotation produced by a rotation matrix.
 (90° counterclockwise rotation)
(90° counterclockwise rotation) (180° rotation in either direction – a half-turn)
(180° rotation in either direction – a half-turn) (270° counterclockwise rotation, the same as a 90° clockwise rotation)
(270° counterclockwise rotation, the same as a 90° clockwise rotation)
-like) rotation matrices rotate vectors about the x, y, or z axis, in three dimensions:

Each of these basic vector rotations typically appears counter-clockwise when the axis about which they occur points toward the observer, and the coordinate system is right-handed. Rz, for instance, would rotate toward the y-axis a vector aligned with the x-axis. This is similar to the rotation produced by the above mentioned 2-D rotation matrix. See below for alternative conventions which may apparently or actually invert the sense of the rotation produced by these matrices.
. For example, the product
represents a rotation whose yaw, pitch, and roll are α, β, and γ, respectively. Similarly, the product
represents a rotation whose Euler angles
are α, β, and γ (using the y-x-z convention for Euler angles).
The orthogonal matrix
(post-multiplying a column vector) corresponding to a clockwise/left-handed
rotation with Euler angles
 , with x-y-z convention, is given by:
, with x-y-z convention, is given by:

There are several methods to compute an axis and an angle from a rotation matrix (see also axis-angle). Here, we only describe the method based on the computation of the eigenvectors and eigenvalues of the rotation matrix. It is also possible to use the trace of the rotation matrix.
 Given a rotation matrix R, a vector u parallel to the rotation axis must satisfy
Given a rotation matrix R, a vector u parallel to the rotation axis must satisfy

since the rotation of around the rotation axis must result in
around the rotation axis must result in  . The equation above may be solved for
. The equation above may be solved for  which is unique up to a scalar factor.
which is unique up to a scalar factor.
Further, the equation may be rewritten

which shows that is the null space
is the null space
of . Viewed another way,
. Viewed another way,  is an eigenvector of R corresponding to the eigenvalue
is an eigenvector of R corresponding to the eigenvalue  (every rotation matrix must have this eigenvalue).
(every rotation matrix must have this eigenvalue).
 perpendicular to the axis. Then the angle of the rotation is the angle between
perpendicular to the axis. Then the angle of the rotation is the angle between  and
and  .
.
A much easier method, however, is to calculate the trace (i.e. the sum of the diagonal elements of the rotation matrix) which is .
.

This can be written more concisely as
where is the cross product matrix of u, ⊗ is the tensor product
is the cross product matrix of u, ⊗ is the tensor product
and I is the Identity matrix
. This is a matrix form of Rodrigues' rotation formula
, with
If the 3D space is right-handed, this rotation will be counterclockwise for an observer placed so that the axis u goes in his or her direction (Right-hand rule
).
 , where a is a rotation axis and θ a rotation angle,
, where a is a rotation axis and θ a rotation angle,
Some of these properties can be generalised to any number of dimensions. In other words, they hold for any rotation matrix .
.
For instance, in two dimensions the properties hold with the following exceptions:
, a rotation is an example of an isometry
, a transformation that moves points without changing the distances between them. Rotations are distinguished from other isometries by two additional properties: they leave (at least) one point fixed, and they leave "handedness" unchanged. By contrast, a translation
moves every point, a reflection exchanges left- and right-handed ordering, and a glide reflection
does both.
A rotation that does not leave "handedness" unchanged is an improper rotation
or a rotoinversion.
If we take the fixed point as the origin of a Cartesian coordinate system
, then every point can be given coordinates as a displacement from the origin. Thus we may work with the vector space
of displacements instead of the points themselves. Now suppose (p1,…,pn) are the coordinates of the vector p from the origin, O, to point P. Choose an orthonormal basis
for our coordinates; then the squared distance to P, by Pythagoras
, is
which we can compute using the matrix multiplication
A geometric rotation transforms lines to lines, and preserves ratios of distances between points. From these properties we can show that a rotation is a linear transformation
of the vectors, and thus can be written in matrix
form, Qp. The fact that a rotation preserves, not just ratios, but distances themselves, we can state as
or
Because this equation holds for all vectors, p, we conclude that every rotation matrix, Q, satisfies the orthogonality condition,
Rotations preserve handedness because they cannot change the ordering of the axes, which implies the special matrix condition,
Equally important, we can show that any matrix satisfying these two conditions acts as a rotation.

The product of two rotation matrices is a rotation matrix:
For n greater than 2, multiplication of n×n rotation matrices is not commutative.
Noting that any identity matrix
is a rotation matrix, and that matrix multiplication is associative, we may summarize all these properties by saying that the n×n rotation matrices form a group
, which for n > 2 is non-abelian
. Called a special orthogonal group, and denoted by SO(n), SO(n,R), SOn, or SOn(R), the group of n×n rotation matrices is isomorphic to the group of rotations in an n-dimensional space. This means that multiplication of rotation matrices corresponds to composition of rotations, applied in left-to-right order of their corresponding matrices.
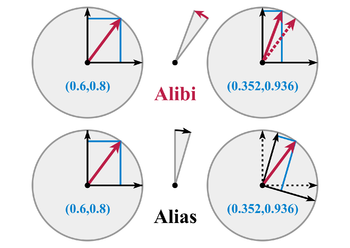 The interpretation of a rotation matrix can be subject to many ambiguities.
The interpretation of a rotation matrix can be subject to many ambiguities.
Alias or alibi transformation
Pre-multiplication or post-multiplication
Right- or left-handed coordinates
Vectors or forms
In most cases the effect of the ambiguity is equivalent to the effect of a transposition
of the rotation matrix.

If Q acts in a certain direction, v, purely as a scaling by a factor λ, then we have
so that
Thus λ is a root of the characteristic polynomial
for Q,
Two features are noteworthy. First, one of the roots (or eigenvalues) is 1, which tells us that some direction is unaffected by the matrix. For rotations in three dimensions, this is the axis of the rotation (a concept that has no meaning in any other dimension). Second, the other two roots are a pair of complex conjugates, whose product is 1 (the constant term of the quadratic), and whose sum is 2 cos θ (the negated linear term). This factorization is of interest for 3×3 rotation matrices because the same thing occurs for all of them. (As special cases, for a null rotation the "complex conjugates" are both 1, and for a 180° rotation they are both −1.) Furthermore, a similar factorization holds for any n×n rotation matrix. If the dimension, n, is odd, there will be a "dangling" eigenvalue of 1; and for any dimension the rest of the polynomial factors into quadratic terms like the one here (with the two special cases noted). We are guaranteed that the characteristic polynomial will have degree n and thus n eigenvalues. And since a rotation matrix commutes with its transpose, it is a normal matrix
, so can be diagonalized. We conclude that every rotation matrix, when expressed in a suitable coordinate system, partitions into independent rotations of two-dimensional subspaces, at most n⁄2 of them.
The sum of the entries on the main diagonal of a matrix is called the trace
; it does not change if we reorient the coordinate system, and always equals the sum of the eigenvalues. This has the convenient implication for 2×2 and 3×3 rotation matrices that the trace reveals the angle of rotation
, θ, in the two-dimensional (sub-)space. For a 2×2 matrix the trace is 2 cos(θ), and for a 3×3 matrix it is 1+2 cos(θ). In the three-dimensional case, the subspace consists of all vectors perpendicular to the rotation axis (the invariant direction, with eigenvalue 1). Thus we can extract from any 3×3 rotation matrix a rotation axis and an angle, and these completely determine the rotation.

with a2+b2 = 1. Therefore we may set a = cos θ and b = sin θ, for some angle θ. To solve for θ it is not enough to look at a alone or b alone; we must consider both together to place the angle in the correct quadrant, using a two-argument arctangent
function.
Now consider the first column of a 3×3 rotation matrix,
Although a2+b2 will probably not equal 1, but some value r2 < 1, we can use a slight variation of the previous computation to find a so-called Givens rotation that transforms the column to
zeroing b. This acts on the subspace spanned by the x and y axes. We can then repeat the process for the xz subspace to zero c. Acting on the full matrix, these two rotations produce the schematic form
Shifting attention to the second column, a Givens rotation of the yz subspace can now zero the z value. This brings the full matrix to the form
which is an identity matrix. Thus we have decomposed Q as
An n×n rotation matrix will have (n−1)+(n−2)+⋯+2+1, or
entries below the diagonal to zero. We can zero them by extending the same idea of stepping through the columns with a series of rotations in a fixed sequence of planes. We conclude that the set of n×n rotation matrices, each of which has n2 entries, can be parameterized by n(n−1)/2 angles.
In three dimensions this restates in matrix form an observation made by Euler
, so mathematicians call the ordered sequence of three angles Euler angles
. However, the situation is somewhat more complicated than we have so far indicated. Despite the small dimension, we actually have considerable freedom in the sequence of axis pairs we use; and we also have some freedom in the choice of angles. Thus we find many different conventions employed when three-dimensional rotations are parameterized for physics, or medicine, or chemistry, or other disciplines. When we include the option of world axes or body axes, 24 different sequences are possible. And while some disciplines call any sequence Euler angles, others give different names (Euler, Cardano, Tait-Bryan, Roll-pitch-yaw) to different sequences.
One reason for the large number of options is that, as noted previously, rotations in three dimensions (and higher) do not commute. If we reverse a given sequence of rotations, we get a different outcome. This also implies that we cannot compose two rotations by adding their corresponding angles. Thus Euler angles are not vectors
, despite a similarity in appearance as a triple of numbers.
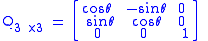
suggests a 2×2 rotation matrix,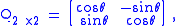
is embedded in the upper left corner: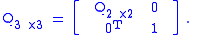
This is no illusion; not just one, but many, copies of n-dimensional rotations are found within (n+1)-dimensional rotations, as subgroup
s. Each embedding leaves one direction fixed, which in the case of 3×3 matrices is the rotation axis. For example, we have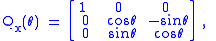
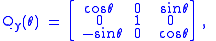
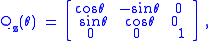
fixing the x axis, the y axis, and the z axis, respectively. The rotation axis need not be a coordinate axis; if u = (x,y,z) is a unit vector in the desired direction, then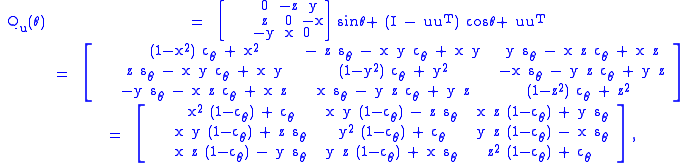
where cθ = cos θ, sθ = sin θ, is a rotation by angle θ leaving axis u fixed.
A direction in (n+1)-dimensional space will be a unit magnitude vector, which we may consider a point on a generalized sphere, Sn. Thus it is natural to describe the rotation group SO(n+1) as combining SO(n) and Sn. A suitable formalism is the fiber bundle
,
where for every direction in the "base space", Sn, the "fiber" over it in the "total space", SO(n+1), is a copy of the "fiber space", SO(n), namely the rotations that keep that direction fixed.
Thus we can build an n×n rotation matrix by starting with a 2×2 matrix, aiming its fixed axis on S2 (the ordinary sphere in three-dimensional space), aiming the resulting rotation on S3, and so on up through Sn−1. A point on Sn can be selected using n numbers, so we again have n(n−1)/2 numbers to describe any n×n rotation matrix.
In fact, we can view the sequential angle decomposition, discussed previously, as reversing this process. The composition of n−1 Givens rotations brings the first column (and row) to (1,0,…,0), so that the remainder of the matrix is a rotation matrix of dimension one less, embedded so as to leave (1,0,…,0) fixed.
, A. Thus AT = −A; and since the diagonal is necessarily zero, and since the upper triangle determines the lower one, A contains n(n−1)/2 independent numbers. Conveniently, I−A is invertible whenever A is skew-symmetric; thus we can recover the original matrix using the Cayley transform
,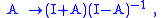
which maps any skew-symmetric matrix A to a rotation matrix. In fact, aside from the noted exceptions, we can produce any rotation matrix in this way. Although in practical applications we can hardly afford to ignore 180° rotations, the Cayley transform is still a potentially useful tool, giving a parameterization of most rotation matrices without trigonometric functions.
In three dimensions, for example, we have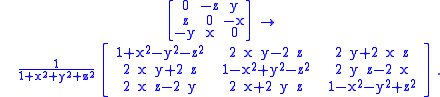
If we condense the skew entries into a vector, (x,y,z), then we produce a 90° rotation around the x axis for (1,0,0), around the y axis for (0,1,0), and around the z axis for (0,0,1). The 180° rotations are just out of reach; for, in the limit as x goes to infinity, (x,0,0) does approach a 180° rotation around the x axis, and similarly for other directions.
, the special orthogonal group, SO(n). This algebraic structure
is coupled with a topological structure, in that the operations of multiplication and taking the inverse (which here is merely transposition) are continuous functions of the matrix entries. Thus SO(n) is a classic example of a topological group
. (In purely topological terms, it is a compact manifold.) Furthermore, the operations are not only continuous, but smooth
, so SO(n) is a differentiable manifold
and a Lie group
.
Most properties of rotation matrices depend very little on the dimension, n; yet in Lie group theory we see systematic differences between even dimensions and odd dimensions. As well, there are some irregularities below n = 5; for example, SO(4) is, anomalously, not a simple Lie group
, but instead isomorphic to the product
of S3 and SO(3).
, a linear space equipped with a bilinear alternating product is called a bracket. The algebra for SO(n) is denoted by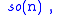
and consists of all skew-symmetric
n×n matrices (as implied by differentiating the orthogonality condition
, I = QTQ). The bracket, [A1,A2], of two skew-symmetric matrices is defined to be A1A2−A2A1, which is again a skew-symmetric matrix. This Lie algebra bracket captures the essence of the Lie group product via infinitesimals.
For 2×2 rotation matrices, the Lie algebra is a one-dimensional vector space, multiples of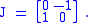
Here the bracket always vanishes, which tells us that, in two dimensions, rotations commute. Not so in any higher dimension. For 3×3 rotation matrices, we have a three-dimensional vector space with the convenient basis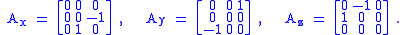
The Lie brackets of these generators are as follows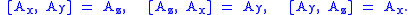
We can conveniently identify any matrix in this Lie algebra with a vector in R3,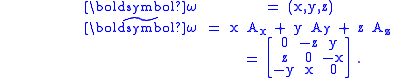
Under this identification, the so(3) bracket has a memorable description; it is the vector cross product
,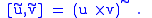
The matrix identified with a vector v is also memorable, because
Notice this implies that v is in the null space
of the skew-symmetric matrix with which it is identified, because v×v is always the zero vector.
, which we define using the familiar power series for ex ,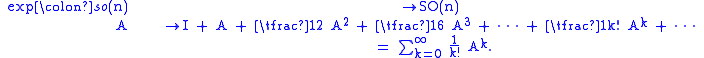
For any skew-symmetric A, exp(A) is always a rotation matrix.
An important practical example is the 3×3 case, where we have seen we can identify every skew-symmetric matrix with a vector ω = uθ, where u = (x,y,z) is a unit magnitude vector. Recall that u is in the null space of the matrix associated with ω, so that if we use a basis with u as the z axis the final column and row will be zero. Thus we know in advance that the exponential matrix must leave u fixed. It is mathematically impossible to supply a straightforward formula for such a basis as a function of u (its existence would violate the hairy ball theorem
), but direct exponentiation is possible, and yields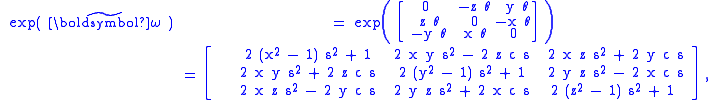
where c = cos θ⁄2, s = sin θ⁄2. We recognize this as our matrix for a rotation around axis u by angle θ. We also note that this mapping of skew-symmetric matrices is quite different from the Cayley transform discussed earlier.
In any dimension, if we choose some nonzero A and consider all its scalar multiples, exponentiation yields rotation matrices along a geodesic
of the group manifold, forming a one-parameter subgroup of the Lie group. More broadly, the exponential map provides a homeomorphism
between a neighborhood of the origin in the Lie algebra and a neighborhood of the identity in the Lie group. In fact, we can produce any rotation matrix as the exponential of some skew-symmetric matrix, so for these groups the exponential map is a surjection.
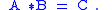
When exp(A) and exp(B) commute (which always happens for 2×2 matrices, but not higher), then C = A+B, mimicking the behavior of complex exponentiation. The general case is given by the BCH formula, a series expanded in terms of the bracket . For matrices, the bracket is the same operation as the commutator
, which detects lack of commutativity in multiplication. The general formula begins as follows.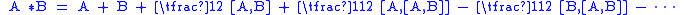
Representation of a rotation matrix as a sequential angle decomposition, as in Euler angles, may tempt us to treat rotations as a vector space, but the higher order terms in the BCH formula reveal that to be a mistake.
We again take special interest in the 3×3 case, where [A,B] equals the cross product, A×B. If A and B are linearly independent, then A, B, and A×B can be used as a basis; if not, then A and B commute. And conveniently, in this dimension the summation in the BCH formula has a closed form as αA+βB+γ(A×B).
and path-connected
manifold
, and thus locally compact
and connected
. However, it is not simply connected
, so Lie theory tells us it is a kind of "shadow" (a homomorphic image) of a universal covering group
. Often the covering group, which in this case is the spin group denoted by Spin(n), is simpler and more natural to work with .
In the case of planar rotations, SO(2) is topologically a circle
, S1. Its universal covering group, Spin(2), is isomorphic to the real line
, R, under addition. In other words, whenever we use angles of arbitrary magnitude, which we often do, we are essentially taking advantage of the convenience of the "mother space". Every 2×2 rotation matrix is produced by a countable infinity of angles, separated by integer multiples of 2π. Correspondingly, the fundamental group
of SO(2) is isomorphic to the integers, Z.
In the case of spatial rotations, SO(3) is topologically equivalent to three-dimensional real projective space
, RP3. Its universal covering group, Spin(3), is isomorphic to the 3-sphere, S3. Every 3×3 rotation matrix is produced by two opposite points on the sphere. Correspondingly, the fundamental group
of SO(3) is isomorphic to the two-element group, Z2. We can also describe Spin(3) as isomorphic to quaternion
s of unit norm under multiplication, or to certain 4×4 real matrices, or to 2×2 complex special unitary matrices
.
Concretely, a unit quaternion, q, with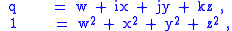
produces the rotation matrix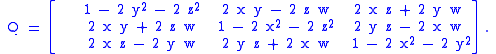
This is our third version of this matrix, here as a rotation around non-unit axis vector (x,y,z) by angle 2θ, where cos θ = w and |sin θ| = ||(x,y,z)||. (The proper sign for sin θ is implied once the signs of the axis components are decided.)
Many features of this case are the same for higher dimensions. The coverings are all two-to-one, with SO(n), n > 2, having fundamental group Z2. The natural setting for these groups is within a Clifford algebra
. And the action of the rotations is produced by a kind of "sandwich", denoted by qvq∗.
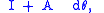
where dθ is vanishingly small. These matrices do not satisfy all the same properties as ordinary finite rotation matrices under the usual treatment of infinitesimals . To understand what this means, consider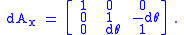
We first test the orthogonality condition, QTQ = I. The product is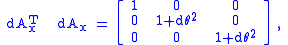
differing from an identity matrix by second order infinitesimals, which we discard. So to first order, an infinitesimal rotation matrix is an orthogonal matrix. Next we examine the square of the matrix.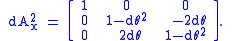
Again discarding second order effects, we see that the angle simply doubles. This hints at the most essential difference in behavior, which we can exhibit with the assistance of a second infinitesimal rotation,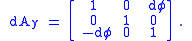
Compare the products dAxdAy and dAydAx.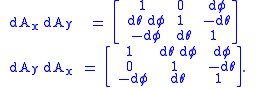
Since dθ dφ is second order, we discard it; thus, to first order, multiplication of infinitesimal rotation matrices is commutative. In fact,
again to first order. Put in other words, the order in which infinitesimal rotations are applied is irrelevant, this useful fact makes, for example, derivation of rigid body rotation relatively simple.
But we must always be careful to distinguish (the first order treatment of) these infinitesimal rotation matrices from both finite rotation matrices and from derivatives of rotation matrices (namely skew-symmetric matrices). Contrast the behavior of finite rotation matrices in the BCH formula with that of infinitesimal rotation matrices, where all the commutator terms will be second order infinitesimals so we do have a vector space.
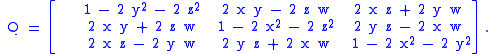
Now every quaternion
component appears multiplied by two in a term of degree two, and if all such terms are zero what's left is an identity matrix. This leads to an efficient, robust conversion from any quaternion — whether unit, nonunit, or even zero — to a 3×3 rotation matrix.
Nq = w^2 + x^2 + y^2 + z^2
if Nq > 0.0 then s = 2/Nq else s = 0.0
X = x*s; Y = y*s; Z = z*s
wX = w*X; wY = w*Y; wZ = w*Z
xX = x*X; xY = x*Y; xZ = x*Z
yY = y*Y; yZ = y*Z; zZ = z*Z
[ 1.0-(yY+zZ) xY-wZ xZ+wY ]
[ xY+wZ 1.0-(xX+zZ) yZ-wX ]
[ xZ-wY yZ+wX 1.0-(xX+yY) ]
Freed from the demand for a unit quaternion, we find that nonzero quaternions act as homogeneous coordinates
for 3×3 rotation matrices. The Cayley transform, discussed earlier, is obtained by scaling the quaternion so that its w component is 1. For a 180° rotation around any axis, w will be zero, which explains the Cayley limitation.
The sum of the entries along the main diagonal (the trace
), plus one, equals 4−4(x2+y2+z2), which is 4w2. Thus we can write the trace itself as 2w2+2w2−1; and from the previous version of the matrix we see that the diagonal entries themselves have the same form: 2x2+2w2−1, 2y2+2w2−1, and 2z2+2w2−1. So we can easily compare the magnitudes of all four quaternion components using the matrix diagonal. We can, in fact, obtain all four magnitudes using sums and square roots, and choose consistent signs using the skew-symmetric part of the off-diagonal entries.
t = Qxx+Qyy+Qzz (trace of Q)
r = sqrt(1+t)
w = 0.5*r
x = copysign(0.5*sqrt(1+Qxx-Qyy-Qzz), Qzy-Qyz)
y = copysign(0.5*sqrt(1-Qxx+Qyy-Qzz), Qxz-Qzx)
z = copysign(0.5*sqrt(1-Qxx-Qyy+Qzz), Qyx-Qxy)
where copysign(x,y) is x with the sign of y: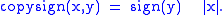
Alternatively, use a single square root and division
t = Qxx+Qyy+Qzz
r = sqrt(1+t)
s = 0.5/r
w = 0.5*r
x = (Qzy-Qyz)*s
y = (Qxz-Qzx)*s
z = (Qyx-Qxy)*s
This is numerically stable so long as the trace, t, is not negative; otherwise, we risk dividing by (nearly) zero. In that case, suppose Qxx is the largest diagonal entry, so x will have the largest magnitude (the other cases are similar); then the following is safe.
t = Qxx+Qyy+Qzz
r = sqrt(1+t)
s = 0.5/r
w = (Qzy-Qyz)*s
x = 0.5*r
y = (Qxy+Qyx)*s
z = (Qzx+Qxz)*s
If the matrix contains significant error, such as accumulated numerical error, we may construct a symmetric 4×4 matrix,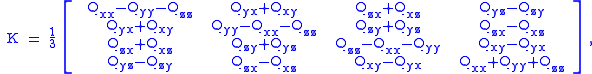
and find the eigenvector, (w,x,y,z), of its largest magnitude eigenvalue. (If Q is truly a rotation matrix, that value will be 1.) The quaternion so obtained will correspond to the rotation matrix closest to the given matrix .
can adjust them to be an orthonormal basis. Stated in terms of numerical linear algebra
, we convert M to an orthogonal matrix, Q, using QR decomposition
. However, we often prefer a Q "closest" to M, which this method does not accomplish. For that, the tool we want is the polar decomposition .
To measure closeness, we may use any matrix norm invariant under orthogonal transformations. A convenient choice is the Frobenius norm, ||Q−M||F, squared, which is the sum of the squares of the element differences. Writing this in terms of the trace
, Tr, our goal is,
Though written in matrix terms, the objective function is just a quadratic polynomial. We can minimize it in the usual way, by finding where its derivative is zero. For a 3×3 matrix, the orthogonality constraint implies six scalar equalities that the entries of Q must satisfy. To incorporate the constraint(s), we may employ a standard technique, Lagrange multipliers
, assembled as a symmetric matrix, Y. Thus our method is:
In general, we obtain the equation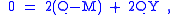
so that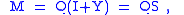
where Q is orthogonal and S is symmetric. To ensure a minimum, the Y matrix (and hence S) must be positive definite. Linear algebra calls QS the polar decomposition of M, with S the positive square root of S2 = MTM.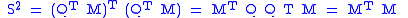
When M is non-singular, the Q and S factors of the polar decomposition are uniquely determined. However, the determinant of S is positive because S is positive definite, so Q inherits the sign of the determinant of M. That is, Q is only guaranteed to be orthogonal, not a rotation matrix. This is unavoidable; an M with negative determinant has no uniquely-defined closest rotation matrix.
c = cos(θ); s = sin(θ); C = 1-c
then Q is
[ xxC+c xyC-zs xzC+ys ]
[ yxC+zs yyC+c yzC-xs ]
[ zxC-ys zyC+xs zzC+c ]
Determining an axis and angle, like determining a quaternion, is only possible up to sign; that is, (u,θ) and (−u,−θ) correspond to the same rotation matrix, just like q and −q. As well, axis-angle extraction presents additional difficulties. The angle can be restricted to be from 0° to 180°, but angles are formally ambiguous by multiples of 360°. When the angle is zero, the axis is undefined. When the angle is 180°, the matrix becomes symmetric, which has implications in extracting the axis. Near multiples of 180°, care is needed to avoid numerical problems: in extracting the angle, a two-argument arctangent
with atan2
(sin θ,cos θ) equal to θ avoids the insensitivity of arccosine; and in computing the axis magnitude to force unit magnitude, a brute-force approach can lose accuracy through underflow .
A partial approach is as follows.
x = Qzy-Qyz
y = Qxz-Qzx
z = Qyx-Qxy
r = sqrt(x2 + y2 + z2)
t = Qxx+Qyy+Qzz (trace of matrix Q)
θ = atan2(r,t−1)
The x, y, and z components of the axis would then be divided by r. A fully robust approach will use different code when the trace t is negative, as with quaternion extraction. When r is zero because the angle is zero, an axis must be provided from some source other than the matrix.
(used here in the broad sense). The first difficulty is to establish which of the twenty-four variations of Cartesian axis order we will use. Suppose the three angles are θ1, θ2, θ3; physics and chemistry may interpret these as
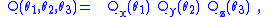
while aircraft dynamics may use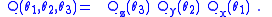
One systematic approach begins with choosing the right-most axis. Among all permutation
s of (x,y,z), only two place that axis first; one is an even permutation and the other odd. Choosing parity thus establishes the middle axis. That leaves two choices for the left-most axis, either duplicating the first or not. These three choices gives us 3×2×2 = 12 variations; we double that to 24 by choosing static or rotating axes.
This is enough to construct a matrix from angles, but triples differing in many ways can give the same rotation matrix. For example, suppose we use the zyz convention above; then we have the following equivalent pairs:
Angles for any order can be found using a concise common routine .
The problem of singular alignment, the mathematical analog of physical gimbal lock
, occurs when the middle rotation aligns the axes of the first and last rotations. It afflicts every axis order at either even or odd multiples of 90°. These singularities are not characteristic of the rotation matrix as such, and only occur with the usage of Euler angles.
The singularities are avoided when considering and manipulating the rotation matrix as orthonormal row vectors (in 3D applications often named 'right'-vector, 'up'-vector and 'out'-vector) instead of as angles. The singularities are also avoided when working with quaternions.
Since SO(n) is a connected and locally compact Lie group, we have a simple standard criterion for uniformity, namely that the distribution be unchanged when composed with any arbitrary rotation (a Lie group "translation"). This definition corresponds to what is called Haar measure
. show how to use the Cayley transform to generate and test matrices according to this criterion.
We can also generate a uniform distribution in any dimension using the subgroup algorithm of . This recursively exploits the nested dimensions group structure of SO(n), as follows. Generate a uniform angle and construct a 2×2 rotation matrix. To step from n to n+1, generate a vector v uniformly distributed on the n-sphere, Sn, embed the n×n matrix in the next larger size with last column (0,…,0,1), and rotate the larger matrix so the last column becomes v.
As usual, we have special alternatives for the 3×3 case. Each of these methods begins with three independent random scalars uniformly distributed on the unit interval. takes advantage of the odd dimension to change a Householder reflection to a rotation by negation, and uses that to aim the axis of a uniform planar rotation.
Another method uses unit quaternions. Multiplication of rotation matrices is homomorphic to multiplication of quaternions, and multiplication by a unit quaternion rotates the unit sphere. Since the homomorphism is a local isometry
, we immediately conclude that to produce a uniform distribution on SO(3) we may use a uniform distribution on S3.
Euler angles can also be used, though not with each angle uniformly distributed .
For the axis-angle form, the axis is uniformly distributed over the unit sphere of directions, S2, while the angle has the non-uniform distribution over [0,π] noted previously .
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a rotation matrix is a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
that is used to perform a rotation
Rotation (mathematics)
In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. For example the matrix

rotates points in the xy-Cartesian plane
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
counterclockwise through an angle θ about the origin of the Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
. To perform the rotation using a rotation matrix R, the position of each point must be represented by a column vector v, containing the coordinates of the point. A rotated vector is obtained by using the matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
Rv. Since matrix multiplication has no effect on the zero vector (i.e., on the coordinates of the origin), rotation matrices can only be used to describe rotations about the origin of the coordinate system.
Rotation matrices provide a simple algebraic description of such rotations, and are used extensively for computations in geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, and computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
. In 2-dimensional space, a rotation can be simply described by an angle θ of rotation
Angle of rotation
In mathematics, the angle of rotation is a measurement of the amount, the angle, that a figure is rotated about a fixed point, often the center of a circle....
, but it can be also represented by the 4 entries of a rotation matrix with 2 rows and 2 columns. In 3-dimensional space, every rotation can be interpreted as a rotation by a given angle about a single fixed axis of rotation (see Euler's rotation theorem
Euler's rotation theorem
In geometry, Euler's rotation theorem states that, in three-dimensional space, any displacement of a rigid body such that a point on the rigid body remains fixed, is equivalent to a single rotation about some axis that runs through the fixed point. It also means that the composition of two...
), and hence it can be simply described by an angle and a vector with 3 entries. However, it can be also represented by the 9 entries of a rotation matrix with 3 rows and 3 columns. The notion of rotation is not commonly used in dimensions higher than 3; there is a notion of a rotational displacement, which can be represented by a matrix, but no associated single axis or angle.
Rotation matrices are square matrices, with real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
entries. More specifically they can be characterized as orthogonal matrices
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
with determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
1:
 .
.The set of all such matrices of size n forms a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, known as the special orthogonal group .
Rotations in two dimensions

 .
.This rotates column vectors by means of the following matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
:
 .
.So the coordinates (x',y') of the point (x,y) after rotation are:
 ,
, .
.The direction of vector rotation is counterclockwise if θ is positive (e.g. 90°), and clockwise if θ is negative (e.g. -90°).
 .
.Non-standard orientation of the coordinate system

Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
is used, with the x axis to the right and the y axis up, the rotation R(θ) is counterclockwise. If a left-handed Cartesian coordinate system is used, with x directed to the right but y directed down, R(θ) is clockwise. Such non-standard orientations are rarely used in mathematics but are common in 2D computer graphics
2D computer graphics
2D computer graphics is the computer-based generation of digital images—mostly from two-dimensional models and by techniques specific to them...
, which often have the origin in the top left corner and the y-axis down the screen or page.
See below for other alternative conventions which may change the sense of the rotation produced by a rotation matrix.
Common rotations
Particularly useful are the matrices for 90° and 180° rotations: (90° counterclockwise rotation)
(90° counterclockwise rotation) (180° rotation in either direction – a half-turn)
(180° rotation in either direction – a half-turn) (270° counterclockwise rotation, the same as a 90° clockwise rotation)
(270° counterclockwise rotation, the same as a 90° clockwise rotation)Basic rotations
The following three basic (gimbalGimbal
A gimbal is a pivoted support that allows the rotation of an object about a single axis. A set of two gimbals, one mounted on the other with pivot axes orthogonal, may be used to allow an object mounted on the innermost gimbal to remain immobile regardless of the motion of its support...
-like) rotation matrices rotate vectors about the x, y, or z axis, in three dimensions:

Each of these basic vector rotations typically appears counter-clockwise when the axis about which they occur points toward the observer, and the coordinate system is right-handed. Rz, for instance, would rotate toward the y-axis a vector aligned with the x-axis. This is similar to the rotation produced by the above mentioned 2-D rotation matrix. See below for alternative conventions which may apparently or actually invert the sense of the rotation produced by these matrices.
General rotations
Other rotation matrices can be obtained from these three using matrix multiplicationMatrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
. For example, the product

represents a rotation whose yaw, pitch, and roll are α, β, and γ, respectively. Similarly, the product

represents a rotation whose Euler angles
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
are α, β, and γ (using the y-x-z convention for Euler angles).
The orthogonal matrix
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
(post-multiplying a column vector) corresponding to a clockwise/left-handed
Right-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
rotation with Euler angles
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
 , with x-y-z convention, is given by:
, with x-y-z convention, is given by:
Conversion from and to axis-angle
Every rotation in three dimensions is defined by its axis — a direction that is left fixed by the rotation — and its angle — the amount of rotation about that axis (Euler rotation theorem).There are several methods to compute an axis and an angle from a rotation matrix (see also axis-angle). Here, we only describe the method based on the computation of the eigenvectors and eigenvalues of the rotation matrix. It is also possible to use the trace of the rotation matrix.
Determining the axis


since the rotation of
 around the rotation axis must result in
around the rotation axis must result in  . The equation above may be solved for
. The equation above may be solved for  which is unique up to a scalar factor.
which is unique up to a scalar factor.Further, the equation may be rewritten

which shows that
 is the null space
is the null spaceNull space
In linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...
of
 . Viewed another way,
. Viewed another way,  is an eigenvector of R corresponding to the eigenvalue
is an eigenvector of R corresponding to the eigenvalue  (every rotation matrix must have this eigenvalue).
(every rotation matrix must have this eigenvalue).Determining the angle
To find the angle of a rotation, once the axis of the rotation is known, select a vector perpendicular to the axis. Then the angle of the rotation is the angle between
perpendicular to the axis. Then the angle of the rotation is the angle between  and
and  .
.A much easier method, however, is to calculate the trace (i.e. the sum of the diagonal elements of the rotation matrix) which is
 .
.Rotation matrix from axis and angle
For some applications, it is helpful to be able to make a rotation with a given axis. Given a unit vector u = (ux, uy, uz), where ux2 + uy2 + uz2 = 1, the matrix for a rotation by an angle of θ about an axis in the direction of u is
This can be written more concisely as

where
 is the cross product matrix of u, ⊗ is the tensor product
is the cross product matrix of u, ⊗ is the tensor productTensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
and I is the Identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. This is a matrix form of Rodrigues' rotation formula
Rodrigues' rotation formula
In the theory of three-dimensional rotation, Rodrigues' rotation formula is an efficient algorithm for rotating a vector in space, given an axis and angle of rotation. By extension, this can be used to transform all three basis vectors to compute a rotation matrix from an axis-angle representation...
, with

If the 3D space is right-handed, this rotation will be counterclockwise for an observer placed so that the axis u goes in his or her direction (Right-hand rule
Right-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
).
Properties of a rotation matrix
In three dimensions, for any rotation matrix , where a is a rotation axis and θ a rotation angle,
, where a is a rotation axis and θ a rotation angle,-
 (i.e.,
(i.e.,  is an orthogonal matrixOrthogonal matrixIn linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
is an orthogonal matrixOrthogonal matrixIn linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
) -
 (i.e, the determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
(i.e, the determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of is 1)
is 1) -

-
 (where
(where  is the identity matrixIdentity matrixIn linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
is the identity matrixIdentity matrixIn linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
) - The eigenvalues of
 are
are
-
-
- where i is the standard imaginary unitImaginary unitIn mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
with the property
- The traceTrace (linear algebra)In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of is
is  equivalent to the sum of its eigenvalues.
equivalent to the sum of its eigenvalues.
- The trace
-
Some of these properties can be generalised to any number of dimensions. In other words, they hold for any rotation matrix
 .
.For instance, in two dimensions the properties hold with the following exceptions:
- a is not a given axis, but a point (rotation center) which must coincide with the origin of the coordinate system in which the rotation is represented.
- Consequently, the four elements of the rotation matrix depend only on θ, hence we write
 , rather than
, rather than 
- The eigenvalues of
 are
are 
- The traceTrace (linear algebra)In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of is
is  equivalent to the sum of its eigenvalues.
equivalent to the sum of its eigenvalues.
Examples
- The 2×2 rotation matrix

corresponds to a 90° planar rotation. - The transpose of the 2×2 matrix

is its inverse, but since its determinant is −1 this is not a rotation matrix; it is a reflection across the line 11y = 2x.
- The 3×3 rotation matrix
x axis in three-dimensional space.
corresponds to a −30° rotation around the - The 3×3 rotation matrix
- The 3×3 rotation matrix

corresponds to a rotation of approximately -74° around the axis (−1⁄3,2⁄3,2⁄3) in three-dimensional space. - The 3×3 permutation matrixPermutation matrixIn mathematics, in matrix theory, a permutation matrix is a square binary matrix that has exactly one entry 1 in each row and each column and 0s elsewhere...

is a rotation matrix, as is the matrix of any even permutation, and rotates through 120° about the axis x = y = z.
- The 3×3 matrix

has determinant +1, but its transpose is not its inverse, so it is not a rotation matrix. - The 4×3 matrix

is not square, and so cannot be a rotation matrix; yet MTM yields a 3×3 identity matrix (the columns are orthonormal). - The 4×4 matrix

describes an isoclinic rotation, a rotation through equal angles (180°) through two orthogonal planes.
- The 5×5 rotation matrix

rotates vectors in the plane of the first two coordinate axes 90°, rotates vectors in the plane of the next two axes 180°, and leaves the last coordinate axis unmoved.
Geometry
In Euclidean geometryEuclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, a rotation is an example of an isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
, a transformation that moves points without changing the distances between them. Rotations are distinguished from other isometries by two additional properties: they leave (at least) one point fixed, and they leave "handedness" unchanged. By contrast, a translation
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
moves every point, a reflection exchanges left- and right-handed ordering, and a glide reflection
Glide reflection
In geometry, a glide reflection is a type of isometry of the Euclidean plane: the combination of a reflection in a line and a translation along that line. Reversing the order of combining gives the same result...
does both.
A rotation that does not leave "handedness" unchanged is an improper rotation
Improper rotation
In 3D geometry, an improper rotation, also called rotoreflection or rotary reflection is, depending on context, a linear transformation or affine transformation which is the combination of a rotation about an axis and a reflection in a plane perpendicular to the axis.Equivalently it is the...
or a rotoinversion.
If we take the fixed point as the origin of a Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
, then every point can be given coordinates as a displacement from the origin. Thus we may work with the vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of displacements instead of the points themselves. Now suppose (p1,…,pn) are the coordinates of the vector p from the origin, O, to point P. Choose an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
for our coordinates; then the squared distance to P, by Pythagoras
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
, is
which we can compute using the matrix multiplication

A geometric rotation transforms lines to lines, and preserves ratios of distances between points. From these properties we can show that a rotation is a linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
of the vectors, and thus can be written in matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
form, Qp. The fact that a rotation preserves, not just ratios, but distances themselves, we can state as

or

Because this equation holds for all vectors, p, we conclude that every rotation matrix, Q, satisfies the orthogonality condition,

Rotations preserve handedness because they cannot change the ordering of the axes, which implies the special matrix condition,

Equally important, we can show that any matrix satisfying these two conditions acts as a rotation.
Multiplication
The inverse of a rotation matrix is its transpose, which is also a rotation matrix:
The product of two rotation matrices is a rotation matrix:

For n greater than 2, multiplication of n×n rotation matrices is not commutative.

Noting that any identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
is a rotation matrix, and that matrix multiplication is associative, we may summarize all these properties by saying that the n×n rotation matrices form a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, which for n > 2 is non-abelian
Nonabelian group
In mathematics, a non-abelian group, also sometimes called a non-commutative group, is a group in which there are at least two elements a and b of G such that a * b ≠ b * a...
. Called a special orthogonal group, and denoted by SO(n), SO(n,R), SOn, or SOn(R), the group of n×n rotation matrices is isomorphic to the group of rotations in an n-dimensional space. This means that multiplication of rotation matrices corresponds to composition of rotations, applied in left-to-right order of their corresponding matrices.
Ambiguities

Alias or alibi transformation
- The change in a vector's coordinates can be due to a turn of the coordinate system (alias) or a turn of the vector (alibi). Any rotation can be legitimately described both ways, as vectors and coordinate systems actually rotate with respect to each other. Throughout this article, we chose the alibi approach to describe rotations.
Pre-multiplication or post-multiplication
- The vector can be pre-multiplied by a rotation matrix (Rv, where v is a column vector), or post-multiplied by it (vR, where v is a row vector). Throughout this article, we described rotations produced by means of a pre-multiplication.
Right- or left-handed coordinates
- The matrix and the vector can be represented with respect to a right-handed or left-handed coordinate system. Throughout the article, we assumed a right-handed orientation, unless otherwise specified.
Vectors or forms
- The vector space has a dual spaceDual spaceIn mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of linear forms, and the matrix can act on either vectors or forms.
In most cases the effect of the ambiguity is equivalent to the effect of a transposition
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
of the rotation matrix.
Independent planes
Consider the 3×3 rotation matrix
If Q acts in a certain direction, v, purely as a scaling by a factor λ, then we have

so that

Thus λ is a root of the characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
for Q,

Two features are noteworthy. First, one of the roots (or eigenvalues) is 1, which tells us that some direction is unaffected by the matrix. For rotations in three dimensions, this is the axis of the rotation (a concept that has no meaning in any other dimension). Second, the other two roots are a pair of complex conjugates, whose product is 1 (the constant term of the quadratic), and whose sum is 2 cos θ (the negated linear term). This factorization is of interest for 3×3 rotation matrices because the same thing occurs for all of them. (As special cases, for a null rotation the "complex conjugates" are both 1, and for a 180° rotation they are both −1.) Furthermore, a similar factorization holds for any n×n rotation matrix. If the dimension, n, is odd, there will be a "dangling" eigenvalue of 1; and for any dimension the rest of the polynomial factors into quadratic terms like the one here (with the two special cases noted). We are guaranteed that the characteristic polynomial will have degree n and thus n eigenvalues. And since a rotation matrix commutes with its transpose, it is a normal matrix
Normal matrix
A complex square matrix A is a normal matrix ifA^*A=AA^* \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT...
, so can be diagonalized. We conclude that every rotation matrix, when expressed in a suitable coordinate system, partitions into independent rotations of two-dimensional subspaces, at most n⁄2 of them.
The sum of the entries on the main diagonal of a matrix is called the trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
; it does not change if we reorient the coordinate system, and always equals the sum of the eigenvalues. This has the convenient implication for 2×2 and 3×3 rotation matrices that the trace reveals the angle of rotation
Angle of rotation
In mathematics, the angle of rotation is a measurement of the amount, the angle, that a figure is rotated about a fixed point, often the center of a circle....
, θ, in the two-dimensional (sub-)space. For a 2×2 matrix the trace is 2 cos(θ), and for a 3×3 matrix it is 1+2 cos(θ). In the three-dimensional case, the subspace consists of all vectors perpendicular to the rotation axis (the invariant direction, with eigenvalue 1). Thus we can extract from any 3×3 rotation matrix a rotation axis and an angle, and these completely determine the rotation.
Sequential angles
The constraints on a 2×2 rotation matrix imply that it must have the form
with a2+b2 = 1. Therefore we may set a = cos θ and b = sin θ, for some angle θ. To solve for θ it is not enough to look at a alone or b alone; we must consider both together to place the angle in the correct quadrant, using a two-argument arctangent
Atan2
In trigonometry, the two-argument function atan2 is a variation of the arctangent function. For any real arguments and not both equal to zero, is the angle in radians between the positive -axis of a plane and the point given by the coordinates on it...
function.
Now consider the first column of a 3×3 rotation matrix,

Although a2+b2 will probably not equal 1, but some value r2 < 1, we can use a slight variation of the previous computation to find a so-called Givens rotation that transforms the column to

zeroing b. This acts on the subspace spanned by the x and y axes. We can then repeat the process for the xz subspace to zero c. Acting on the full matrix, these two rotations produce the schematic form

Shifting attention to the second column, a Givens rotation of the yz subspace can now zero the z value. This brings the full matrix to the form

which is an identity matrix. Thus we have decomposed Q as

An n×n rotation matrix will have (n−1)+(n−2)+⋯+2+1, or

entries below the diagonal to zero. We can zero them by extending the same idea of stepping through the columns with a series of rotations in a fixed sequence of planes. We conclude that the set of n×n rotation matrices, each of which has n2 entries, can be parameterized by n(n−1)/2 angles.
| xzxw | xzyw | xyxw | xyzw |
| yxyw | yxzw | yzyw | yzxw |
| zyzw | zyxw | zxzw | zxyw |
| xzxb | yzxb | xyxb | zyxb |
| yxyb | zxyb | yzyb | xzyb |
| zyzb | xyzb | zxzb | yxzb |
In three dimensions this restates in matrix form an observation made by Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
, so mathematicians call the ordered sequence of three angles Euler angles
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
. However, the situation is somewhat more complicated than we have so far indicated. Despite the small dimension, we actually have considerable freedom in the sequence of axis pairs we use; and we also have some freedom in the choice of angles. Thus we find many different conventions employed when three-dimensional rotations are parameterized for physics, or medicine, or chemistry, or other disciplines. When we include the option of world axes or body axes, 24 different sequences are possible. And while some disciplines call any sequence Euler angles, others give different names (Euler, Cardano, Tait-Bryan, Roll-pitch-yaw) to different sequences.
One reason for the large number of options is that, as noted previously, rotations in three dimensions (and higher) do not commute. If we reverse a given sequence of rotations, we get a different outcome. This also implies that we cannot compose two rotations by adding their corresponding angles. Thus Euler angles are not vectors
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, despite a similarity in appearance as a triple of numbers.
Nested dimensions
A 3×3 rotation matrix like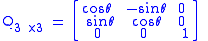
suggests a 2×2 rotation matrix,
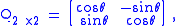
is embedded in the upper left corner:
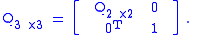
This is no illusion; not just one, but many, copies of n-dimensional rotations are found within (n+1)-dimensional rotations, as subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s. Each embedding leaves one direction fixed, which in the case of 3×3 matrices is the rotation axis. For example, we have
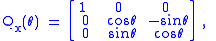
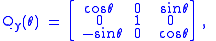
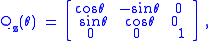
fixing the x axis, the y axis, and the z axis, respectively. The rotation axis need not be a coordinate axis; if u = (x,y,z) is a unit vector in the desired direction, then
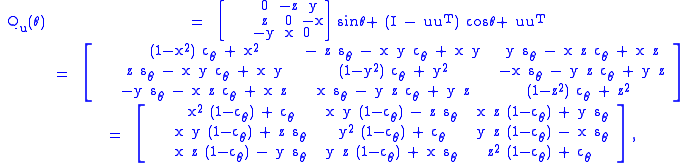
where cθ = cos θ, sθ = sin θ, is a rotation by angle θ leaving axis u fixed.
A direction in (n+1)-dimensional space will be a unit magnitude vector, which we may consider a point on a generalized sphere, Sn. Thus it is natural to describe the rotation group SO(n+1) as combining SO(n) and Sn. A suitable formalism is the fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
,

where for every direction in the "base space", Sn, the "fiber" over it in the "total space", SO(n+1), is a copy of the "fiber space", SO(n), namely the rotations that keep that direction fixed.
Thus we can build an n×n rotation matrix by starting with a 2×2 matrix, aiming its fixed axis on S2 (the ordinary sphere in three-dimensional space), aiming the resulting rotation on S3, and so on up through Sn−1. A point on Sn can be selected using n numbers, so we again have n(n−1)/2 numbers to describe any n×n rotation matrix.
In fact, we can view the sequential angle decomposition, discussed previously, as reversing this process. The composition of n−1 Givens rotations brings the first column (and row) to (1,0,…,0), so that the remainder of the matrix is a rotation matrix of dimension one less, embedded so as to leave (1,0,…,0) fixed.
Skew parameters via Cayley's formula
When an n×n rotation matrix, Q, does not include −1 as an eigenvalue, so that none of the planar rotations of which it is composed are 180° rotations, then Q+I is an invertible matrix. Most rotation matrices fit this description, and for them we can show that (Q−I)(Q+I)−1 is a skew-symmetric matrixSkew-symmetric matrix
In mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...
, A. Thus AT = −A; and since the diagonal is necessarily zero, and since the upper triangle determines the lower one, A contains n(n−1)/2 independent numbers. Conveniently, I−A is invertible whenever A is skew-symmetric; thus we can recover the original matrix using the Cayley transform
Cayley transform
In mathematics, the Cayley transform, named after Arthur Cayley, has a cluster of related meanings. As originally described by , the Cayley transform is a mapping between skew-symmetric matrices and special orthogonal matrices. In complex analysis, the Cayley transform is a conformal mapping in...
,
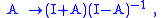
which maps any skew-symmetric matrix A to a rotation matrix. In fact, aside from the noted exceptions, we can produce any rotation matrix in this way. Although in practical applications we can hardly afford to ignore 180° rotations, the Cayley transform is still a potentially useful tool, giving a parameterization of most rotation matrices without trigonometric functions.
In three dimensions, for example, we have
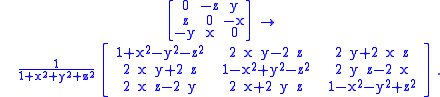
If we condense the skew entries into a vector, (x,y,z), then we produce a 90° rotation around the x axis for (1,0,0), around the y axis for (0,1,0), and around the z axis for (0,0,1). The 180° rotations are just out of reach; for, in the limit as x goes to infinity, (x,0,0) does approach a 180° rotation around the x axis, and similarly for other directions.
Lie group
We have established that n×n rotation matrices form a groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, the special orthogonal group, SO(n). This algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
is coupled with a topological structure, in that the operations of multiplication and taking the inverse (which here is merely transposition) are continuous functions of the matrix entries. Thus SO(n) is a classic example of a topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
. (In purely topological terms, it is a compact manifold.) Furthermore, the operations are not only continuous, but smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
, so SO(n) is a differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
and a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
.
Most properties of rotation matrices depend very little on the dimension, n; yet in Lie group theory we see systematic differences between even dimensions and odd dimensions. As well, there are some irregularities below n = 5; for example, SO(4) is, anomalously, not a simple Lie group
Simple Lie group
In group theory, a simple Lie group is a connected non-abelian Lie group G which does not have nontrivial connected normal subgroups.A simple Lie algebra is a non-abelian Lie algebra whose only ideals are 0 and itself...
, but instead isomorphic to the product
Direct product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
of S3 and SO(3).
Lie algebra
Associated with every Lie group is a Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
, a linear space equipped with a bilinear alternating product is called a bracket. The algebra for SO(n) is denoted by
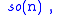
and consists of all skew-symmetric
Skew-symmetric matrix
In mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...
n×n matrices (as implied by differentiating the orthogonality condition
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
, I = QTQ). The bracket, [A1,A2], of two skew-symmetric matrices is defined to be A1A2−A2A1, which is again a skew-symmetric matrix. This Lie algebra bracket captures the essence of the Lie group product via infinitesimals.
For 2×2 rotation matrices, the Lie algebra is a one-dimensional vector space, multiples of
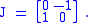
Here the bracket always vanishes, which tells us that, in two dimensions, rotations commute. Not so in any higher dimension. For 3×3 rotation matrices, we have a three-dimensional vector space with the convenient basis
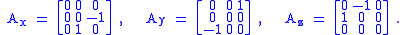
The Lie brackets of these generators are as follows
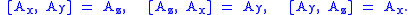
We can conveniently identify any matrix in this Lie algebra with a vector in R3,
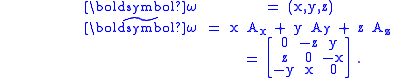
Under this identification, the so(3) bracket has a memorable description; it is the vector cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
,
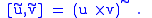
The matrix identified with a vector v is also memorable, because

Notice this implies that v is in the null space
Null space
In linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...
of the skew-symmetric matrix with which it is identified, because v×v is always the zero vector.
Exponential map
Connecting the Lie algebra to the Lie group is the exponential mapExponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
, which we define using the familiar power series for ex ,
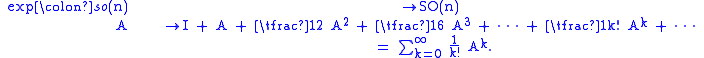
For any skew-symmetric A, exp(A) is always a rotation matrix.
An important practical example is the 3×3 case, where we have seen we can identify every skew-symmetric matrix with a vector ω = uθ, where u = (x,y,z) is a unit magnitude vector. Recall that u is in the null space of the matrix associated with ω, so that if we use a basis with u as the z axis the final column and row will be zero. Thus we know in advance that the exponential matrix must leave u fixed. It is mathematically impossible to supply a straightforward formula for such a basis as a function of u (its existence would violate the hairy ball theorem
Hairy ball theorem
The hairy ball theorem of algebraic topology states that there is no nonvanishing continuous tangent vector field on an even-dimensional n-sphere. An ordinary sphere is a 2-sphere, so that this theorem will hold for an ordinary sphere...
), but direct exponentiation is possible, and yields
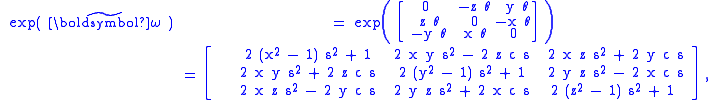
where c = cos θ⁄2, s = sin θ⁄2. We recognize this as our matrix for a rotation around axis u by angle θ. We also note that this mapping of skew-symmetric matrices is quite different from the Cayley transform discussed earlier.
In any dimension, if we choose some nonzero A and consider all its scalar multiples, exponentiation yields rotation matrices along a geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
of the group manifold, forming a one-parameter subgroup of the Lie group. More broadly, the exponential map provides a homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
between a neighborhood of the origin in the Lie algebra and a neighborhood of the identity in the Lie group. In fact, we can produce any rotation matrix as the exponential of some skew-symmetric matrix, so for these groups the exponential map is a surjection.
Baker–Campbell–Hausdorff formula
Suppose we are given A and B in the Lie algebra. Their exponentials, exp(A) and exp(B), are rotation matrices, which we can multiply. Since the exponential map is a surjection, we know that for some C in the Lie algebra, exp(A)exp(B) = exp(C), and we write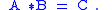
When exp(A) and exp(B) commute (which always happens for 2×2 matrices, but not higher), then C = A+B, mimicking the behavior of complex exponentiation. The general case is given by the BCH formula, a series expanded in terms of the bracket . For matrices, the bracket is the same operation as the commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
, which detects lack of commutativity in multiplication. The general formula begins as follows.
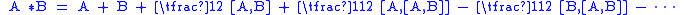
Representation of a rotation matrix as a sequential angle decomposition, as in Euler angles, may tempt us to treat rotations as a vector space, but the higher order terms in the BCH formula reveal that to be a mistake.
We again take special interest in the 3×3 case, where [A,B] equals the cross product, A×B. If A and B are linearly independent, then A, B, and A×B can be used as a basis; if not, then A and B commute. And conveniently, in this dimension the summation in the BCH formula has a closed form as αA+βB+γ(A×B).
Spin group
The Lie group of n×n rotation matrices, SO(n), is a compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
and path-connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, and thus locally compact
Locally compact space
In topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space.-Formal definition:...
and connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
. However, it is not simply connected
Simply connected space
In topology, a topological space is called simply connected if it is path-connected and every path between two points can be continuously transformed, staying within the space, into any other path while preserving the two endpoints in question .If a space is not simply connected, it is convenient...
, so Lie theory tells us it is a kind of "shadow" (a homomorphic image) of a universal covering group
Universal covering group
In mathematics, a covering group of a topological group H is a covering space G of H such that G is a topological group and the covering map p : G → H is a continuous group homomorphism. The map p is called the covering homomorphism...
. Often the covering group, which in this case is the spin group denoted by Spin(n), is simpler and more natural to work with .
In the case of planar rotations, SO(2) is topologically a circle
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
, S1. Its universal covering group, Spin(2), is isomorphic to the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
, R, under addition. In other words, whenever we use angles of arbitrary magnitude, which we often do, we are essentially taking advantage of the convenience of the "mother space". Every 2×2 rotation matrix is produced by a countable infinity of angles, separated by integer multiples of 2π. Correspondingly, the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of SO(2) is isomorphic to the integers, Z.
In the case of spatial rotations, SO(3) is topologically equivalent to three-dimensional real projective space
Real projective space
In mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...
, RP3. Its universal covering group, Spin(3), is isomorphic to the 3-sphere, S3. Every 3×3 rotation matrix is produced by two opposite points on the sphere. Correspondingly, the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of SO(3) is isomorphic to the two-element group, Z2. We can also describe Spin(3) as isomorphic to quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s of unit norm under multiplication, or to certain 4×4 real matrices, or to 2×2 complex special unitary matrices
Special unitary group
The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
.
Concretely, a unit quaternion, q, with
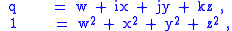
produces the rotation matrix
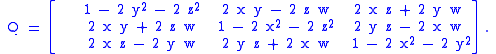
This is our third version of this matrix, here as a rotation around non-unit axis vector (x,y,z) by angle 2θ, where cos θ = w and |sin θ| = ||(x,y,z)||. (The proper sign for sin θ is implied once the signs of the axis components are decided.)
Many features of this case are the same for higher dimensions. The coverings are all two-to-one, with SO(n), n > 2, having fundamental group Z2. The natural setting for these groups is within a Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
. And the action of the rotations is produced by a kind of "sandwich", denoted by qvq∗.
Infinitesimal rotations
The matrices in the Lie algebra are not themselves rotations; the skew-symmetric matrices are derivatives, proportional differences of rotations. An actual "differential rotation", or infinitesimal rotation matrix has the form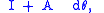
where dθ is vanishingly small. These matrices do not satisfy all the same properties as ordinary finite rotation matrices under the usual treatment of infinitesimals . To understand what this means, consider
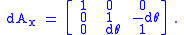
We first test the orthogonality condition, QTQ = I. The product is
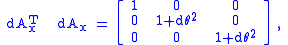
differing from an identity matrix by second order infinitesimals, which we discard. So to first order, an infinitesimal rotation matrix is an orthogonal matrix. Next we examine the square of the matrix.
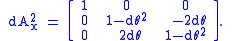
Again discarding second order effects, we see that the angle simply doubles. This hints at the most essential difference in behavior, which we can exhibit with the assistance of a second infinitesimal rotation,
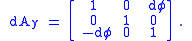
Compare the products dAxdAy and dAydAx.
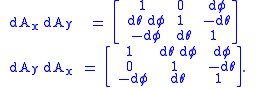
Since dθ dφ is second order, we discard it; thus, to first order, multiplication of infinitesimal rotation matrices is commutative. In fact,

again to first order. Put in other words, the order in which infinitesimal rotations are applied is irrelevant, this useful fact makes, for example, derivation of rigid body rotation relatively simple.
But we must always be careful to distinguish (the first order treatment of) these infinitesimal rotation matrices from both finite rotation matrices and from derivatives of rotation matrices (namely skew-symmetric matrices). Contrast the behavior of finite rotation matrices in the BCH formula with that of infinitesimal rotation matrices, where all the commutator terms will be second order infinitesimals so we do have a vector space.
Conversions
We have seen the existence of several decompositions that apply in any dimension, namely independent planes, sequential angles, and nested dimensions. In all these cases we can either decompose a matrix or construct one. We have also given special attention to 3×3 rotation matrices, and these warrant further attention, in both directions .Quaternion
Given the unit quaternion q = (w,x,y,z), the equivalent 3×3 rotation matrix is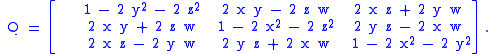
Now every quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
component appears multiplied by two in a term of degree two, and if all such terms are zero what's left is an identity matrix. This leads to an efficient, robust conversion from any quaternion — whether unit, nonunit, or even zero — to a 3×3 rotation matrix.
Nq = w^2 + x^2 + y^2 + z^2
if Nq > 0.0 then s = 2/Nq else s = 0.0
X = x*s; Y = y*s; Z = z*s
wX = w*X; wY = w*Y; wZ = w*Z
xX = x*X; xY = x*Y; xZ = x*Z
yY = y*Y; yZ = y*Z; zZ = z*Z
[ 1.0-(yY+zZ) xY-wZ xZ+wY ]
[ xY+wZ 1.0-(xX+zZ) yZ-wX ]
[ xZ-wY yZ+wX 1.0-(xX+yY) ]
Freed from the demand for a unit quaternion, we find that nonzero quaternions act as homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
for 3×3 rotation matrices. The Cayley transform, discussed earlier, is obtained by scaling the quaternion so that its w component is 1. For a 180° rotation around any axis, w will be zero, which explains the Cayley limitation.
The sum of the entries along the main diagonal (the trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
), plus one, equals 4−4(x2+y2+z2), which is 4w2. Thus we can write the trace itself as 2w2+2w2−1; and from the previous version of the matrix we see that the diagonal entries themselves have the same form: 2x2+2w2−1, 2y2+2w2−1, and 2z2+2w2−1. So we can easily compare the magnitudes of all four quaternion components using the matrix diagonal. We can, in fact, obtain all four magnitudes using sums and square roots, and choose consistent signs using the skew-symmetric part of the off-diagonal entries.
t = Qxx+Qyy+Qzz (trace of Q)
r = sqrt(1+t)
w = 0.5*r
x = copysign(0.5*sqrt(1+Qxx-Qyy-Qzz), Qzy-Qyz)
y = copysign(0.5*sqrt(1-Qxx+Qyy-Qzz), Qxz-Qzx)
z = copysign(0.5*sqrt(1-Qxx-Qyy+Qzz), Qyx-Qxy)
where copysign(x,y) is x with the sign of y:
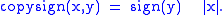
Alternatively, use a single square root and division
t = Qxx+Qyy+Qzz
r = sqrt(1+t)
s = 0.5/r
w = 0.5*r
x = (Qzy-Qyz)*s
y = (Qxz-Qzx)*s
z = (Qyx-Qxy)*s
This is numerically stable so long as the trace, t, is not negative; otherwise, we risk dividing by (nearly) zero. In that case, suppose Qxx is the largest diagonal entry, so x will have the largest magnitude (the other cases are similar); then the following is safe.
t = Qxx+Qyy+Qzz
r = sqrt(1+t)
s = 0.5/r
w = (Qzy-Qyz)*s
x = 0.5*r
y = (Qxy+Qyx)*s
z = (Qzx+Qxz)*s
If the matrix contains significant error, such as accumulated numerical error, we may construct a symmetric 4×4 matrix,
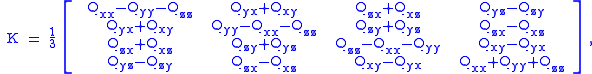
and find the eigenvector, (w,x,y,z), of its largest magnitude eigenvalue. (If Q is truly a rotation matrix, that value will be 1.) The quaternion so obtained will correspond to the rotation matrix closest to the given matrix .
Polar decomposition
If the n×n matrix M is non-singular, its columns are linearly independent vectors; thus the Gram–Schmidt processGram–Schmidt process
In mathematics, particularly linear algebra and numerical analysis, the Gram–Schmidt process is a method for orthonormalising a set of vectors in an inner product space, most commonly the Euclidean space Rn...
can adjust them to be an orthonormal basis. Stated in terms of numerical linear algebra
Numerical linear algebra
Numerical linear algebra is the study of algorithms for performing linear algebra computations, most notably matrix operations, on computers. It is often a fundamental part of engineering and computational science problems, such as image and signal processing, Telecommunication, computational...
, we convert M to an orthogonal matrix, Q, using QR decomposition
QR decomposition
In linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A=QR of an orthogonal matrix Q and an upper triangular matrix R...
. However, we often prefer a Q "closest" to M, which this method does not accomplish. For that, the tool we want is the polar decomposition .
To measure closeness, we may use any matrix norm invariant under orthogonal transformations. A convenient choice is the Frobenius norm, ||Q−M||F, squared, which is the sum of the squares of the element differences. Writing this in terms of the trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
, Tr, our goal is,
- Find Q minimizing Tr( (Q−M)T(Q−M) ), subject to QTQ = I.
Though written in matrix terms, the objective function is just a quadratic polynomial. We can minimize it in the usual way, by finding where its derivative is zero. For a 3×3 matrix, the orthogonality constraint implies six scalar equalities that the entries of Q must satisfy. To incorporate the constraint(s), we may employ a standard technique, Lagrange multipliers
Lagrange multipliers
In mathematical optimization, the method of Lagrange multipliers provides a strategy for finding the maxima and minima of a function subject to constraints.For instance , consider the optimization problem...
, assembled as a symmetric matrix, Y. Thus our method is:
- Differentiate Tr( (Q−M)T(Q−M) + (QTQ−I)Y ) with respect to (the entries of) Q, and equate to zero.
In general, we obtain the equation
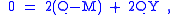
so that
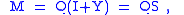
where Q is orthogonal and S is symmetric. To ensure a minimum, the Y matrix (and hence S) must be positive definite. Linear algebra calls QS the polar decomposition of M, with S the positive square root of S2 = MTM.
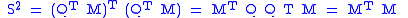
When M is non-singular, the Q and S factors of the polar decomposition are uniquely determined. However, the determinant of S is positive because S is positive definite, so Q inherits the sign of the determinant of M. That is, Q is only guaranteed to be orthogonal, not a rotation matrix. This is unavoidable; an M with negative determinant has no uniquely-defined closest rotation matrix.
Axis and angle
To efficiently construct a rotation matrix Q from an angle θ and a unit axis u, we can take advantage of symmetry and skew-symmetry within the entries. If x, y, and z are the components of the unit vector representing the axis, andc = cos(θ); s = sin(θ); C = 1-c
then Q is
[ xxC+c xyC-zs xzC+ys ]
[ yxC+zs yyC+c yzC-xs ]
[ zxC-ys zyC+xs zzC+c ]
Determining an axis and angle, like determining a quaternion, is only possible up to sign; that is, (u,θ) and (−u,−θ) correspond to the same rotation matrix, just like q and −q. As well, axis-angle extraction presents additional difficulties. The angle can be restricted to be from 0° to 180°, but angles are formally ambiguous by multiples of 360°. When the angle is zero, the axis is undefined. When the angle is 180°, the matrix becomes symmetric, which has implications in extracting the axis. Near multiples of 180°, care is needed to avoid numerical problems: in extracting the angle, a two-argument arctangent
Atan2
In trigonometry, the two-argument function atan2 is a variation of the arctangent function. For any real arguments and not both equal to zero, is the angle in radians between the positive -axis of a plane and the point given by the coordinates on it...
with atan2
Atan2
In trigonometry, the two-argument function atan2 is a variation of the arctangent function. For any real arguments and not both equal to zero, is the angle in radians between the positive -axis of a plane and the point given by the coordinates on it...
(sin θ,cos θ) equal to θ avoids the insensitivity of arccosine; and in computing the axis magnitude to force unit magnitude, a brute-force approach can lose accuracy through underflow .
A partial approach is as follows.
x = Qzy-Qyz
y = Qxz-Qzx
z = Qyx-Qxy
r = sqrt(x2 + y2 + z2)
t = Qxx+Qyy+Qzz (trace of matrix Q)
θ = atan2(r,t−1)
The x, y, and z components of the axis would then be divided by r. A fully robust approach will use different code when the trace t is negative, as with quaternion extraction. When r is zero because the angle is zero, an axis must be provided from some source other than the matrix.
Euler angles
Complexity of conversion escalates with Euler anglesEuler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
(used here in the broad sense). The first difficulty is to establish which of the twenty-four variations of Cartesian axis order we will use. Suppose the three angles are θ1, θ2, θ3; physics and chemistry may interpret these as
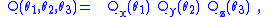
while aircraft dynamics may use
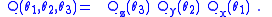
One systematic approach begins with choosing the right-most axis. Among all permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s of (x,y,z), only two place that axis first; one is an even permutation and the other odd. Choosing parity thus establishes the middle axis. That leaves two choices for the left-most axis, either duplicating the first or not. These three choices gives us 3×2×2 = 12 variations; we double that to 24 by choosing static or rotating axes.
This is enough to construct a matrix from angles, but triples differing in many ways can give the same rotation matrix. For example, suppose we use the zyz convention above; then we have the following equivalent pairs:
| (90°, | 45°, | −105°) | ≡ | (−270°, | −315°, | 255°) | multiples of 360° |
| (72°, | 0°, | 0°) | ≡ | (40°, | 0°, | 32°) | singular alignment |
| (45°, | 60°, | −30°) | ≡ | (−135°, | −60°, | 150°) | bistable flip |
Angles for any order can be found using a concise common routine .
The problem of singular alignment, the mathematical analog of physical gimbal lock
Gimbal lock
Gimbal lock is the loss of one degree of freedom in a three-dimensional space that occurs when the axes of two of the three gimbals are driven into a parallel configuration, "locking" the system into rotation in a degenerate two-dimensional space....
, occurs when the middle rotation aligns the axes of the first and last rotations. It afflicts every axis order at either even or odd multiples of 90°. These singularities are not characteristic of the rotation matrix as such, and only occur with the usage of Euler angles.
The singularities are avoided when considering and manipulating the rotation matrix as orthonormal row vectors (in 3D applications often named 'right'-vector, 'up'-vector and 'out'-vector) instead of as angles. The singularities are also avoided when working with quaternions.
Uniform random rotation matrices
We sometimes need to generate a uniformly distributed random rotation matrix. It seems intuitively clear in two dimensions that this means the rotation angle is uniformly distributed between 0 and 2π. That intuition is correct, but does not carry over to higher dimensions. For example, if we decompose 3×3 rotation matrices in axis-angle form, the angle should not be uniformly distributed; the probability that (the magnitude of) the angle is at most θ should be 1⁄π(θ − sin θ), for 0 ≤ θ ≤ π.Since SO(n) is a connected and locally compact Lie group, we have a simple standard criterion for uniformity, namely that the distribution be unchanged when composed with any arbitrary rotation (a Lie group "translation"). This definition corresponds to what is called Haar measure
Haar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
. show how to use the Cayley transform to generate and test matrices according to this criterion.
We can also generate a uniform distribution in any dimension using the subgroup algorithm of . This recursively exploits the nested dimensions group structure of SO(n), as follows. Generate a uniform angle and construct a 2×2 rotation matrix. To step from n to n+1, generate a vector v uniformly distributed on the n-sphere, Sn, embed the n×n matrix in the next larger size with last column (0,…,0,1), and rotate the larger matrix so the last column becomes v.
As usual, we have special alternatives for the 3×3 case. Each of these methods begins with three independent random scalars uniformly distributed on the unit interval. takes advantage of the odd dimension to change a Householder reflection to a rotation by negation, and uses that to aim the axis of a uniform planar rotation.
Another method uses unit quaternions. Multiplication of rotation matrices is homomorphic to multiplication of quaternions, and multiplication by a unit quaternion rotates the unit sphere. Since the homomorphism is a local isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
, we immediately conclude that to produce a uniform distribution on SO(3) we may use a uniform distribution on S3.
Euler angles can also be used, though not with each angle uniformly distributed .
For the axis-angle form, the axis is uniformly distributed over the unit sphere of directions, S2, while the angle has the non-uniform distribution over [0,π] noted previously .
See also
- Rotation operator (vector space)Rotation operator (vector space)This article derives the main properties of rotations in 3-dimensional space.The three Euler rotations are one way to bring a rigid object to any desired orientation by sequentially making rotations about axis' fixed relative to the object. However, this can also be achieved with one single...
- Rotation representation
- Kabsch algorithmKabsch algorithmThe Kabsch algorithm, named after Wolfgang Kabsch, is a method for calculating the optimal rotation matrix that minimizes the RMSD between two paired sets of points...
- IsometryIsometryIn mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
- Orthogonal matrixOrthogonal matrixIn linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
- Rodrigues' rotation formulaRodrigues' rotation formulaIn the theory of three-dimensional rotation, Rodrigues' rotation formula is an efficient algorithm for rotating a vector in space, given an axis and angle of rotation. By extension, this can be used to transform all three basis vectors to compute a rotation matrix from an axis-angle representation...
- Yaw-pitch-roll system
- Plane of rotationPlane of rotationIn geometry, a plane of rotation is an abstract object used to describe or visualise rotations in space. In three dimensions it is an alternative to the axis of rotation, but unlike the axis of rotation it can be used in other dimensions, such as two, four or more dimensions.Mathematically such...
- Transformation matrix
External links
- Rotation matrices at Mathworld
- Math Awareness Month 2000 interactive demo (requires JavaJava (programming language)Java is a programming language originally developed by James Gosling at Sun Microsystems and released in 1995 as a core component of Sun Microsystems' Java platform. The language derives much of its syntax from C and C++ but has a simpler object model and fewer low-level facilities...
) - Rotation Matrices at MathPages A parametrization of SOn(R) by generalized Euler Angles
- Rotation about any point



