
Unitary matrix
Encyclopedia
In mathematics
, a unitary matrix is a (square)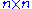 complex
complex
matrix
 satisfying the condition
satisfying the condition

where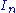 is the identity matrix
is the identity matrix
in n dimensions and is the conjugate transpose
is the conjugate transpose
(also called the Hermitian adjoint
) of . Note this condition implies that a matrix
. Note this condition implies that a matrix  is unitary if and only if it has an inverse which is equal to its conjugate transpose
is unitary if and only if it has an inverse which is equal to its conjugate transpose 
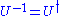
A unitary matrix in which all entries are real is an orthogonal matrix
. Just as an orthogonal matrix preserves the (real
preserves the (real
) inner product of two real
vectors,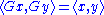
so also a unitary matrix satisfies
satisfies
for all complex vectors x and y, where stands now for the standard inner product on
stands now for the standard inner product on 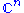 .
.
If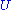 is an
is an  matrix then the following are all equivalent conditions:
matrix then the following are all equivalent conditions:
For any unitary matrix , the following hold:
, the following hold:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a unitary matrix is a (square)
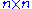 complex
complexComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
 satisfying the condition
satisfying the condition
where
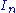 is the identity matrix
is the identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
in n dimensions and
 is the conjugate transpose
is the conjugate transposeConjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
(also called the Hermitian adjoint
Hermitian adjoint
In mathematics, specifically in functional analysis, each linear operator on a Hilbert space has a corresponding adjoint operator.Adjoints of operators generalize conjugate transposes of square matrices to infinite-dimensional situations...
) of
 . Note this condition implies that a matrix
. Note this condition implies that a matrix  is unitary if and only if it has an inverse which is equal to its conjugate transpose
is unitary if and only if it has an inverse which is equal to its conjugate transpose 
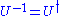
A unitary matrix in which all entries are real is an orthogonal matrix
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
. Just as an orthogonal matrix
 preserves the (real
preserves the (realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
) inner product of two real
vectors,
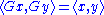
so also a unitary matrix
 satisfies
satisfies
for all complex vectors x and y, where
 stands now for the standard inner product on
stands now for the standard inner product on 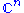 .
.If
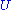 is an
is an  matrix then the following are all equivalent conditions:
matrix then the following are all equivalent conditions:
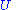 is unitary
is unitary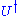 is unitary
is unitary- the columns of
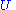 form an orthonormal basisOrthonormal basisIn mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
form an orthonormal basisOrthonormal basisIn mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
of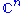 with respect to this inner product
with respect to this inner product - the rows of
 form an orthonormal basis of
form an orthonormal basis of 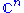 with respect to this inner product
with respect to this inner product -
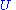 is an isometryIsometryIn mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
is an isometryIsometryIn mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
with respect to the norm from this inner product -
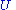 is a normal matrixNormal matrixA complex square matrix A is a normal matrix ifA^*A=AA^* \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT...
is a normal matrixNormal matrixA complex square matrix A is a normal matrix ifA^*A=AA^* \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT...
with eigenvalues lying on the unit circleUnit circleIn mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
.
Properties
- All unitary matrices are normalNormal matrixA complex square matrix A is a normal matrix ifA^*A=AA^* \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT...
, and the spectral theoremSpectral theoremIn mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
therefore applies to them. Thus every unitary matrix has a decomposition of the form
has a decomposition of the form
- where
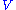 is unitary, and
is unitary, and  is diagonal and unitary. That is, a unitary matrix is diagonalizableDiagonalizable matrixIn linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
is diagonal and unitary. That is, a unitary matrix is diagonalizableDiagonalizable matrixIn linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
by a unitary matrix.
For any unitary matrix
 , the following hold:
, the following hold:
-
 .
. -
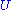 is invertible, with
is invertible, with  .
. -
 is also unitary.
is also unitary. -
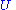 preserves length ("isometryIsometryIn mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
preserves length ("isometryIsometryIn mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
"):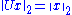 .
. - if
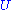 has complex eigenvalues, they are of modulus 1.
has complex eigenvalues, they are of modulus 1. - Eigenspaces are Orthogonal: If matrix is normal then its eigenvectors corresponding to different eigenvalues are orthogonal.
- For any n, the set of all n by n unitary matrices with matrix multiplication forms a groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, called U(n)Unitary groupIn mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
. - Any unit-norm matrix is the average of two unitary matrices. As a consequence, every
 matrix
matrix  is a linear combination of two unitary matrices.
is a linear combination of two unitary matrices.
See also
- Orthogonal matrixOrthogonal matrixIn linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
- Hermitian matrix
- Symplectic matrix
- Unitary groupUnitary groupIn mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
- Special unitary groupSpecial unitary groupThe special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
- Unitary operatorUnitary operatorIn functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
- Matrix decompositionMatrix decompositionIn the mathematical discipline of linear algebra, a matrix decomposition is a factorization of a matrix into some canonical form. There are many different matrix decompositions; each finds use among a particular class of problems.- Example :...
- Identity matrixIdentity matrixIn linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...


