
Alexander polynomial
Encyclopedia
In mathematics
, the Alexander polynomial is a knot invariant
which assigns a polynomial
with integer coefficients to each knot type. James Waddell Alexander II
discovered this, the first knot polynomial
, in 1923. In 1969, John Conway
showed a version of this polynomial, now called the Alexander–Conway polynomial, could be computed using a skein relation
, although its significance was not realized until the discovery of the Jones polynomial in 1984. Soon after Conway's reworking of the Alexander polynomial, it was realized that a similar skein relation was exhibited in Alexander's paper on his polynomial.
. Let X be the infinite cyclic cover of the knot complement
of K. This covering can be obtained by cutting the knot complement along a Seifert surface
of K and gluing together infinitely many copies of the resulting manifold with boundary in a cyclic manner. There is a covering transformation t acting on X. Consider the first homology (with integer coefficients) of X, denoted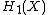 . The transformation t acts on the homology and so we can consider
. The transformation t acts on the homology and so we can consider  a module
a module
over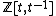 . This is called the Alexander invariant or Alexander module.
. This is called the Alexander invariant or Alexander module.
The module is finitely presentable; a presentation matrix for this module is called the Alexander matrix. If the number of generators, r, is less than or equal to the number of relations, s, then we consider the ideal generated by all r by r minors of the matrix; this is the zero'th Fitting ideal
or Alexander ideal and does not depend on choice of presentation matrix. If r > s, set the ideal equal to 0. If the Alexander ideal is principal
, take a generator; this is called an Alexander polynomial of the knot. Since this is only unique up to multiplication by the Laurent monomial , one often fixes a particular unique form. Alexander's choice of normalization is to make the polynomial have a positive constant term
, one often fixes a particular unique form. Alexander's choice of normalization is to make the polynomial have a positive constant term
.
Alexander proved that the Alexander ideal is nonzero and always principal. Thus an Alexander polynomial always exists, and is clearly a knot invariant, denoted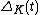 .
.
Take an oriented diagram of the knot with n crossings; there are n + 2 regions of the knot diagram. To work out the Alexander polynomial, first one must create an incidence matrix
of size (n, n + 2). The n rows correspond to the n crossings, and the n + 2 columns to the regions. The values for the matrix entries are either 0, 1, −1, t, −t.
Consider the entry corresponding to a particular region and crossing. If the region is not adjacent to the crossing, the entry is 0. If the region is adjacent to the crossing, the entry depends on its location. The following table gives the entry, determined by the location of the region at the crossing from the perspective of the incoming undercrossing line.
Remove two columns corresponding to adjacent regions from the matrix, and work out the determinant of the new n by n matrix. Depending on the columns removed, the answer will differ by multiplication by . To resolve this ambiguity, divide out the largest possible power of t and multiply by −1 if necessary, so that the constant term is positive. This gives the Alexander polynomial.
. To resolve this ambiguity, divide out the largest possible power of t and multiply by −1 if necessary, so that the constant term is positive. This gives the Alexander polynomial.
The Alexander polynomial can also be computed from the Seifert matrix.
 for all k a knot
for all k a knot
and it evaluates to a unit on 1: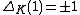 .
.
It is known that every integral Laurent polynomial which is both symmetric and evaluates to a unit at 1 is the Alexander polynomial of a knot (Kawauchi 1996).
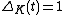 if and only if
if and only if
the commutator subgroup of the knot group is perfect
(i.e. equal to its own commutator subgroup).
For a topologically slice knot, the Alexander polynomial satisfies the Fox–Milnor condition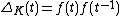 where
where 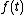 is some other integral Laurent polynomial.
is some other integral Laurent polynomial.
Twice the knot genus
is bounded below by the degree of the Alexander polynomial.
Michael Freedman proved that a knot in the 3-sphere is topologically slice; i.e., bounds a "locally-flat" topological disc in the 4-ball, if the Alexander polynomial of the knot is trivial (Freedman and Quinn, 1990).
There are other relations with surfaces and smooth 4-dimensional topology. For example, under certain assumptions, there is a way of modifying a smooth 4-manifold
by performing a surgery
that consists of removing a neighborhood of a two-dimensional torus and replacing it with a knot complement crossed with S1. The result is a smooth 4-manifold homeomorphic to the original, though now the Seiberg–Witten invariant has been modified by multiplication with the Alexander polynomial of the knot.
Knots with symmetries are known to have restricted Alexander polynomials. See the symmetry section in (Kawauchi 1996). Although, the Alexander polynomial can fail to detect some symmetries, such as strong invertibility.
If the knot complement
fibers over the circle, then the Alexander polynomial of the knot is known to be monic (highest and lowest order terms equal to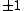 ). In fact, if
). In fact, if  is a fiber bundle where
is a fiber bundle where 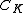 is the knot complement, let
is the knot complement, let 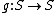 represent the monodromy
represent the monodromy
, then where
where 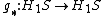 is the induced map on homology.
is the induced map on homology.
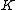 is a satellite knot
is a satellite knot
with companion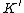 i.e.: there exists an embedding
i.e.: there exists an embedding 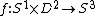 such that
such that 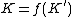 where
where 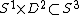 is an unknotted solid torus, then
is an unknotted solid torus, then 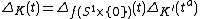 . Where
. Where 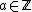 is the integer that represents
is the integer that represents 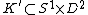 in
in 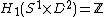 .
.
Examples: For a connect-sum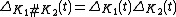 . If
. If 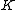 is an untwisted Whitehead double, then
is an untwisted Whitehead double, then 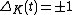 .
.
later rediscovered this in a different form and showed that the skein relation together with a choice of value on the unknot was enough to determine the polynomial. Conway's version is a polynomial in z with integer coefficients, denoted and called the Alexander–Conway polynomial (also known as Conway polynomial or Conway–Alexander polynomial).
and called the Alexander–Conway polynomial (also known as Conway polynomial or Conway–Alexander polynomial).
Suppose we are given an oriented link diagram, where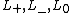 are link diagrams resulting crossing and smoothing changes on a local region of a specified crossing of the diagram, as indicated in the figure.
are link diagrams resulting crossing and smoothing changes on a local region of a specified crossing of the diagram, as indicated in the figure. .svg.png) Here are Conway's skein relations:
Here are Conway's skein relations:
The relationship to the standard Alexander polynomial is given by . Here
. Here 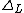 must be properly normalized (by multiplication of
must be properly normalized (by multiplication of 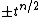 ) to satisfy the skein relation
) to satisfy the skein relation 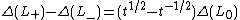 . Note that this relation gives a Laurent polynomial in t1/2.
. Note that this relation gives a Laurent polynomial in t1/2.
See knot theory
for an example computing the Conway polynomial of the trefoil.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Alexander polynomial is a knot invariant
Knot invariant
In the mathematical field of knot theory, a knot invariant is a quantity defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers, but invariants can range from the...
which assigns a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
with integer coefficients to each knot type. James Waddell Alexander II
James Waddell Alexander II
James Waddell Alexander II was a mathematician and topologist of the pre-World War II era and part of an influential Princeton topology elite, which included Oswald Veblen, Solomon Lefschetz, and others...
discovered this, the first knot polynomial
Knot polynomial
In the mathematical field of knot theory, a knot polynomial is a knot invariant in the form of a polynomial whose coefficients encode some of the properties of a given knot.-History:The first knot polynomial, the Alexander polynomial, was introduced by J. W...
, in 1923. In 1969, John Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
showed a version of this polynomial, now called the Alexander–Conway polynomial, could be computed using a skein relation
Skein relation
A central question in the mathematical theory of knots is whether two knot diagrams represent the same knot. One tool used to answer such questions is a knot polynomial which is an invariant of the knot. If two diagrams have different polynomials, they represent different knots. The reverse may not...
, although its significance was not realized until the discovery of the Jones polynomial in 1984. Soon after Conway's reworking of the Alexander polynomial, it was realized that a similar skein relation was exhibited in Alexander's paper on his polynomial.
Definition
Let K be a knot in the 3-sphere3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
. Let X be the infinite cyclic cover of the knot complement
Knot complement
In mathematics, the knot complement of a tame knot K is the complement of the interior of the embedding of a solid torus into the 3-sphere. To make this precise, suppose that K is a knot in a three-manifold M. Let N be a thickened neighborhood of K; so N is a solid torus...
of K. This covering can be obtained by cutting the knot complement along a Seifert surface
Seifert surface
In mathematics, a Seifert surface is a surface whose boundary is a given knot or link.Such surfaces can be used to study the properties of the associated knot or link. For example, many knot invariants are most easily calculated using a Seifert surface...
of K and gluing together infinitely many copies of the resulting manifold with boundary in a cyclic manner. There is a covering transformation t acting on X. Consider the first homology (with integer coefficients) of X, denoted
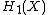 . The transformation t acts on the homology and so we can consider
. The transformation t acts on the homology and so we can consider  a module
a moduleModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over
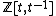 . This is called the Alexander invariant or Alexander module.
. This is called the Alexander invariant or Alexander module.The module is finitely presentable; a presentation matrix for this module is called the Alexander matrix. If the number of generators, r, is less than or equal to the number of relations, s, then we consider the ideal generated by all r by r minors of the matrix; this is the zero'th Fitting ideal
Fitting ideal
In commutative algebra, the Fitting ideals of a finitely generated module over a commutative ring describe the obstructions to generating the module by a given number of elements...
or Alexander ideal and does not depend on choice of presentation matrix. If r > s, set the ideal equal to 0. If the Alexander ideal is principal
Principal ideal
In ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
, take a generator; this is called an Alexander polynomial of the knot. Since this is only unique up to multiplication by the Laurent monomial
 , one often fixes a particular unique form. Alexander's choice of normalization is to make the polynomial have a positive constant term
, one often fixes a particular unique form. Alexander's choice of normalization is to make the polynomial have a positive constant termConstant term
In mathematics, a constant term is a term in an algebraic expression has a value that is constant or cannot change, because it does not contain any modifiable variables. For example, in the quadratic polynomialx^2 + 2x + 3,\ the 3 is a constant term....
.
Alexander proved that the Alexander ideal is nonzero and always principal. Thus an Alexander polynomial always exists, and is clearly a knot invariant, denoted
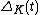 .
.Computing the polynomial
The following procedure for computing the Alexander polynomial was given by J. W. Alexander in his paper.Take an oriented diagram of the knot with n crossings; there are n + 2 regions of the knot diagram. To work out the Alexander polynomial, first one must create an incidence matrix
Incidence matrix
In mathematics, an incidence matrix is a matrix that shows the relationship between two classes of objects. If the first class is X and the second is Y, the matrix has one row for each element of X and one column for each element of Y. The entry in row x and column y is 1 if x and y are related ...
of size (n, n + 2). The n rows correspond to the n crossings, and the n + 2 columns to the regions. The values for the matrix entries are either 0, 1, −1, t, −t.
Consider the entry corresponding to a particular region and crossing. If the region is not adjacent to the crossing, the entry is 0. If the region is adjacent to the crossing, the entry depends on its location. The following table gives the entry, determined by the location of the region at the crossing from the perspective of the incoming undercrossing line.
- on the left before undercrossing: −t
- on the right before undercrossing: 1
- on the left after undercrossing: t
- on the right after undercrossing: −1
Remove two columns corresponding to adjacent regions from the matrix, and work out the determinant of the new n by n matrix. Depending on the columns removed, the answer will differ by multiplication by
 . To resolve this ambiguity, divide out the largest possible power of t and multiply by −1 if necessary, so that the constant term is positive. This gives the Alexander polynomial.
. To resolve this ambiguity, divide out the largest possible power of t and multiply by −1 if necessary, so that the constant term is positive. This gives the Alexander polynomial.The Alexander polynomial can also be computed from the Seifert matrix.
Basic properties of the polynomial
The Alexander polynomial is symmetric: for all k a knot
for all k a knot- From the point of view of the definition, this is an expression of the Poincaré Duality isomorphism
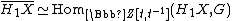 where
where 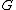 is the quotient of the field of fractions of
is the quotient of the field of fractions of  by
by 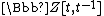 , considered as a
, considered as a 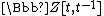 -module, and where
-module, and where 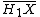 is the conjugate
is the conjugate  -module to
-module to 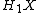 ie: as an abelian group it is identical to
ie: as an abelian group it is identical to  but the covering transformation
but the covering transformation  acts by
acts by  .
.
and it evaluates to a unit on 1:
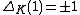 .
.- From the point of view of the definition, this is an expression of the fact that the knot complement is a homology circle, generated by the covering transformation
 . More generally if
. More generally if 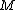 is a 3-manifold such that
is a 3-manifold such that 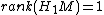 it has an Alexander polynomial
it has an Alexander polynomial 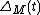 defined as the order ideal of its infinite-cyclic covering space. In this case
defined as the order ideal of its infinite-cyclic covering space. In this case 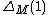 is, up to sign, equal to the order of the torsion subgroup of
is, up to sign, equal to the order of the torsion subgroup of 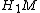 .
.
It is known that every integral Laurent polynomial which is both symmetric and evaluates to a unit at 1 is the Alexander polynomial of a knot (Kawauchi 1996).
Geometric significance of the polynomial
Since the Alexander ideal is principal,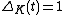 if and only if
if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the commutator subgroup of the knot group is perfect
Perfect group
In mathematics, more specifically in the area of modern algebra known as group theory, a group is said to be perfect if it equals its own commutator subgroup, or equivalently, if the group has no nontrivial abelian quotients...
(i.e. equal to its own commutator subgroup).
For a topologically slice knot, the Alexander polynomial satisfies the Fox–Milnor condition
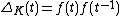 where
where 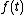 is some other integral Laurent polynomial.
is some other integral Laurent polynomial.Twice the knot genus
Seifert surface
In mathematics, a Seifert surface is a surface whose boundary is a given knot or link.Such surfaces can be used to study the properties of the associated knot or link. For example, many knot invariants are most easily calculated using a Seifert surface...
is bounded below by the degree of the Alexander polynomial.
Michael Freedman proved that a knot in the 3-sphere is topologically slice; i.e., bounds a "locally-flat" topological disc in the 4-ball, if the Alexander polynomial of the knot is trivial (Freedman and Quinn, 1990).
There are other relations with surfaces and smooth 4-dimensional topology. For example, under certain assumptions, there is a way of modifying a smooth 4-manifold
4-manifold
In mathematics, 4-manifold is a 4-dimensional topological manifold. A smooth 4-manifold is a 4-manifold with a smooth structure. In dimension four, in marked contrast with lower dimensions, topological and smooth manifolds are quite different...
by performing a surgery
Surgery theory
In mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...
that consists of removing a neighborhood of a two-dimensional torus and replacing it with a knot complement crossed with S1. The result is a smooth 4-manifold homeomorphic to the original, though now the Seiberg–Witten invariant has been modified by multiplication with the Alexander polynomial of the knot.
Knots with symmetries are known to have restricted Alexander polynomials. See the symmetry section in (Kawauchi 1996). Although, the Alexander polynomial can fail to detect some symmetries, such as strong invertibility.
If the knot complement
Knot complement
In mathematics, the knot complement of a tame knot K is the complement of the interior of the embedding of a solid torus into the 3-sphere. To make this precise, suppose that K is a knot in a three-manifold M. Let N be a thickened neighborhood of K; so N is a solid torus...
fibers over the circle, then the Alexander polynomial of the knot is known to be monic (highest and lowest order terms equal to
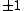 ). In fact, if
). In fact, if  is a fiber bundle where
is a fiber bundle where 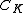 is the knot complement, let
is the knot complement, let 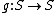 represent the monodromy
represent the monodromyMonodromy
In mathematics, monodromy is the study of how objects from mathematical analysis, algebraic topology and algebraic and differential geometry behave as they 'run round' a singularity. As the name implies, the fundamental meaning of monodromy comes from 'running round singly'...
, then
 where
where 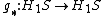 is the induced map on homology.
is the induced map on homology.Relations to satellite operations
If a knot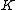 is a satellite knot
is a satellite knotSatellite knot
In the mathematical theory of knots, a satellite knot is a knot that contains an incompressible, non-boundary parallel torus in its complement. The class of satellite knots include composite knots, cable knots and Whitehead doubles. A satellite knot K can be picturesquely described as follows:...
with companion
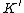 i.e.: there exists an embedding
i.e.: there exists an embedding 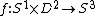 such that
such that 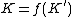 where
where 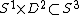 is an unknotted solid torus, then
is an unknotted solid torus, then 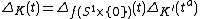 . Where
. Where 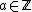 is the integer that represents
is the integer that represents 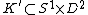 in
in 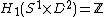 .
.Examples: For a connect-sum
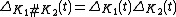 . If
. If 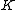 is an untwisted Whitehead double, then
is an untwisted Whitehead double, then 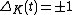 .
.Alexander–Conway polynomial
Alexander proved the Alexander polynomial satisfies a skein relation. John ConwayJohn Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
later rediscovered this in a different form and showed that the skein relation together with a choice of value on the unknot was enough to determine the polynomial. Conway's version is a polynomial in z with integer coefficients, denoted
 and called the Alexander–Conway polynomial (also known as Conway polynomial or Conway–Alexander polynomial).
and called the Alexander–Conway polynomial (also known as Conway polynomial or Conway–Alexander polynomial).Suppose we are given an oriented link diagram, where
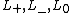 are link diagrams resulting crossing and smoothing changes on a local region of a specified crossing of the diagram, as indicated in the figure.
are link diagrams resulting crossing and smoothing changes on a local region of a specified crossing of the diagram, as indicated in the figure. .svg.png)
-
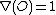 (where O is any diagram of the unknot)
(where O is any diagram of the unknot) -

The relationship to the standard Alexander polynomial is given by
 . Here
. Here 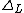 must be properly normalized (by multiplication of
must be properly normalized (by multiplication of 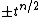 ) to satisfy the skein relation
) to satisfy the skein relation 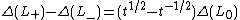 . Note that this relation gives a Laurent polynomial in t1/2.
. Note that this relation gives a Laurent polynomial in t1/2.See knot theory
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
for an example computing the Conway polynomial of the trefoil.
External links
- Knot Atlas – knot and link tables with computed Alexander and Conway polynomials

