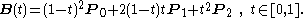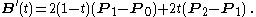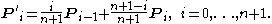Bézier curve
Encyclopedia
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
and related fields. Generalizations of Bézier curves to higher dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s are called Bézier surface
Bézier surface
Bézier surfaces are a species of mathematical spline used in computer graphics, computer-aided design, and finite element modeling.As with the Bézier curve, a Bézier surface is defined by a set of control points...
s, of which the Bézier triangle is a special case.
In vector graphics
Vector graphics
Vector graphics is the use of geometrical primitives such as points, lines, curves, and shapes or polygon, which are all based on mathematical expressions, to represent images in computer graphics...
, Bézier curves are used to model smooth curves that can be scaled indefinitely. "Paths," as they are commonly referred to in image manipulation programs,Image manipulation programs such as Inkscape
Inkscape
Inkscape is a free software vector graphics editor, licensed under the GNU General Public License. Its goal is to implement full support for the Scalable Vector Graphics 1.1 standard....
, Adobe Photoshop
Adobe Photoshop
Adobe Photoshop is a graphics editing program developed and published by Adobe Systems Incorporated.Adobe's 2003 "Creative Suite" rebranding led to Adobe Photoshop 8's renaming to Adobe Photoshop CS. Thus, Adobe Photoshop CS5 is the 12th major release of Adobe Photoshop...
, and GIMP
GIMP
GIMP is a free software raster graphics editor. It is primarily employed as an image retouching and editing tool and is freely available in versions tailored for most popular operating systems including Microsoft Windows, Apple Mac OS X, and Linux.In addition to detailed image retouching and...
. are combinations of linked Bézier curves. Paths are not bound by the limits of rasterized images and are intuitive to modify. Bézier curves are also used in animation
Animation
Animation is the rapid display of a sequence of images of 2-D or 3-D artwork or model positions in order to create an illusion of movement. The effect is an optical illusion of motion due to the phenomenon of persistence of vision, and can be created and demonstrated in several ways...
as a tool to control motion.In animation applications such as Adobe Flash
Adobe Flash
Adobe Flash is a multimedia platform used to add animation, video, and interactivity to web pages. Flash is frequently used for advertisements, games and flash animations for broadcast...
, Adobe After Effects
Adobe After Effects
Adobe After Effects is a digital motion graphics and compositing software published by Adobe Systems, used in the post-production process of filmmaking and television production. Its main uses are the origination of 2D and 2.5D animation, visual effects compositing and finishing...
, Microsoft Expression Blend, Blender
Blender (software)
Blender is a free and open-source 3D computer graphics software product used for creating animated films, visual effects, interactive 3D applications or video games. The current release version is 2.60, and was released on October 19, 2011...
, Autodesk Maya and Autodesk 3ds max.
Bézier curves are also used in the time domain, particularly in animation and interface design, e.g., a Bézier curve can be used to specify the velocity over time of an object such as an icon moving from A to B, rather than simply moving at a fixed number of pixels per step. When animators or interface
Graphical user interface
In computing, a graphical user interface is a type of user interface that allows users to interact with electronic devices with images rather than text commands. GUIs can be used in computers, hand-held devices such as MP3 players, portable media players or gaming devices, household appliances and...
designers talk about the "physics" or "feel" of an operation, they may be referring to the particular Bézier curve used to control the velocity over time of the move in question.
Bézier curves were widely publicized in 1962 by the French
France
The French Republic , The French Republic , The French Republic , (commonly known as France , is a unitary semi-presidential republic in Western Europe with several overseas territories and islands located on other continents and in the Indian, Pacific, and Atlantic oceans. Metropolitan France...
engineer Pierre Bézier
Pierre Bézier
Pierre Étienne Bézier was a French engineer and one of the founders of the fields of solid, geometric and physical modeling as well as in the field of representing curves, especially in CAD/CAM systems...
, who used them to design automobile
Automobile
An automobile, autocar, motor car or car is a wheeled motor vehicle used for transporting passengers, which also carries its own engine or motor...
bodies. The curves were first developed in 1959 by Paul de Casteljau
Paul de Casteljau
Paul de Casteljau is a French physicist and mathematician. In 1959, while working at Citroën, he developed an algorithm for computation of Bézier curves, which would later be formalized and popularized by engineer Pierre Bézier...
using de Casteljau's algorithm
De Casteljau's algorithm
In the mathematical field of numerical analysis, De Casteljau's algorithm is a recursive method to evaluate polynomials in Bernstein form or Bézier curves, named after its inventor Paul de Casteljau...
, a numerically stable
Numerical stability
In the mathematical subfield of numerical analysis, numerical stability is a desirable property of numerical algorithms. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm....
method to evaluate Bézier curves.
Computer graphics

Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of its control points, the points can be graphically displayed and used to manipulate the curve intuitively. Affine transformation
Affine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
s such as translation
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
, and rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
can be applied on the curve by applying the respective transform on the control points of the curve.
Quadratic and cubic Bézier curves are most common; higher degree curves are more expensive to evaluate. When more complex shapes are needed, low order Bézier curves are patched together. This is commonly referred to as a "path" in vector graphics
Vector graphics
Vector graphics is the use of geometrical primitives such as points, lines, curves, and shapes or polygon, which are all based on mathematical expressions, to represent images in computer graphics...
standards (like SVG) and vector graphics programs (like Adobe Illustrator
Adobe Illustrator
Adobe Illustrator is a vector graphics editor developed and marketed by Adobe Systems. Illustrator is similar in scope, intended market, and functionality to its competitors, CorelDraw, Xara Designer Pro and Macromedia FreeHand....
and Inkscape
Inkscape
Inkscape is a free software vector graphics editor, licensed under the GNU General Public License. Its goal is to implement full support for the Scalable Vector Graphics 1.1 standard....
). To guarantee smoothness, the control point at which two curves meet must be on the line between the two control points on either side.
The simplest method for scan converting (rasterizing
Rasterisation
Rasterisation is the task of taking an image described in a vector graphics format and converting it into a raster image for output on a video display or printer, or for storage in a bitmap file format....
) a Bézier curve is to evaluate it at many closely spaced points and scan convert the approximating sequence of line segments. However, this does not guarantee that the rasterized output looks sufficiently smooth, because the points may be spaced too far apart. Conversely it may generate too many points in areas where the curve is close to linear. A common adaptive method is recursive subdivision, in which a curve's control points are checked to see if the curve approximates a line segment to within a small tolerance. If not, the curve is subdivided parametrically into two segments, 0 ≤ t ≤ 0.5 and 0.5 ≤ t ≤ 1, and the same procedure is applied recursively to each half. There are also forward differencing methods, but great care must be taken to analyse error propagation. Analytical methods where a spline
Spline (mathematics)
In mathematics, a spline is a sufficiently smooth piecewise-polynomial function. In interpolating problems, spline interpolation is often preferred to polynomial interpolation because it yields similar results, even when using low-degree polynomials, while avoiding Runge's phenomenon for higher...
is intersected with each scan line involve finding roots of cubic polynomials (for cubic splines) and dealing with multiple roots, so they are not often used in practice.
Animation
In animation applications, such as Adobe FlashAdobe Flash
Adobe Flash is a multimedia platform used to add animation, video, and interactivity to web pages. Flash is frequently used for advertisements, games and flash animations for broadcast...
and Synfig
Synfig
Synfig Studio is a free and open source 2D vector graphics and timeline-based computer animation program created by Robert Quattlebaum with additional contributions by Adrian Bentley....
, Bézier curves are used to outline, for example, movement. Users outline the wanted path in Bézier curves, and the application creates the needed frames for the object to move along the path.
For 3D animation Bézier curves are often used to define 3D paths as well as 2D curves for keyframe interpolation.
Fonts
TrueTypeTrueType
TrueType is an outline font standard originally developed by Apple Computer in the late 1980s as a competitor to Adobe's Type 1 fonts used in PostScript...
fonts use Bézier spline
Bézier spline
In the mathematical field of numerical analysis and in computer graphics, a Bézier spline is a spline curve where each polynomial of the spline is in Bézier form....
s composed of quadratic Bézier curves. Modern imaging systems like PostScript
PostScript
PostScript is a dynamically typed concatenative programming language created by John Warnock and Charles Geschke in 1982. It is best known for its use as a page description language in the electronic and desktop publishing areas. Adobe PostScript 3 is also the worldwide printing and imaging...
, Asymptote
Asymptote (vector graphics language)
Asymptote is a descriptive vector graphics language, developed by Andy Hammerlindl, John C. Bowman , and Tom Prince, that provides a natural coordinate-based framework for technical drawing. Asymptote runs on all major platforms...
, Metafont
METAFONT
Metafont is a programming language used to define vector fonts. It is also the name of the interpreter that executes Metafont code, generating the bitmap fonts that can be embedded into e.g. PostScript...
, and SVG use Bézier spline
Bézier spline
In the mathematical field of numerical analysis and in computer graphics, a Bézier spline is a spline curve where each polynomial of the spline is in Bézier form....
s composed of cubic Bézier curves for drawing curved shapes. OpenType
OpenType
OpenType is a format for scalable computer fonts. It was built on its predecessor TrueType, retaining TrueType's basic structure and adding many intricate data structures for prescribing typographic behavior...
fonts can use either types, depending on the flavor of the font.
The internal rendering of all Bézier curves in font or vector graphics renderers will split them recursively up to the point where the curve is flat enough to be drawn as a series of linear or circular segments. The exact splitting algorithm is implementation dependent, only the flatness criteria must be respected to reach the necessary precision and to avoid non-monotonic local changes of curvature. The "smooth curve" feature of charts in Microsoft Excel
Microsoft Excel
Microsoft Excel is a proprietary commercial spreadsheet application written and distributed by Microsoft for Microsoft Windows and Mac OS X. It features calculation, graphing tools, pivot tables, and a macro programming language called Visual Basic for Applications...
also use this algorithm.
Because arcs of circles and ellipses cannot be exactly represented by Bézier curves, they are first approximated by Bézier curves, which are in turn approximated by arcs of circles. This is inefficient as there exists also approximations of all Bézier curves using arcs of circles or ellipses, which can be rendered incrementally with arbitrary precision. Another approach, used by modern hardware graphics adapters with accelerated geometry, can convert exactly all Bézier and conic curves (or surfaces) into NURBS, that can be rendered incrementally without first splitting the curve recursively to reach the necessary flatness condition. This approach also allows preserving the curve definition under all linear or perspective 2D and 3D transforms and projections.
Font engines, like FreeType
FreeType
FreeType is a software library written in C that implements a font rasterization engine. It is used to render text on to bitmaps and provides support for other font-related operations.-Details:...
, draw the font's curves (and lines) on a pixellated surface, in a process called Font rasterization
Font rasterization
Font rasterization is the process of converting text from a vector description to a raster or bitmap description. This often involves some anti-aliasing on screen text to make it smoother and easier to read...
.
Examination of cases
A Bézier curve is defined by a set of control points P0 through Pn, where n is called its order (n = 1 for linear, 2 for quadratic, etc.). The first and last control points are always the end points of the curve; however, the intermediate control points (if any) generally do not lie on the curve.Linear Bézier curves
Given points P0 and P1, a linear Bézier curve is simply a straight line between those two points. The curve is given by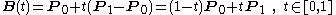
and is equivalent to linear interpolation
Linear interpolation
Linear interpolation is a method of curve fitting using linear polynomials. Lerp is an abbreviation for linear interpolation, which can also be used as a verb .-Linear interpolation between two known points:...
.
Quadratic Bézier curves
A quadratic Bézier curve is the path traced by the function B(t), given points P0, P1, and P2,-
 ,
,
which can be interpreted as the linear interpolant of corresponding points on the linear Bézier curves from P0 to P1 and from P1 to P2 respectively. More explicitly it can be written as:
It departs from P0 in the direction of P1, then bends to arrive at P2 in the direction from P1. In other words, the tangents in P0 and P2 both pass through P1. This is directly seen from the derivative of the Bézier curve:
A quadratic Bézier curve is also a parabolic
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
segment. As a parabola is a conic section
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
, some sources refer to quadratic Béziers as "conic arcs".
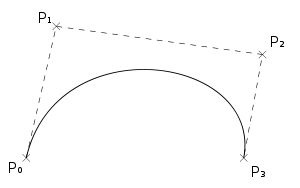
Cubic Bézier curves
Four points P0, P1, P2 and P3 in the plane or in higher-dimensional space define a cubic Bézier curve.The curve starts at P0 going toward P1 and arrives at P3 coming from the direction of P2. Usually, it will not pass through P1 or P2; these points are only there to provide directional information. The distance between P0 and P1 determines "how long" the curve moves into direction P2 before turning towards P3.
Writing BPi,Pj,Pk(t) for the quadratic Bézier curve defined by points Pi, Pj, and Pk, the cubic Bézier curve can be defined as a linear combination of two quadratic Bézier curves:
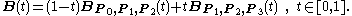
The explicit form of the curve is:
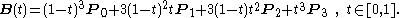
For some choices of P1 and P2 the curve may intersect itself, or contain a cusp.
Recursive definition
A recursive definition for the Bézier curve of degree n expresses it as a linear interpolationLinear interpolation
Linear interpolation is a method of curve fitting using linear polynomials. Lerp is an abbreviation for linear interpolation, which can also be used as a verb .-Linear interpolation between two known points:...
between two Bézier curves of degree n − 1.
Let
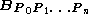 denote the Bézier curve determined by the points P0, P1, ..., Pn. Then
denote the Bézier curve determined by the points P0, P1, ..., Pn. Then to start, and
to start, and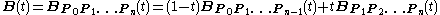
This recursion is elucidated in the animations below.
Explicit definition
The formula can be expressed explicitly as follows: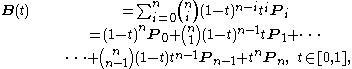
where
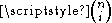 is the binomial coefficient
is the binomial coefficientBinomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
.
For example, for n = 5:
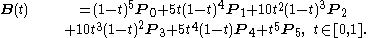
Terminology
Some terminology is associated with these parametric curves. We have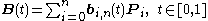
where the polynomials

are known as Bernstein basis polynomials
Bernstein polynomial
In the mathematical field of numerical analysis, a Bernstein polynomial, named after Sergei Natanovich Bernstein, is a polynomial in the Bernstein form, that is a linear combination of Bernstein basis polynomials....
of degree n, defining t0 = 1 and (1 − t)0 = 1. The binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
,
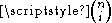 , has the alternative notation,
, has the alternative notation,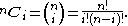
The points Pi are called control points for the Bézier curve. The polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
formed by connecting the Bézier points with lines
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
, starting with P0 and finishing with Pn, is called the Bézier polygon (or control polygon). The convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of the Bézier polygon contains the Bézier curve.
Properties
- The curve begins at P0 and ends at Pn; this is the so-called endpoint interpolation property.
- The curve is a straight line if and only if all the control points are collinear.
- The start (end) of the curve is tangentTangentIn geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
to the first (last) section of the Bézier polygon. - A curve can be split at any point into two subcurves, or into arbitrarily many subcurves, each of which is also a Bézier curve.
- Some curves that seem simple, such as the circleCircleA circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
, cannot be described exactly by a Bézier or piecewisePiecewiseOn mathematics, a piecewise-defined function is a function whose definition changes depending on the value of the independent variable...
Bézier curve; though a four-piece cubic Bézier curve can approximate a circle (see Bézier splineBézier splineIn the mathematical field of numerical analysis and in computer graphics, a Bézier spline is a spline curve where each polynomial of the spline is in Bézier form....
), with a maximum radial error of less than one part in a thousand, when each inner control point (or offline point) is the distance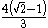 horizontally or vertically from an outer control point on a unit circle. More generally, an n-piece cubic Bézier curve can approximate a circle, when each inner control point is the distance
horizontally or vertically from an outer control point on a unit circle. More generally, an n-piece cubic Bézier curve can approximate a circle, when each inner control point is the distance 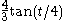 from an outer control point on a unit circle, where t is 360/n degrees, and n > 2.
from an outer control point on a unit circle, where t is 360/n degrees, and n > 2. - The curve at a fixed offset from a given Bézier curve, often called an offset curve (lying "parallel" to the original curve, like the offset between rails in a railroad track), cannot be exactly formed by a Bézier curve (except in some trivial cases). However, there are heuristicHeuristicHeuristic refers to experience-based techniques for problem solving, learning, and discovery. Heuristic methods are used to speed up the process of finding a satisfactory solution, where an exhaustive search is impractical...
methods that usually give an adequate approximation for practical purposes. - Every quadratic Bézier curve is also a cubic Bézier curve, and more generally, every degree n Bézier curve is also a degree m curve for any m > n. In detail, a degree n curve with control points P0, …, Pn is equivalent (including the parametrization) to the degree n + 1 curve with control points P'0, …, P'n + 1, where
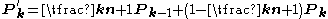 .
.
Linear curves
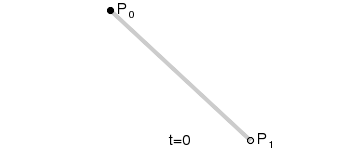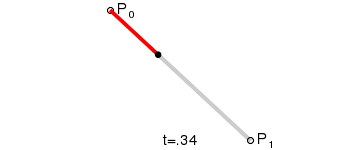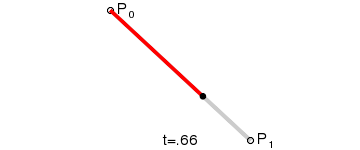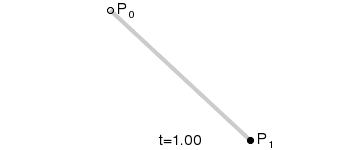 |
| Animation of a linear Bézier curve, t in [0,1] |
The t in the function for a linear Bézier curve can be thought of as describing how far B(t) is from P0 to P1. For example when t=0.25, B(t) is one quarter of the way from point P0 to P1. As t varies from 0 to 1, B(t) describes a straight line from P0 to P1.
Quadratic curves
For quadratic Bézier curves one can construct intermediate points Q0 and Q1 such that as t varies from 0 to 1:- Point Q0 varies from P0 to P1 and describes a linear Bézier curve.
- Point Q1 varies from P1 to P2 and describes a linear Bézier curve.
- Point B(t) varies from Q0 to Q1 and describes a quadratic Bézier curve.
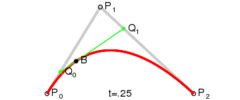 |
 |
|
| Construction of a quadratic Bézier curve | Animation of a quadratic Bézier curve, t in [0,1] |
Higher-order curves
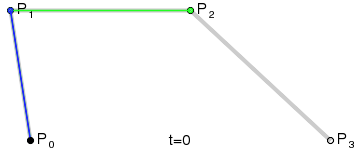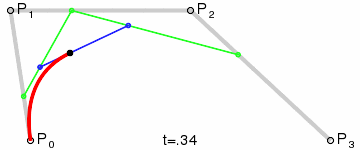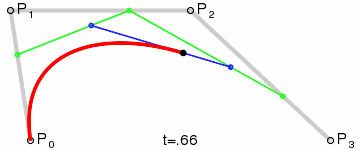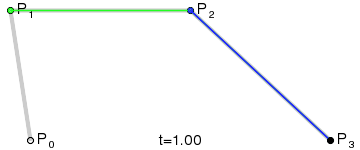
For higher-order curves one needs correspondingly more intermediate points. For cubic curves one can construct intermediate points Q0, Q1, and Q2 that describe linear Bézier curves, and points R0 & R1 that describe quadratic Bézier curves: |
 |
|
| Construction of a cubic Bézier curve | Animation of a cubic Bézier curve, t in [0,1] |
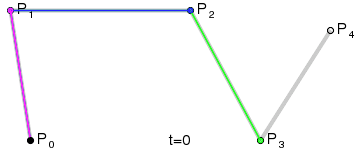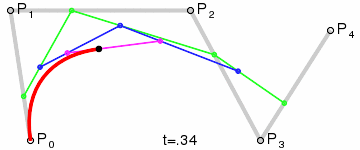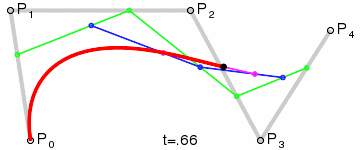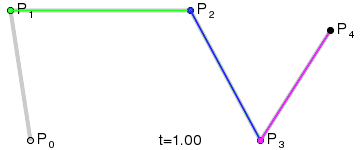
For fourth-order curves one can construct intermediate points Q0, Q1, Q2 & Q3 that describe linear Bézier curves, points R0, R1 & R2 that describe quadratic Bézier curves, and points S0 & S1 that describe cubic Bézier curves:
 |
 |
|
| Construction of a quartic Bézier curve | Animation of a quartic Bézier curve, t in [0,1] |
For fifth-order curves, one can construct similar intermediate points.
| Animation of a fifth order Bézier curve, t in [0,1] |
Degree elevation
A Bézier curve of degree n can be converted into a Bézier curve of degree n + 1 with the same shape. This is useful if software supports Bézier curves only of specific degree. For example, you can draw a quadratic Bézier curve with CairoCairo (graphics)
cairo is a software library used to provide a vector graphics-based, device-independent API for software developers. It is designed to provide primitives for 2-dimensional drawing across a number of different backends...
, which supports only cubic Bézier curves.
To do degree elevation, we use the equality
 . Each component
. Each component 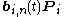 is multiplied by (1 − t) or t, thus increasing a degree by one. Here is the example of increasing degree from 2 to 3.
is multiplied by (1 − t) or t, thus increasing a degree by one. Here is the example of increasing degree from 2 to 3.-
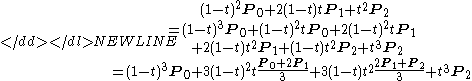
For arbitrary n we use equalities
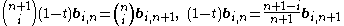
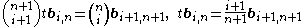
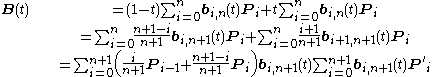
introducing arbitrary and
and 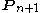 .
.
Therefore new control points are
Polynomial form
Sometimes it is desirable to express the Bézier curve as a polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
instead of a sum of less straightforward Bernstein polynomialBernstein polynomialIn the mathematical field of numerical analysis, a Bernstein polynomial, named after Sergei Natanovich Bernstein, is a polynomial in the Bernstein form, that is a linear combination of Bernstein basis polynomials....
s. Application of the binomial theoremBinomial theoremIn elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
to the definition of the curve followed by some rearrangement will yield:
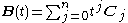
where
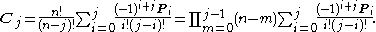
This could be practical if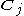 can be computed prior to many evaluations of
can be computed prior to many evaluations of 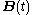 ; however one should use caution as high order curves may lack numeric stability (de Casteljau's algorithmDe Casteljau's algorithmIn the mathematical field of numerical analysis, De Casteljau's algorithm is a recursive method to evaluate polynomials in Bernstein form or Bézier curves, named after its inventor Paul de Casteljau...
; however one should use caution as high order curves may lack numeric stability (de Casteljau's algorithmDe Casteljau's algorithmIn the mathematical field of numerical analysis, De Casteljau's algorithm is a recursive method to evaluate polynomials in Bernstein form or Bézier curves, named after its inventor Paul de Casteljau...
should be used if this occurs). Note that the empty productEmpty productIn mathematics, an empty product, or nullary product, is the result of multiplying no factors. It is equal to the multiplicative identity 1, given that it exists for the multiplication operation in question, just as the empty sum—the result of adding no numbers—is zero, or the additive...
is 1.
Rational Bézier curves
The rational Bézier curve adds adjustable weights to provide closer approximations to arbitrary shapes. The numerator is a weighted Bernstein-form Bézier curve and the denominator is a weighted sum of Bernstein polynomial Bernstein polynomialIn the mathematical field of numerical analysis, a Bernstein polynomial, named after Sergei Natanovich Bernstein, is a polynomial in the Bernstein form, that is a linear combination of Bernstein basis polynomials....
Bernstein polynomialIn the mathematical field of numerical analysis, a Bernstein polynomial, named after Sergei Natanovich Bernstein, is a polynomial in the Bernstein form, that is a linear combination of Bernstein basis polynomials....
s. Rational Bézier curves can, among other uses, be used to represent segments of conic sectionConic sectionIn mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
s exactly.
Given n + 1 control points Pi, the rational Bézier curve can be described by: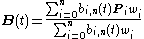
or simply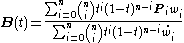
See also
- NURBS
- String artString artString art, or pin and thread art, is characterized by an arrangement of colored thread strung between points to form abstract geometric patterns or representational designs such as a ship's sails, sometimes with other artist material comprising the remainder of the work. Thread, wire, or string is...
– Bézier curves are also formed by many common forms of string art, where strings are looped across a frame of nails. - Hermite curve
External links
- Finding All Intersections of Two Bézier Curves. – Locating all the intersections between two Bézier curves is a difficult general problem, because of the variety of degenerate cases. By Richard J. Kinch.
- From Bézier to Bernstein Feature Column from American Mathematical SocietyAmerican Mathematical SocietyThe American Mathematical Society is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, which it does with various publications and conferences as well as annual monetary awards and prizes to mathematicians.The society is one of the...
-