
Hat matrix
Encyclopedia
In statistics
, the hat matrix, H, maps the vector of observed values to the vector of fitted values. It describes the influence each observed value has on each fitted value. The diagonal elements of the hat matrix are the leverage
s, which describe the influence each observed value has on the fitted value for that same observation.
If the vector of observed values is denoted by y and the vector of fitted values by ŷ,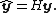
As ŷ is usually pronounced "y-hat", the hat matrix is so named as it "puts a hat
on y".
Suppose that we wish to solve a linear model
using linear least squares
. The model can be written as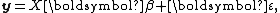
where X is a matrix of explanatory variables (the design matrix
), β is a vector of unknown parameters to be estimated, and ε is the error vector.
, the estimated parameters are
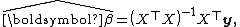
so the fitted values are
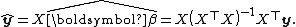
Therefore the hat matrix is given by
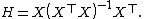
In the language of linear algebra
, the hat matrix is the orthogonal projection onto the column space
of the design matrix X. (Note that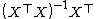 is the pseudoinverse of X.)
is the pseudoinverse of X.)
The hat matrix corresponding to a linear model
is symmetric and idempotent, that is, H2 = H. However, this is not always the case; in locally weighted scatterplot smoothing (LOESS)
, for example, the hat matrix is in general neither symmetric nor idempotent.
The formula for the vector of residual
s r can be expressed compactly using the hat matrix:
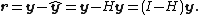
The covariance matrix
of the residuals is therefore, by error propagation, equal to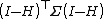 , where Σ is the covariance matrix of the errors (and by extension, the observations as well). For the case of linear models with independent and identically distributed errors in which Σ = σ2I, this reduces to (I − H)σ2.
, where Σ is the covariance matrix of the errors (and by extension, the observations as well). For the case of linear models with independent and identically distributed errors in which Σ = σ2I, this reduces to (I − H)σ2.
For linear models, the trace
of the hat matrix is equal to the rank
of X, which is the number of independent parameters of the linear model. For other models such as LOESS that are still linear in the observations y, the hat matrix can be used to define the effective degrees of freedom of the model.
The hat matrix has a number of useful algebraic properties. Practical applications of the hat matrix in regression analysis include leverage
and Cook's distance
, which are concerned with identifying observations which have a large effect on the results of a regression.
of the errors is Σ. Then since
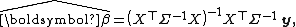
the hat matrix is thus
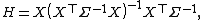
and again it may be seen that H2 = H.
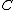 can be decomposed by columns as
can be decomposed by columns as 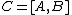 .
.
Define the Hat operator as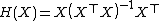 . Similarly, define the residual operator as
. Similarly, define the residual operator as 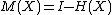 .
.
Then the Hat matrix of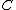 can be decomposed as follows:
can be decomposed as follows:
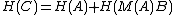
There are a number of applications of such a partitioning. The classical application has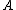 a column of all ones, which allows one to analyze the effects of adding an intercept term to a regression. Another use is in the fixed effects model, where
a column of all ones, which allows one to analyze the effects of adding an intercept term to a regression. Another use is in the fixed effects model, where 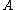 is a large sparse matrix of the dummy variables for the fixed effect terms. One can use this partition to compute the hat matrix of
is a large sparse matrix of the dummy variables for the fixed effect terms. One can use this partition to compute the hat matrix of 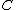 without explicitly forming the matrix
without explicitly forming the matrix 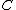 , which might be too large to fit into computer memory.
, which might be too large to fit into computer memory.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the hat matrix, H, maps the vector of observed values to the vector of fitted values. It describes the influence each observed value has on each fitted value. The diagonal elements of the hat matrix are the leverage
Leverage (statistics)
In statistics, leverage is a term used in connection with regression analysis and, in particular, in analyses aimed at identifying those observations that are far away from corresponding average predictor values...
s, which describe the influence each observed value has on the fitted value for that same observation.
If the vector of observed values is denoted by y and the vector of fitted values by ŷ,
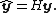
As ŷ is usually pronounced "y-hat", the hat matrix is so named as it "puts a hat
Circumflex
The circumflex is a diacritic used in the written forms of many languages, and is also commonly used in various romanization and transcription schemes. It received its English name from Latin circumflexus —a translation of the Greek περισπωμένη...
on y".
Suppose that we wish to solve a linear model
Linear model
In statistics, the term linear model is used in different ways according to the context. The most common occurrence is in connection with regression models and the term is often taken as synonymous with linear regression model. However the term is also used in time series analysis with a different...
using linear least squares
Linear least squares
In statistics and mathematics, linear least squares is an approach to fitting a mathematical or statistical model to data in cases where the idealized value provided by the model for any data point is expressed linearly in terms of the unknown parameters of the model...
. The model can be written as
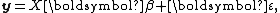
where X is a matrix of explanatory variables (the design matrix
Design matrix
In statistics, a design matrix is a matrix of explanatory variables, often denoted by X, that is used in certain statistical models, e.g., the general linear model....
), β is a vector of unknown parameters to be estimated, and ε is the error vector.
Uncorrelated errors
For uncorrelated errorsErrors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
, the estimated parameters are
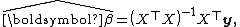
so the fitted values are
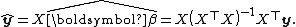
Therefore the hat matrix is given by
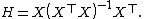
In the language of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the hat matrix is the orthogonal projection onto the column space
Column space
In linear algebra, the column space of a matrix is the set of all possible linear combinations of its column vectors. The column space of an m × n matrix is a subspace of m-dimensional Euclidean space...
of the design matrix X. (Note that
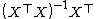 is the pseudoinverse of X.)
is the pseudoinverse of X.)The hat matrix corresponding to a linear model
Linear model
In statistics, the term linear model is used in different ways according to the context. The most common occurrence is in connection with regression models and the term is often taken as synonymous with linear regression model. However the term is also used in time series analysis with a different...
is symmetric and idempotent, that is, H2 = H. However, this is not always the case; in locally weighted scatterplot smoothing (LOESS)
Local regression
LOESS, or LOWESS , is one of many "modern" modeling methods that build on "classical" methods, such as linear and nonlinear least squares regression. Modern regression methods are designed to address situations in which the classical procedures do not perform well or cannot be effectively applied...
, for example, the hat matrix is in general neither symmetric nor idempotent.
The formula for the vector of residual
Errors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
s r can be expressed compactly using the hat matrix:
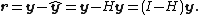
The covariance matrix
Covariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
of the residuals is therefore, by error propagation, equal to
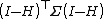 , where Σ is the covariance matrix of the errors (and by extension, the observations as well). For the case of linear models with independent and identically distributed errors in which Σ = σ2I, this reduces to (I − H)σ2.
, where Σ is the covariance matrix of the errors (and by extension, the observations as well). For the case of linear models with independent and identically distributed errors in which Σ = σ2I, this reduces to (I − H)σ2.For linear models, the trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of the hat matrix is equal to the rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
of X, which is the number of independent parameters of the linear model. For other models such as LOESS that are still linear in the observations y, the hat matrix can be used to define the effective degrees of freedom of the model.
The hat matrix has a number of useful algebraic properties. Practical applications of the hat matrix in regression analysis include leverage
Leverage (statistics)
In statistics, leverage is a term used in connection with regression analysis and, in particular, in analyses aimed at identifying those observations that are far away from corresponding average predictor values...
and Cook's distance
Cook's distance
In statistics, Cook's distance is a commonly used estimate of the influence of a data point when doing least squares regression analysis. In a practical ordinary least squares analysis, Cook's distance can be used in several ways: to indicate data points that are particularly worth checking for...
, which are concerned with identifying observations which have a large effect on the results of a regression.
Correlated errors
The above may be generalized to the case of correlated errors. Suppose that the covariance matrixCovariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
of the errors is Σ. Then since
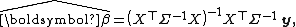
the hat matrix is thus
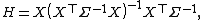
and again it may be seen that H2 = H.
Blockwise formula
Suppose the design matrix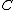 can be decomposed by columns as
can be decomposed by columns as 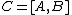 .
.Define the Hat operator as
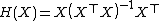 . Similarly, define the residual operator as
. Similarly, define the residual operator as 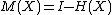 .
.Then the Hat matrix of
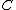 can be decomposed as follows:
can be decomposed as follows: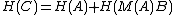
There are a number of applications of such a partitioning. The classical application has
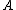 a column of all ones, which allows one to analyze the effects of adding an intercept term to a regression. Another use is in the fixed effects model, where
a column of all ones, which allows one to analyze the effects of adding an intercept term to a regression. Another use is in the fixed effects model, where 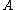 is a large sparse matrix of the dummy variables for the fixed effect terms. One can use this partition to compute the hat matrix of
is a large sparse matrix of the dummy variables for the fixed effect terms. One can use this partition to compute the hat matrix of 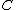 without explicitly forming the matrix
without explicitly forming the matrix 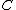 , which might be too large to fit into computer memory.
, which might be too large to fit into computer memory.See also
- Moore–Penrose pseudoinverse
- Studentized residuals
- Effective degrees of freedom

