
Frobenius matrix
Encyclopedia
A Frobenius matrix is a special kind of square matrix from the branch of mathematics known as numerical mathematics. A matrix is a Frobenius matrix if it has the following three properties:
The following matrix is an example.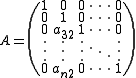
Frobenius matrices are invertible. The inverse of a Frobenius matrix is again a Frobenius matrix. It is equal to the original matrix with changed signs outside the main diagonal. The inverse of the example above is therefore:
Frobenius matrices are named after Ferdinand Georg Frobenius
. An alternative name for this class of matrices is Gauss transformation, after Carl Friedrich Gauss
. They are used in the process of Gaussian elimination
to represent the Gaussian transformations.
If a matrix is multiplied from the left (left multiplied) with a Frobenius matrix, a linear combination
of
the remaining rows is added to a particular row of the matrix. Multiplication with the inverse matrix subtracts the corresponding linear combination from the given row. This corresponds to one of the elementary operations of Gaussian elimination (besides the operation of transposing the rows and multiplying a row with a scalar multiple).
- all entries on the main diagonal are ones
- the entries below the main diagonal of at most one column are arbitrary
- every other entry is zero
The following matrix is an example.

Frobenius matrices are invertible. The inverse of a Frobenius matrix is again a Frobenius matrix. It is equal to the original matrix with changed signs outside the main diagonal. The inverse of the example above is therefore:

Frobenius matrices are named after Ferdinand Georg Frobenius
Ferdinand Georg Frobenius
Ferdinand Georg Frobenius was a German mathematician, best known for his contributions to the theory of differential equations and to group theory...
. An alternative name for this class of matrices is Gauss transformation, after Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
. They are used in the process of Gaussian elimination
Gaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
to represent the Gaussian transformations.
If a matrix is multiplied from the left (left multiplied) with a Frobenius matrix, a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of
the remaining rows is added to a particular row of the matrix. Multiplication with the inverse matrix subtracts the corresponding linear combination from the given row. This corresponds to one of the elementary operations of Gaussian elimination (besides the operation of transposing the rows and multiplying a row with a scalar multiple).

