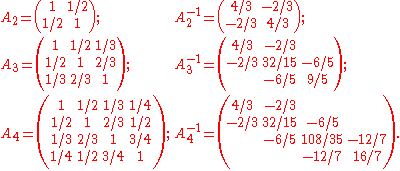Lehmer matrix
Encyclopedia
In mathematics
, particularly matrix theory, the n×n Lehmer matrix (named after Derrick Henry Lehmer
) is the constant symmetric matrix defined by
Alternatively, this may be written as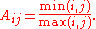
Interestingly, the inverse of a Lehmer matrix is a tridiagonal matrix, where the superdiagonal and subdiagonal have strictly negative entries. Consider again the n×n A and m×m B Lehmer matrices, where m>n. A rather peculiar property of their inverses is that A-1 is nearly a submatrix of B-1, except for the An,n element, which is not equal to Bm,m.
Clearly a Lehmer matrix of order n has trace n.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly matrix theory, the n×n Lehmer matrix (named after Derrick Henry Lehmer
Derrick Henry Lehmer
Derrick Henry "Dick" Lehmer was an American mathematician who refined Édouard Lucas' work in the 1930s and devised the Lucas–Lehmer test for Mersenne primes...
) is the constant symmetric matrix defined by

Alternatively, this may be written as
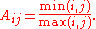
Properties
As can be seen in the examples section, if A is an n×n Lehmer matrix and B is an m×m Lehmer matrix, then A is a submatrix of B whenever m>n. The values of elements diminish toward zero away from the diagonal, where all elements have value 1.Interestingly, the inverse of a Lehmer matrix is a tridiagonal matrix, where the superdiagonal and subdiagonal have strictly negative entries. Consider again the n×n A and m×m B Lehmer matrices, where m>n. A rather peculiar property of their inverses is that A-1 is nearly a submatrix of B-1, except for the An,n element, which is not equal to Bm,m.
Clearly a Lehmer matrix of order n has trace n.
Examples
The 2×2, 3×3 and 4×4 Lehmer matrices and their inverses are shown below.