Sparse matrix - AbsoluteAstronomy.com

Numerical analysis

Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....

, a sparse matrix is a matrix

Matrix (mathematics)

In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...

populated primarily with zeros . The term itself was coined by Harry M. Markowitz.

Conceptually, sparsity corresponds to systems which are loosely coupled. Consider a line of balls connected by springs from one to the next; this is a sparse system. By contrast, if the same line of balls had springs connecting each ball to all other balls, the system would be represented by a dense matrix. The concept of sparsity is useful in combinatorics

Combinatorics

Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...

and application areas such as network theory

Network theory

Network theory is an area of computer science and network science and part of graph theory. It has application in many disciplines including statistical physics, particle physics, computer science, biology, economics, operations research, and sociology...

, which have a low density of significant data or connections.

Huge sparse matrices often appear in science

Science

Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...

or engineering

Engineering

Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...

when solving partial differential equation

Partial differential equation

In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...

s.

When storing and manipulating sparse matrices on a computer

Computer

A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...

, it is beneficial and often necessary to use specialized algorithm

Algorithm

In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...

s and data structure

Data structure

In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...

s that take advantage of the sparse structure of the matrix. Operations using standard dense matrix structures and algorithms are slow and consume large amounts of memory

Computer memory

In computing, memory refers to the physical devices used to store programs or data on a temporary or permanent basis for use in a computer or other digital electronic device. The term primary memory is used for the information in physical systems which are fast In computing, memory refers to the...

when applied to large sparse matrices. Sparse data is by nature easily compressed

Data compression

In computer science and information theory, data compression, source coding or bit-rate reduction is the process of encoding information using fewer bits than the original representation would use....

, and this compression almost always results in significantly less computer data storage usage. Indeed, some very large sparse matrices are infeasible to manipulate with the standard dense algorithms.

Storing a sparse matrix

The native data structure for a matrix is a two-dimensional array. Each entry in the array represents an element a_i,j of the matrix and can be accessed by the two indices

Index (information technology)

In computer science, an index can be:# an integer that identifies an array element# a data structure that enables sublinear-time lookup -Array element identifier:...

i and j. For an m×n matrix, enough memory to store at least (m×n) entries to represent the matrix is needed.

Substantial memory requirement reductions can be realized by storing only the non-zero entries. Depending on the number and distribution of the non-zero entries, different data structures can be used and yield huge savings in memory

Computer storage

Computer data storage, often called storage or memory, refers to computer components and recording media that retain digital data. Data storage is one of the core functions and fundamental components of computers....

when compared to a native approach.

Formats can be divided into two groups: (1) those that support efficient modification, and (2) those that support efficient matrix operations. The efficient modification group includes DOK, LIL, and COO and is typically used to construct the matrix. Once the matrix is constructed, it is typically converted to a format, such as CSR or CSC, which is more efficient for matrix operations.

Dictionary of keys (DOK)

DOK represents non-zero values as a dictionary mapping (row, column)-tuple

Tuple

In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...

s to values. This format is good for incrementally constructing a sparse array, but poor for iterating over non-zero values in sorted order. One typically creates the matrix with this format, then converts to another format for processing

List of lists (LIL)

LIL stores one list per row, where each entry stores a column index and value. Typically, these entries are kept sorted by column index for faster lookup. This is another format which is good for incremental matrix construction. See scipy.sparse.lil_matrix.

Coordinate list (COO)

COO stores a list of (row, column, value) tuples. Ideally, the entries are sorted (by row index, then column index) to improve random access times. This is another format which is good for incremental matrix construction. See scipy.sparse.coo_matrix.

Yale format

The Yale Sparse Matrix Format stores an initial sparse m×n matrix, M, in row form using three one-dimensional arrays. Let NNZ denote the number of nonzero entries of M. The first array is A, which is of length NNZ, and holds all nonzero entries of M in left-to-right top-to-bottom (row-major) order. The second array is IA, which is of length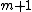

(i.e., one entry per row, plus one). IA(i) contains the index in A of the first nonzero element of row i. Row i of the original matrix extends from A(IA(i)) to A(IA(i+1)-1), i.e. from the start of one row to the last index before the start of the next. The third array, JA, contains the column index of each element of A, so it also is of length NNZ.

For example, the matrix

[ 1 2 0 0 ]
[ 0 3 9 0 ]
[ 0 1 4 0 ]

is a three-by-four matrix with six nonzero elements, so
A = [ 1 2 3 9 1 4 ]
IA = [ 0 2 4 6 ]
JA = [ 0 1 1 2 1 2 ]

In this case the Yale representation contains 16 entries, compared to only 12 in the original matrix. The Yale format saves on memory only when

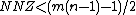Compressed sparse row (CSR or CRS)

CSR is effectively identical to the Yale Sparse Matrix format, except that the column array is normally stored ahead of the row index array. I.e. CSR is (val, col_ind, row_ptr), where val is an array of the (left-to-right, then top-to-bottom) non-zero values of the matrix; col_ind is the column indices corresponding to the values; and, row_ptr is the list of value indexes where each row starts. The name is based on the fact that row index information is compressed relative to the COO format. One typically uses another format (LIL, DOK, COO) for construction. This format is efficient for arithmetic operations, row slicing, and matrix-vector products. See scipy.sparse.csr_matrix.

Compressed sparse column (CSC or CCS)

CSC is similar to CSR except that values are read first by column, a row index is stored for each value, and column pointers are stored. I.e. CSC is (val, row_ind, col_ptr), where val is an array of the (top-to-bottom, then left-to-right-bottom) non-zero values of the matrix; row_ind is the row indices corresponding to the values; and, col_ptr is the list of val indexes where each column starts. The name is based on the fact that column index information is compressed relative to the COO format. One typically uses another format (LIL, DOK, COO) for construction. This format is efficient for arithmetic operations, column slicing, and matrix-vector products. See scipy.sparse.csc_matrix.
This is the traditional format for specifying a sparse matrix in MATLAB (via the sparse function).

Example

A bitmap

Bitmap

In computer graphics, a bitmap or pixmap is a type of memory organization or image file format used to store digital images. The term bitmap comes from the computer programming terminology, meaning just a map of bits, a spatially mapped array of bits. Now, along with pixmap, it commonly refers to...

image having only 2 colors, with one of them dominant (say a file that stores a handwritten signature

Signature

A signature is a handwritten depiction of someone's name, nickname, or even a simple "X" that a person writes on documents as a proof of identity and intent. The writer of a signature is a signatory. Similar to a handwritten signature, a signature work describes the work as readily identifying...

) can be encoded as a sparse matrix that contains only row and column numbers for pixels with the non-dominant color.

Band matrix

An important special type of sparse matrices is band matrix

Band matrix

In mathematics, particularly matrix theory, a band matrix is a sparse matrix whose non-zero entries are confined to a diagonal band, comprising the main diagonal and zero or more diagonals on either side.-Matrix bandwidth:...

, defined as follows. The lower bandwidth of a matrix A is the smallest number p such that the entry a_ij vanishes whenever i > j + p. Similarly, the upper bandwidth is the smallest p such that a_ij = 0 whenever i < j − p . For example, a tridiagonal matrix has lower bandwidth 1 and upper bandwidth 1. As another example, the following sparse matrix has lower and upper bandwidth both equal to 3. Notice that zeros are represented with dots.

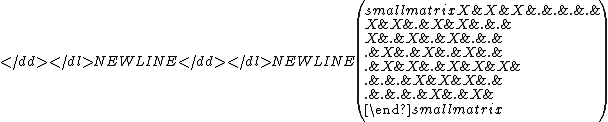
Matrices with reasonably small upper and lower bandwidth are known as band matrices and often lend themselves to simpler algorithms than general sparse matrices; or one can sometimes apply dense matrix algorithms and gain efficiency simply by looping over a reduced number of indices.

By rearranging the rows and columns of a matrix A it may be possible to obtain a matrix A’ with a lower bandwidth. A number of algorithms are designed for bandwidth minimization

Graph bandwidth

In graph theory, the graph bandwidth problem to label the n vertices vi of a graph G with distinct integers f so that the quantity \max...

Diagonal matrix

A very efficient structure for an extreme case of band matrices, the diagonal matrix

Diagonal matrix

In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...

, is to store just the entries in the main diagonal as a one-dimensional array, so a diagonal n×n matrix requires only n entries.

Reducing fill-in

"Fill-in" redirects here. For the puzzle, see Fill-In (puzzle)
Fill-In (puzzle)
Fill-Ins, also known as Fill-It-Ins or Word Fills, are a variation of the common crossword puzzle in which words, rather than clues, are given. Fill-Ins are common in puzzle magazines along with word searches, cryptograms, and other logic puzzles. Some consider Fill-Ins to be an easier version of...

.

The fill-in of a matrix are those entries which change from an initial zero to a non-zero value during the execution of an algorithm. To reduce the memory requirements and the number of arithmetic operations used during an algorithm it is useful to minimize the fill-in by switching rows and columns in the matrix. The symbolic Cholesky decomposition

Symbolic Cholesky decomposition

In the mathematical subfield of numerical analysis the symbolic Cholesky decomposition is an algorithm used to determine the non-zero pattern for the L factors of a symmetric sparse matrix when applying the Cholesky decomposition or variants.-Algorithm:...

can be used to calculate the worst possible fill-in before doing the actual Cholesky decomposition

Cholesky decomposition

In linear algebra, the Cholesky decomposition or Cholesky triangle is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose. It was discovered by André-Louis Cholesky for real matrices...

.

There are other methods than the Cholesky decomposition

Cholesky decomposition

in use. Orthogonalization methods (such as QR factorization) are common, for example, when solving problems by least squares methods. While the theoretical fill-in is still the same, in practical terms the "false non-zeros" can be different for different methods. And symbolic versions of those algorithms can be used in the same manner as the symbolic Cholesky to compute worst case fill-in.

Solving sparse matrix equations

Both iterative

Iterative method

In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...

and direct methods exist for sparse matrix solving.

Iterative methods, such as conjugate gradient method and GMRES utilize fast computations of matrix-vector products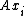

, where matrix

is sparse. The use of preconditioners

Preconditioner

In mathematics, preconditioning is a procedure of an application of a transformation, called the preconditioner, that conditions a given problem into a form that is more suitable for numerical solution. Preconditioning is typically related to reducing a condition number of the problem...

can significantly accelerate convergence of such iterative methods.

External links

Equations Solver Online
Oral history interview with Harry M. Markowitz, Charles Babbage Institute
Charles Babbage Institute
The Charles Babbage Institute is a research center at the University of Minnesota specializing in the history of information technology, particularly the history since 1935 of digital computing, programming/software, and computer networking....

, University of Minnesota. Markowitz
Harry Markowitz
Harry Max Markowitz is an American economist and a recipient of the John von Neumann Theory Prize and the Nobel Memorial Prize in Economic Sciences....

discusses his development of portfolio theory (for which he received a Nobel Prize in Economics), sparse matrix methods, and his work at the RAND Corporation and elsewhere on simulation software development (including computer language SIMSCRIPT
SIMSCRIPT
SIMSCRIPT is a free-form, English-like general-purpose simulation language conceived by Harry Markowitz and Bernard Hausner at the RAND Corporation in 1963. It was implemented as a Fortran preprocessor on the IBM 7090 and was designed for large discrete event simulations...

), modeling, and operations research.

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

Storing a sparse matrix

Dictionary of keys (DOK)

List of lists (LIL)

Coordinate list (COO)

Yale format

Compressed sparse row (CSR or CRS)

Compressed sparse column (CSC or CCS)

Example

Band matrix

Diagonal matrix

Reducing fill-in

Solving sparse matrix equations

See also

Further reading

External links