Generalized permutation matrix
Encyclopedia
In mathematics
, a generalized permutation matrix (or monomial matrix) is a matrix
with the same nonzero pattern as a permutation matrix
, i.e. there is exactly one nonzero entry in each row and each column. Unlike a permutation matrix, where the nonzero entry must be 1, in a generalized permutation matrix the nonzero entry can be any nonzero value. An example of a generalized permutation matrix is
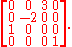
D and an (implicitly invertible) permutation matrix
P: i.e.,
F forms a subgroup
of the general linear group
GL(n,F), in which the group of nonsingular diagonal matrices Δ(n, F) forms a normal subgroup
. Indeed, the generalized permutation matrices are the normalizer of the diagonal matrices, meaning that the generalized permutation matrices are the largest subgroup of GL in which diagonal matrices are normal.
The abstract group of generalized permutation matrices is the wreath product
of F× and Sn. Concretely, this means that it is the semidirect product
of Δ(n, F) by the symmetric group
Sn:
where Sn acts by permuting coordinates and the diagonal matrices Δ(n, F) are isomorphic to the n-fold product (F×)n.
To be precise, the generalized permutation matrices are a (faithful) linear representation of this abstract wreath product: a realization of the abstract group as a subgroup of matrices.
in the ring (invertible), one again obtains a group. On the other hand, if the non-zero entries are only required to be non-zero, but not necessarily invertible, this set of matrices forms a semigroup
instead.
One may also schematically allow the non-zero entries to lie in a group G, with the understanding that matrix multiplication will only involve multiplying a single pair of group elements, not "adding" group elements. This is an abuse of notation
, since element of matrices being multiplied must allow multiplication and addition, but is suggestive notion for the (formally correct) abstract group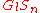
(the wreath product of the group G by the symmetric group).
in the context of monomial representation
s. A monomial representation of a group G is a linear representation ρ : G → GL(n, F) of G (here F is the defining field of the representation) such that the image ρ(G) is a subgroup of the group of monomial matrices.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a generalized permutation matrix (or monomial matrix) is a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with the same nonzero pattern as a permutation matrix
Permutation matrix
In mathematics, in matrix theory, a permutation matrix is a square binary matrix that has exactly one entry 1 in each row and each column and 0s elsewhere...
, i.e. there is exactly one nonzero entry in each row and each column. Unlike a permutation matrix, where the nonzero entry must be 1, in a generalized permutation matrix the nonzero entry can be any nonzero value. An example of a generalized permutation matrix is
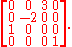
Structure
An invertible matrix A is a generalized permutation matrix if and only if it can be written as a product of an invertible diagonal matrixDiagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
D and an (implicitly invertible) permutation matrix
Permutation matrix
In mathematics, in matrix theory, a permutation matrix is a square binary matrix that has exactly one entry 1 in each row and each column and 0s elsewhere...
P: i.e.,
Group structure
The set of n×n generalized permutation matrices with entries in a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F forms a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
GL(n,F), in which the group of nonsingular diagonal matrices Δ(n, F) forms a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
. Indeed, the generalized permutation matrices are the normalizer of the diagonal matrices, meaning that the generalized permutation matrices are the largest subgroup of GL in which diagonal matrices are normal.
The abstract group of generalized permutation matrices is the wreath product
Wreath product
In mathematics, the wreath product of group theory is a specialized product of two groups, based on a semidirect product. Wreath products are an important tool in the classification of permutation groups and also provide a way of constructing interesting examples of groups.Given two groups A and H...
of F× and Sn. Concretely, this means that it is the semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of Δ(n, F) by the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Sn:
- Δ(n, F) Sn,
where Sn acts by permuting coordinates and the diagonal matrices Δ(n, F) are isomorphic to the n-fold product (F×)n.
To be precise, the generalized permutation matrices are a (faithful) linear representation of this abstract wreath product: a realization of the abstract group as a subgroup of matrices.
Subgroups
- The subgroup where all entries are 1 is exactly the permutation matrices, which is isomorphic to the symmetric group.
- The subgroup where all entries are ±1 is the signed permutation matrices, which is the hyperoctahedral groupHyperoctahedral groupIn mathematics, a hyperoctahedral group is an important type of group that can be realized as the group of symmetries of a hypercube or of a cross-polytope. Groups of this type are identified by a parameter n, the dimension of the hypercube....
. - The subgroup where the entries are mth roots of unity
is isomorphic to a generalized symmetric groupGeneralized symmetric groupIn mathematics, the generalized symmetric group is the wreath product S := Z_m \wr S_n of the cyclic group of order m and the symmetric group on n letters.- Examples :...
. - The subgroup of diagonal matrices is abelian, normal, and a maximal abelian subgroup. The quotient group is the symmetric group, and this construction is in fact the Weyl groupWeyl groupIn mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
of the general linear group: the diagonal matrices are a maximal torusMaximal torusIn the mathematical theory of compact Lie groups a special role is played by torus subgroups, in particular by the maximal torus subgroups.A torus in a Lie group G is a compact, connected, abelian Lie subgroup of G . A maximal torus is one which is maximal among such subgroups...
in the general linear group (and are their own centralizer), the generalized permutation matrices are the normalizer of this torus, and the quotient,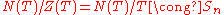
is the Weyl group.
Properties
- If a nonsingular matrix and its inverse are both nonnegative matrices (i.e. matrices with nonnegative entries), then the matrix is a generalized permutation matrix.
Generalizations
One can generalize further by allowing the entries to lie in a ring, rather than in a field. In that case if the non-zero entries are required to be unitsUnit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
in the ring (invertible), one again obtains a group. On the other hand, if the non-zero entries are only required to be non-zero, but not necessarily invertible, this set of matrices forms a semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
instead.
One may also schematically allow the non-zero entries to lie in a group G, with the understanding that matrix multiplication will only involve multiplying a single pair of group elements, not "adding" group elements. This is an abuse of notation
Abuse of notation
In mathematics, abuse of notation occurs when an author uses a mathematical notation in a way that is not formally correct but that seems likely to simplify the exposition or suggest the correct intuition . Abuse of notation should be contrasted with misuse of notation, which should be avoided...
, since element of matrices being multiplied must allow multiplication and addition, but is suggestive notion for the (formally correct) abstract group
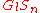(the wreath product of the group G by the symmetric group).Signed permutation group
A signed permutation matrix is a generalized permutation matrix whose nonzero entries are ±1, and are the integer generalized permutation matrices with integer inverse.Properties
- It is the Coxeter groupCoxeter groupIn mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
, and has order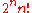 
. - It is the symmetry group of the hypercubeHypercubeIn geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
and (dually) of the cross-polytopeCross-polytopeIn geometry, a cross-polytope, orthoplex, hyperoctahedron, or cocube is a regular, convex polytope that exists in any number of dimensions. The vertices of a cross-polytope are all the permutations of . The cross-polytope is the convex hull of its vertices...
. - Its index 2 subgroup of matrices with determinant 1 is the Coxeter group
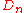and is the symmetry group of the demihypercube. - It is a subgroup of the orthogonal groupOrthogonal groupIn mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
.
Monomial representations
Monomial matrices occur in representation theoryRepresentation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
in the context of monomial representation
Monomial representation
In mathematics, a linear representation ρ of a group G is a monomial representation if there is a finite-index subgroup H and a one-dimensional linear representation σ of H, such that ρ is equivalent to the induced representation...
s. A monomial representation of a group G is a linear representation ρ : G → GL(n, F) of G (here F is the defining field of the representation) such that the image ρ(G) is a subgroup of the group of monomial matrices.