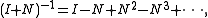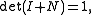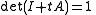Nilpotent matrix
Encyclopedia
In linear algebra
, a nilpotent matrix is a square matrix N such that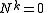
for some positive integer
k. The smallest such k is sometimes called the degree of N.
More generally, a nilpotent transformation is a linear transformation
L of a vector space
such that Lk = 0 for some positive integer k. Both of these concepts are special cases of a more general concept of nilpotence
that applies to elements of rings.
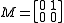
is nilpotent, since M2 = 0. More generally, any triangular matrix
with 0s along the main diagonal is nilpotent. For example, the matrix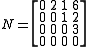
is nilpotent, with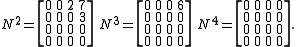
Though the examples above have a large number of zero entries, a typical nilpotent matrix does not. For example, the matrices
both square to zero, though neither matrix has zero entries.
(or complex
) entries, the following are equivalent:
The same theorem holds true for matrices over any field
.
This theorem has several consequences, including:
:
This matrix has 1s along the superdiagonal and 0s everywhere else. As a linear transformation, the shift matrix “shifts” the components of a vector one slot to the left: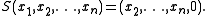
This matrix is nilpotent with degree n, and is the “canonical” nilpotent matrix.
Specifically, if N is any nilpotent matrix, then N is similar to a block diagonal matrix of the form
where each of the blocks S1, S2, ..., Sr is a shift matrix (possibly of different sizes). This theorem is a special case of the Jordan canonical form for matrices.
For example, any nonzero 2 × 2 nilpotent matrix is similar to the matrix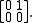
That is, if N is any nonzero 2 × 2 nilpotent matrix, then there exists a basis b1, b2 such that Nb1 = 0 and Nb2 = b1.
This classification theorem holds for matrices over any field
. (It is not necessary for the field to be algebraically closed.)
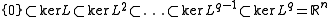
and a signature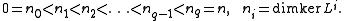
The signature characterizes L up to
an invertible linear transformation
. Furthermore, it satisfies the inequalities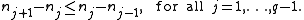
Conversely, any sequence of natural numbers satisfying these inequalities is the signature of a nilpotent transformation.
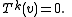
For operators on a finite-dimensional vector space, local nilpotence is equivalent to nilpotence.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a nilpotent matrix is a square matrix N such that
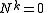
for some positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
k. The smallest such k is sometimes called the degree of N.
More generally, a nilpotent transformation is a linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
L of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
such that Lk = 0 for some positive integer k. Both of these concepts are special cases of a more general concept of nilpotence
Nilpotent
In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
that applies to elements of rings.
Examples
The matrix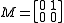
is nilpotent, since M2 = 0. More generally, any triangular matrix
Triangular matrix
In the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
with 0s along the main diagonal is nilpotent. For example, the matrix
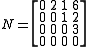
is nilpotent, with
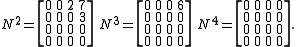
Though the examples above have a large number of zero entries, a typical nilpotent matrix does not. For example, the matrices

both square to zero, though neither matrix has zero entries.
Characterization
For an n × n square matrix N with realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
(or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
) entries, the following are equivalent:
- N is nilpotent.
- The minimal polynomialMinimal polynomial (linear algebra)In linear algebra, the minimal polynomial of an n-by-n matrix A over a field F is the monic polynomial P over F of least degree such that P=0...
for N is λk for some positive integer k ≤ n. - The characteristic polynomialCharacteristic polynomialIn linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
for N is λn. - The only (complex) eigenvalue for N is 0.
- trTrace (linear algebra)In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
(Nk) = 0 for all k > 0.
The same theorem holds true for matrices over any field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
.
This theorem has several consequences, including:
- The degree of an n × n nilpotent matrix is always less than or equal to n. For example, every 2 × 2 nilpotent matrix squares to zero.
- The determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
and traceTrace (linear algebra)In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of a nilpotent matrix are always zero. - The only nilpotent diagonalizable matrixDiagonalizable matrixIn linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
is the zero matrix.
Classification
Consider the n × n shift matrixShift matrix
In mathematics, a shift matrix is a binary matrix with ones only on the superdiagonal or subdiagonal, and zeroes elsewhere. A shift matrix U with ones on the superdiagonal is an upper shift matrix....
:

This matrix has 1s along the superdiagonal and 0s everywhere else. As a linear transformation, the shift matrix “shifts” the components of a vector one slot to the left:
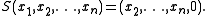
This matrix is nilpotent with degree n, and is the “canonical” nilpotent matrix.
Specifically, if N is any nilpotent matrix, then N is similar to a block diagonal matrix of the form

where each of the blocks S1, S2, ..., Sr is a shift matrix (possibly of different sizes). This theorem is a special case of the Jordan canonical form for matrices.
For example, any nonzero 2 × 2 nilpotent matrix is similar to the matrix
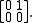
That is, if N is any nonzero 2 × 2 nilpotent matrix, then there exists a basis b1, b2 such that Nb1 = 0 and Nb2 = b1.
This classification theorem holds for matrices over any field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
. (It is not necessary for the field to be algebraically closed.)
Flag of subspaces
A nilpotent transformation L on Rn naturally determines a flag of subspaces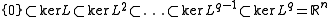
and a signature
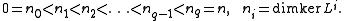
The signature characterizes L up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
an invertible linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
. Furthermore, it satisfies the inequalities
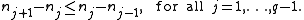
Conversely, any sequence of natural numbers satisfying these inequalities is the signature of a nilpotent transformation.
Additional properties
- If N is nilpotent, then I + N is invertible, where I is the n × n identity matrixIdentity matrixIn linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. The inverse is given by
-
- where only finitely many terms of this sum are nonzero.
- If N is nilpotent, then
-
- where I denotes the n × n identity matrix. Conversely, if A is a matrix and
- for all values of t, then A is nilpotent.
- Every singular matrix can be written as a product of nilpotent matrices.
Generalizations
A linear operator T is locally nilpotent if for every vector v, there exists a k such that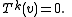
For operators on a finite-dimensional vector space, local nilpotence is equivalent to nilpotence.
External links
- Nilpotent matrix and nilpotent transformation on PlanetMathPlanetMathPlanetMath is a free, collaborative, online mathematics encyclopedia. The emphasis is on rigour, openness, pedagogy, real-time content, interlinked content, and also community of about 24,000 people with various maths interests. Intended to be comprehensive, the project is hosted by the Digital...
.