
Walsh matrix
Encyclopedia
In mathematics
, a Walsh matrix is a specific square matrix, with dimensions a power of 2, the entries of which are +1 or −1, and the property that the dot product
of any two distinct rows (or columns) is zero. The Walsh matrix was proposed by Joseph Leonard Walsh
in 1923. Each row of a Walsh matrix corresponds to a Walsh function
.
The natural ordered Hadamard matrix is defined by the recursive
formula below, and the sequency ordered Hadamard matrix is formed by rearranging the rows so that the number of sign-changes in a row is in increasing order. Confusingly, different sources refer to either matrix as the Walsh matrix.
The Walsh matrix (and Walsh function
s) are used in computing the Walsh transform and have applications in the efficient implementation of certain signal processing operations.
The lowest order of Hadamard matrix is 2
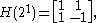
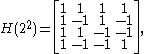
and in general
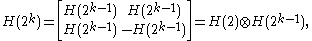
for 2 ≤ k ∈ N, where denotes the Kronecker product
denotes the Kronecker product
.
and then the Gray code
permutation
.
e.g.
where the successive rows have 0, 1, 2, and 3 sign changes.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Walsh matrix is a specific square matrix, with dimensions a power of 2, the entries of which are +1 or −1, and the property that the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of any two distinct rows (or columns) is zero. The Walsh matrix was proposed by Joseph Leonard Walsh
Joseph Leonard Walsh
Joseph Leonard Walsh, was an American mathematician. His work was mainly in the field of analysis.For most of his professional career he studied and worked at Harvard University. He received a B.S. in 1916 and a PhD in 1920. The Advisor of his PhD was Maxime Bôcher...
in 1923. Each row of a Walsh matrix corresponds to a Walsh function
Walsh function
In mathematical analysis, the set of Walsh functions form an orthogonal basis of the square-integrable functions on the unit interval. The functions take the values -1 and +1 only, on sub-intervals defined by dyadic fractions...
.
The natural ordered Hadamard matrix is defined by the recursive
Recursive
Recursive may refer to:*Recursion, the technique of functions calling themselves*Recursive function, a total computable function*Recursive language, a language which is decidable...
formula below, and the sequency ordered Hadamard matrix is formed by rearranging the rows so that the number of sign-changes in a row is in increasing order. Confusingly, different sources refer to either matrix as the Walsh matrix.
The Walsh matrix (and Walsh function
Walsh function
In mathematical analysis, the set of Walsh functions form an orthogonal basis of the square-integrable functions on the unit interval. The functions take the values -1 and +1 only, on sub-intervals defined by dyadic fractions...
s) are used in computing the Walsh transform and have applications in the efficient implementation of certain signal processing operations.
Formula
The Hadamard matrices of dimension 2k for k ∈ N are given by the recursive formulaThe lowest order of Hadamard matrix is 2
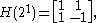
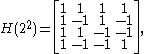
and in general
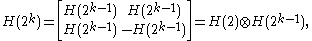
for 2 ≤ k ∈ N, where
 denotes the Kronecker product
denotes the Kronecker productKronecker product
In mathematics, the Kronecker product, denoted by ⊗, is an operation on two matrices of arbitrary size resulting in a block matrix. It gives the matrix of the tensor product with respect to a standard choice of basis. The Kronecker product should not be confused with the usual matrix...
.
Sequency ordering
The sequency ordering of the rows of the Walsh matrix can be derived from the ordering of the Hadamard matrix by first applying the bit-reversal permutationBit-reversal permutation
In applied mathematics, a bit-reversal permutation is a permutation of a sequence with n = 2m elements, defined by reversing the binary digits of the index of each element...
and then the Gray code
Gray code
The reflected binary code, also known as Gray code after Frank Gray, is a binary numeral system where two successive values differ in only one bit. It is a non-weighted code....
permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
.
e.g.

where the successive rows have 0, 1, 2, and 3 sign changes.
See also
- Haar waveletHaar waveletIn mathematics, the Haar wavelet is a certain sequence of rescaled "square-shaped" functions which together form a wavelet family or basis. Wavelet analysis is similar to Fourier analysis in that it allows a target function over an interval to be represented in terms of an orthonormal function basis...
- Quincunx matrix
- Hadamard transformHadamard transformThe Hadamard transform is an example of a generalized class of Fourier transforms...

