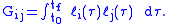Gramian matrix
Encyclopedia
In linear algebra
, the Gramian matrix (or Gram matrix or Gramian) of a set of vectors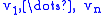 in an inner product space
in an inner product space
is the Hermitian matrix of inner products, whose entries are given by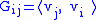 .
.
An important application is to compute linear independence
: a set of vectors is linearly independent if and only if the Gram determinant (the determinant
of the Gram matrix) is non-zero.
It is named after Jørgen Pedersen Gram
.
, or are functions
in an L2 space, such as continuous functions on a compact interval
[a, b] (which are a subspace of L 2([a, b])).
Given real
-valued functions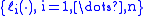 on the interval
on the interval 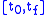 , the Gram matrix
, the Gram matrix 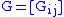 , is given by the standard inner product on functions:
, is given by the standard inner product on functions:
Given a real matrix A, the matrix ATA is a Gram matrix (of the columns of A), while the matrix AAT is the Gram matrix of the rows of A.
For a general bilinear form B on a finite-dimensional vector space
over any field
we can define a Gram matrix G attached to a set of vectors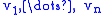 by
by 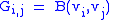 . The matrix will be symmetric if the bilinear form B is symmetric.
. The matrix will be symmetric if the bilinear form B is symmetric.
is the identity matrix.
The infinite-dimensional analog of this statement is Mercer's theorem
.
to PTGP.
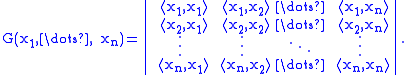
Geometrically, the Gram determinant is the square of the volume of the parallelotope formed by the vectors. In particular, the vectors are linearly independent
if and only if the Gram determinant is nonzero (if and only if the Gram matrix is nonsingular).
The Gram determinant can also be expressed in terms of the exterior product of vectors by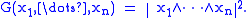
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the Gramian matrix (or Gram matrix or Gramian) of a set of vectors
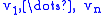 in an inner product space
in an inner product spaceInner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
is the Hermitian matrix of inner products, whose entries are given by
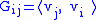 .
.An important application is to compute linear independence
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
: a set of vectors is linearly independent if and only if the Gram determinant (the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the Gram matrix) is non-zero.
It is named after Jørgen Pedersen Gram
Jørgen Pedersen Gram
Jørgen Pedersen Gram was a Danish actuary and mathematician who was born in Nustrup, Duchy of Schleswig, Denmark and died in Copenhagen, Denmark....
.
Examples
Most commonly, the vectors are elements of an Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, or are functions
in an L2 space, such as continuous functions on a compact interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[a, b] (which are a subspace of L 2([a, b])).
Given real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
-valued functions
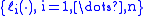 on the interval
on the interval 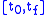 , the Gram matrix
, the Gram matrix 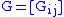 , is given by the standard inner product on functions:
, is given by the standard inner product on functions:Given a real matrix A, the matrix ATA is a Gram matrix (of the columns of A), while the matrix AAT is the Gram matrix of the rows of A.
For a general bilinear form B on a finite-dimensional vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over any field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
we can define a Gram matrix G attached to a set of vectors
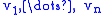 by
by 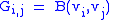 . The matrix will be symmetric if the bilinear form B is symmetric.
. The matrix will be symmetric if the bilinear form B is symmetric.Applications
- If the vectors are centered random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s, the Gramian is proportional to the covariance matrixCovariance matrixIn probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
, with the scaling determined by the number of elements in the vector. - In quantum chemistryQuantum chemistryQuantum chemistry is a branch of chemistry whose primary focus is the application of quantum mechanics in physical models and experiments of chemical systems...
, the Gram matrix of a set of basis vectors is the overlap matrixOverlap matrixThe overlap matrix is a square matrix, used in quantum chemistry to describe the inter-relationship of a set of basis vectors of a quantum system. In particular, if the vectors are orthogonal to one another, the overlap matrix will be diagonal. In addition, if the basis vectors form an...
. - In control theoryControl theoryControl theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
(or more generally systems theorySystems theorySystems theory is the transdisciplinary study of systems in general, with the goal of elucidating principles that can be applied to all types of systems at all nesting levels in all fields of research...
), the controllability Gramian and observability Gramian determine properties of a linear system. - Gramian matrices arise in covariance structure model fitting (see e.g., Jamshidian and Bentler, 1993, Applied Psychological Measurement, Volume 18, pp. 79–94).
- In the finite element methodFinite element methodThe finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
, the Gram matrix arises from approximating a function from a finite dimensional space; the Gram matrix entries are then the inner products of the basis functions of the finite dimensional subspace. - In machine learningMachine learningMachine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
, kernel functions are often represented as Gram matrices.
Positive semidefinite
The Gramian matrix is positive semidefinite, and every positive semidefinite matrix is the Gramian matrix for some set of vectors. Further, in finite-dimensions it determines the vectors up to isomorphism, i.e. any two sets of vectors with the same Gramian matrix must be related by a single unitary matrix. The Gramian matrix of any orthonormal basisOrthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
is the identity matrix.
The infinite-dimensional analog of this statement is Mercer's theorem
Mercer's theorem
In mathematics, specifically functional analysis, Mercer's theorem is a representation of a symmetric positive-definite function on a square as a sum of a convergent sequence of product functions. This theorem, presented in , is one of the most notable results of the work of James Mercer...
.
Change of basis
Under change of basis represented by an invertible matrix P, the Gram matrix will change by a matrix congruenceMatrix congruence
In mathematics, two matrices A and B over a field are called congruent if there exists an invertible matrix P over the same field such thatwhere "T" denotes the matrix transpose...
to PTGP.
Gram determinant
The Gram determinant or Gramian is the determinant of the Gram matrix: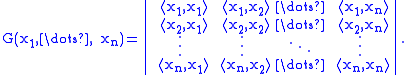
Geometrically, the Gram determinant is the square of the volume of the parallelotope formed by the vectors. In particular, the vectors are linearly independent
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
if and only if the Gram determinant is nonzero (if and only if the Gram matrix is nonsingular).
The Gram determinant can also be expressed in terms of the exterior product of vectors by
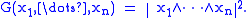
External links
- Volumes of parallelograms by Frank Jones