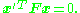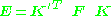Fundamental matrix (computer vision)
Encyclopedia
In computer vision
, the fundamental matrix is a 3×3 matrix
is a 3×3 matrix
which relates corresponding points in stereo image
s. In epipolar geometry
, with homogeneous image coordinates
, x and x′, of corresponding points in a stereo image pair, Fx describes a line (an epipolar line) on which the corresponding point x′ on the other image must lie. That means, for all pairs of corresponding points holds
Being of rank two and determined only up to scale, the fundamental matrix can be estimated given at least seven point correspondences. Its seven parameters represent the only geometric information about cameras that can be obtained through point correspondences alone.
The term "fundamental matrix" was coined by Luong in his influential PhD thesis. It is sometimes also referred to as the "bifocal tensor". As a tensor it is a two-point tensor
in that it is a bilinear form relating points in distinct coordinate systems.
The above relation which defines the fundamental matrix was published in 1992 by both Faugeras and Hartley. Although Longuet-Higgins' essential matrix satisfies a similar relationship, the essential matrix is a metric object pertaining to calibrated cameras, while the fundamental matrix describes the correspondence in more general and fundamental terms of projective geometry.
This is captured mathematically by the relationship between a fundamental matrix
 and its corresponding essential matrix
and its corresponding essential matrix 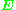 ,
,
which is
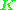 and
and 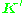 being the intrinsic calibration
being the intrinsic calibration
matrices of the two images involved.
. Additionally, these corresponding image points may be triangulated to world points with the help of camera matrices derived directly from this fundamental matrix. The scene composed of these world points is within a projective transformation of the true scene.
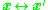 derives from the world point
derives from the world point 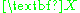 under the camera matrices
under the camera matrices 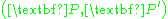 as
as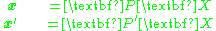 .
.
Say we transform space by a general homography
matrix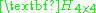 such that
such that 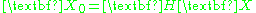 .
.
The cameras then transform as .
.
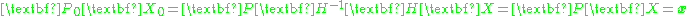 and likewise with
and likewise with 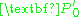 still get us the same image points.
still get us the same image points.
2. Its kernel defines the epipole.
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
, the fundamental matrix
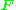 is a 3×3 matrix
is a 3×3 matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
which relates corresponding points in stereo image
Stereoscopy
Stereoscopy refers to a technique for creating or enhancing the illusion of depth in an image by presenting two offset images separately to the left and right eye of the viewer. Both of these 2-D offset images are then combined in the brain to give the perception of 3-D depth...
s. In epipolar geometry
Epipolar geometry
Epipolar geometry is the geometry of stereo vision. When two cameras view a 3D scene from two distinct positions, there are a number of geometric relations between the 3D points and their projections onto the 2D images that lead to constraints between the image points...
, with homogeneous image coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
, x and x′, of corresponding points in a stereo image pair, Fx describes a line (an epipolar line) on which the corresponding point x′ on the other image must lie. That means, for all pairs of corresponding points holds
Being of rank two and determined only up to scale, the fundamental matrix can be estimated given at least seven point correspondences. Its seven parameters represent the only geometric information about cameras that can be obtained through point correspondences alone.
The term "fundamental matrix" was coined by Luong in his influential PhD thesis. It is sometimes also referred to as the "bifocal tensor". As a tensor it is a two-point tensor
Two-point tensor
Two-point tensors, or double vectors, are tensor-like quantities which transform as vectors with respect to each of their indices and are used in continuum mechanics to transform between reference and present coordinates...
in that it is a bilinear form relating points in distinct coordinate systems.
The above relation which defines the fundamental matrix was published in 1992 by both Faugeras and Hartley. Although Longuet-Higgins' essential matrix satisfies a similar relationship, the essential matrix is a metric object pertaining to calibrated cameras, while the fundamental matrix describes the correspondence in more general and fundamental terms of projective geometry.
This is captured mathematically by the relationship between a fundamental matrix
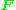 and its corresponding essential matrix
and its corresponding essential matrix 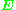 ,
,which is
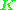 and
and 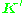 being the intrinsic calibration
being the intrinsic calibrationmatrices of the two images involved.
Introduction
The fundamental matrix is a relationship between any two images of the same scene that constrains where the projection of points from the scene can occur in both images. Given the projection of a scene point into one of the images the corresponding point in the other image is constrained to a line, helping the search, and allowing for the detection of wrong correspondences. The relation between corresponding image points which the fundamental matrix represents is referred to as epipolar constraint, matching constraint, discrete matching constraint, or incidence relation.Projective Reconstruction Theorem
The fundamental matrix can be determined by a set of point correspondencesCorrespondence problem
The correspondence problem tries to figure out which parts of an image correspond to which parts of another image, after the camera has moved, time has elapsed, and/or the objects have moved around.-Overview:...
. Additionally, these corresponding image points may be triangulated to world points with the help of camera matrices derived directly from this fundamental matrix. The scene composed of these world points is within a projective transformation of the true scene.
Proof
Say that the image point correspondence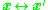 derives from the world point
derives from the world point 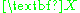 under the camera matrices
under the camera matrices 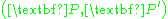 as
as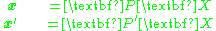 .
.Say we transform space by a general homography
Homography
Homography is a concept in the mathematical science of geometry.A homography is an invertible transformation from a projective space to itself that maps straight lines to straight lines...
matrix
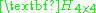 such that
such that 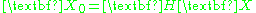 .
.The cameras then transform as
 .
.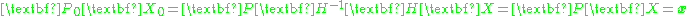 and likewise with
and likewise with 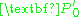 still get us the same image points.
still get us the same image points.Derivation of Fundamental matrix using coplanarity condition
Fundamental matrix can be derived using the coplanarity condition.Properties
The fundamental matrix is of rankRank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
2. Its kernel defines the epipole.
Toolboxes
- Structure and Motion Toolkit in MATLAB (Philip H. S. Torr)
- Fundamental Matrix Estimation Toolbox (Joaquim Salvi)
- The Epipolar Geometry Toolbox Toolbox (EGT)
External links
- Determining the epipolar geometry and its uncertainty: A review (Zhengyou Zhang)
- Visualization of epipolar geometry (originally by Sylvain Bougnoux of INRIA Robotvis, requires JavaJava (programming language)Java is a programming language originally developed by James Gosling at Sun Microsystems and released in 1995 as a core component of Sun Microsystems' Java platform. The language derives much of its syntax from C and C++ but has a simpler object model and fewer low-level facilities...
) - The Fundamental Matrix Song Video demonstrating laws of epipolar geometry.