Incidence matrix
Encyclopedia
In mathematics
, an incidence matrix is a matrix
that shows the relationship between two classes of objects. If the first class is X and the second is Y, the matrix has one row for each element of X and one column for each element of Y. The entry in row x and column y is 1 if x and y are related (called incident in this context) and 0 if they are not. There are variations; see below.
an undirected graph G has two kinds of incidence matrices: unoriented and oriented.
The incidence matrix (or unoriented incidence matrix) of G is a p × q matrix
, where p and q are the numbers of vertices
and edges respectively, such that
if the vertex 
and edge 
are incident and 0 otherwise.
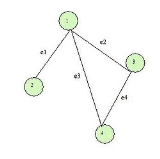
For example the incidence matrix of the undirected graph shown on the right is a matrix consisting of 4 rows (corresponding to the four vertices, 1-4) and 4 columns (corresponding to the four edges, e1-e4):
The incidence matrix of a directed graph
D is a p × q matrix
where p and q are the number of vertices and edges respectively, such that 
if the edge 
leaves vertex 
, 
if it enters vertex 
and 0 otherwise. (Note that many authors use the opposite sign convention.)
An oriented incidence matrix of an undirected graph G is the incidence matrix, in the sense of directed graphs, of any orientation of G. That is, in the column of edge e, there is one +1 in the row corresponding to one vertex of e and one −1 in the row corresponding to the other vertex of e, and all other rows have 0. All oriented incidence matrices of G differ only by negating some set of columns. In many uses, this is an insignificant difference, so one can speak of the oriented incidence matrix, even though that is technically incorrect.
The oriented or unoriented incidence matrix of a graph G is related to the adjacency matrix
of its line graph
L(G) by the following theorem:
where
is the adjacency matrix of the line graph of G, B(G) is the incidence matrix, and 
is the identity matrix
of dimension q.
The Kirchhoff matrix is obtained from the oriented incidence matrix M(G) by the formula
The integral cycle space
of a graph is equal to the null space
of its oriented incidence matrix, viewed as a matrix over the integers or real or complex numbers. The binary cycle space is the null space of its oriented or unoriented incidence matrix, viewed as a matrix over the two-element field
.
that orients the given signed graph. The column of a positive edge has a +1 in the row corresponding to one endpoint and a −1 in the row corresponding to the other endpoint, just like an edge in an ordinary (unsigned) graph. The column of a negative edge has either a +1 or a −1 in both rows. The line graph and Kirchhoff matrix properties generalize to signed graphs.
Multigraph
The definitions of incidence matrix apply to graphs with loops
and multiple edges
. The column of an oriented incidence matrix that corresponds to a loop is all zero, unless the graph is signed and the loop is negative; then the column is all zero except for ±2 in the row of its incident vertex.
can have multiple vertices assigned to one edge; thus, the general case describes a hypergraph.
C is a p × q matrix
, where p and q are the number of points and lines respectively, such that 
if the point 
and line 
are incident and 0 otherwise. In this case the incidence matrix is also a biadjacency matrix of the Levi graph
of the structure. As there is a hypergraph
for every Levi graph, and vice-versa, the incidence matrix of an incidence structure describes a hypergraph.
. For instance, in a finite plane, X is the set of points and Y is the set of lines. In a finite geometry of higher dimension, X could be the set of points and Y could be the set of subspaces of dimension one less than the dimension of Y; or X could be the set of all subspaces of one dimension d and Y the set of all subspaces of another dimension e.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an incidence matrix is a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
that shows the relationship between two classes of objects. If the first class is X and the second is Y, the matrix has one row for each element of X and one column for each element of Y. The entry in row x and column y is 1 if x and y are related (called incident in this context) and 0 if they are not. There are variations; see below.
Undirected and directed graphs
In graph theoryGraph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
an undirected graph G has two kinds of incidence matrices: unoriented and oriented.
The incidence matrix (or unoriented incidence matrix) of G is a p × q matrix
, where p and q are the numbers of verticesVertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
and edges respectively, such that
if the vertex and edge are incident and 0 otherwise.For example the incidence matrix of the undirected graph shown on the right is a matrix consisting of 4 rows (corresponding to the four vertices, 1-4) and 4 columns (corresponding to the four edges, e1-e4):
The incidence matrix of a directed graph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
D is a p × q matrix
where p and q are the number of vertices and edges respectively, such that if the edge leaves vertex , if it enters vertex and 0 otherwise. (Note that many authors use the opposite sign convention.)An oriented incidence matrix of an undirected graph G is the incidence matrix, in the sense of directed graphs, of any orientation of G. That is, in the column of edge e, there is one +1 in the row corresponding to one vertex of e and one −1 in the row corresponding to the other vertex of e, and all other rows have 0. All oriented incidence matrices of G differ only by negating some set of columns. In many uses, this is an insignificant difference, so one can speak of the oriented incidence matrix, even though that is technically incorrect.
The oriented or unoriented incidence matrix of a graph G is related to the adjacency matrix
Adjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
of its line graph
Line graph
In graph theory, the line graph L of undirected graph G is another graph L that represents the adjacencies between edges of G...
L(G) by the following theorem:
where
is the adjacency matrix of the line graph of G, B(G) is the incidence matrix, and is the identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
of dimension q.
The Kirchhoff matrix is obtained from the oriented incidence matrix M(G) by the formula
The integral cycle space
Cycle space
In graph theory, an area of mathematics, a cycle space is a vector space defined from an undirected graph; elements of the cycle space represent formal combinations of cycles in the graph....
of a graph is equal to the null space
Null space
In linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...
of its oriented incidence matrix, viewed as a matrix over the integers or real or complex numbers. The binary cycle space is the null space of its oriented or unoriented incidence matrix, viewed as a matrix over the two-element field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
.
Signed and bidirected graphs
The incidence matrix of a signed graph is a generalization of the oriented incidence matrix. It is the incidence matrix of any bidirected graphBidirected graph
In the mathematical domain of graph theory, a bidirected graph is a graph in which each edge is given an independent orientation at each end...
that orients the given signed graph. The column of a positive edge has a +1 in the row corresponding to one endpoint and a −1 in the row corresponding to the other endpoint, just like an edge in an ordinary (unsigned) graph. The column of a negative edge has either a +1 or a −1 in both rows. The line graph and Kirchhoff matrix properties generalize to signed graphs.
MultigraphMultigraphIn mathematics, a multigraph or pseudograph is a graph which is permitted to have multiple edges, , that is, edges that have the same end nodes. Thus two vertices may be connected by more than one edge....
s
The definitions of incidence matrix apply to graphs with loopsLoop (graph theory)
In graph theory, a loop is an edge that connects a vertex to itself. A simple graph contains no loops....
and multiple edges
Multiple edges
In graph theory, multiple edges , are two or more edges that are incident to the same two vertices...
. The column of an oriented incidence matrix that corresponds to a loop is all zero, unless the graph is signed and the loop is negative; then the column is all zero except for ±2 in the row of its incident vertex.
Hypergraphs
Because the edges of ordinary graphs can only have two vertices (one at each end), the column of an incidence matrix for graphs can only have two non-zero entries. By contrast, a hypergraphHypergraph
In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...
can have multiple vertices assigned to one edge; thus, the general case describes a hypergraph.
Incidence structures
The incidence matrix of an incidence structureIncidence structure
In mathematics, an incidence structure is a tripleC=.\,where P is a set of "points", L is a set of "lines" and I \subseteq P \times L is the incidence relation. The elements of I are called flags. If \in I,...
C is a p × q matrix
, where p and q are the number of points and lines respectively, such that if the point and line are incident and 0 otherwise. In this case the incidence matrix is also a biadjacency matrix of the Levi graphLevi graph
In combinatorial mathematics, a Levi graph or incidence graph is a bipartite graph associated with an incidence structure. From a collection of points and lines in an incidence geometry or a projective configuration, we form a graph with one vertex per point, one vertex per line, and an edge for...
of the structure. As there is a hypergraph
Hypergraph
In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...
for every Levi graph, and vice-versa, the incidence matrix of an incidence structure describes a hypergraph.
Finite geometries
An important example is a finite geometryFinite geometry
A finite geometry is any geometric system that has only a finite number of points.Euclidean geometry, for example, is not finite, because a Euclidean line contains infinitely many points, in fact as many points as there are real numbers...
. For instance, in a finite plane, X is the set of points and Y is the set of lines. In a finite geometry of higher dimension, X could be the set of points and Y could be the set of subspaces of dimension one less than the dimension of Y; or X could be the set of all subspaces of one dimension d and Y the set of all subspaces of another dimension e.