
Hessenberg matrix
Encyclopedia
In linear algebra
, a Hessenberg matrix is a special kind of square matrix, one that is "almost" triangular
. To be exact, an upper Hessenberg matrix has zero entries below the first subdiagonal, and a lower Hessenberg matrix has zero entries above the first superdiagonal. They are named after Karl Hessenberg
.
For example: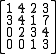
is upper Hessenberg and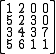
is lower Hessenberg.
s require significantly less computational effort
when applied to triangular matrices
, and this improvement often carries over to Hessenberg matrices as well. If the constraints of a linear algebra problem do not allow a general matrix to be conveniently reduced to a triangular one, reduction to Hessenberg form is often the next best thing. In fact, reduction of any matrix to a Hessenberg form can be achieved in a finite number of steps (for example, through Householder's algorithm
of unitary similarity transforms). Subsequent reduction of Hessenberg matrix to a triangular matrix can be achieved through iterative procedures, such as shifted QR
-factorization. In eigenvalue algorithm
s, the Hessenberg matrix can be further reduced to a triangular matrix through Shifted QR-factorization combined with deflation steps. Reducing a general matrix to a Hessenberg matrix and then reducing further to a triangular matrix, instead of directly reducing a general matrix to a triangular matrix, often economize the arithmetic involved in the QR algorithm
for eigenvalue problems.
A matrix that is both upper Hessenberg and lower Hessenberg is a tridiagonal matrix.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a Hessenberg matrix is a special kind of square matrix, one that is "almost" triangular
Triangular matrix
In the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
. To be exact, an upper Hessenberg matrix has zero entries below the first subdiagonal, and a lower Hessenberg matrix has zero entries above the first superdiagonal. They are named after Karl Hessenberg
Karl Hessenberg
Karl Adolf Hessenberg was a German mathematician and engineer. The Hessenberg matrix form is named after him...
.
For example:
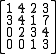
is upper Hessenberg and
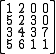
is lower Hessenberg.
Computer programming
Many linear algebra algorithmAlgorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s require significantly less computational effort
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
when applied to triangular matrices
Triangular matrix
In the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
, and this improvement often carries over to Hessenberg matrices as well. If the constraints of a linear algebra problem do not allow a general matrix to be conveniently reduced to a triangular one, reduction to Hessenberg form is often the next best thing. In fact, reduction of any matrix to a Hessenberg form can be achieved in a finite number of steps (for example, through Householder's algorithm
Householder transformation
In linear algebra, a Householder transformation is a linear transformation that describes a reflection about a plane or hyperplane containing the origin. Householder transformations are widely used in numerical linear algebra, to perform QR decompositions and in the first step of the QR algorithm...
of unitary similarity transforms). Subsequent reduction of Hessenberg matrix to a triangular matrix can be achieved through iterative procedures, such as shifted QR
QR decomposition
In linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A=QR of an orthogonal matrix Q and an upper triangular matrix R...
-factorization. In eigenvalue algorithm
Eigenvalue algorithm
In linear algebra, one of the most important problems is designing efficient and stable algorithms for finding the eigenvalues of a matrix. These eigenvalue algorithms may also find eigenvectors.-Characteristic polynomial:...
s, the Hessenberg matrix can be further reduced to a triangular matrix through Shifted QR-factorization combined with deflation steps. Reducing a general matrix to a Hessenberg matrix and then reducing further to a triangular matrix, instead of directly reducing a general matrix to a triangular matrix, often economize the arithmetic involved in the QR algorithm
QR algorithm
In numerical linear algebra, the QR algorithm is an eigenvalue algorithm: that is, a procedure to calculate the eigenvalues and eigenvectors of a matrix. The QR transformation was developed in the late 1950s by John G.F. Francis and by Vera N. Kublanovskaya , working independently...
for eigenvalue problems.
Properties
The product of a Hessenberg matrix with a triangular matrix is again Hessenberg. More precisely, if A is upper Hessenberg and T is upper triangular, then AT and TA are upper Hessenberg.A matrix that is both upper Hessenberg and lower Hessenberg is a tridiagonal matrix.
External links
- Hessenberg matrix at MathWorld.
- Hessenberg matrix at PlanetMath.
- High performance algorithms for reduction to condensed (Hessenberg, tridiagonal, bidiagonal) form

