
Hypercomplex number
Encyclopedia
In mathematics
, a hypercomplex number is a traditional term for an element of an algebra over a field
where the field
is the real number
s or the complex number
s. In the nineteenth century number system
s called quaternion
s, tessarine
s, coquaternion
s, biquaternions, and octonion
s became established concepts in mathematical literature. The concept of a hypercomplex number covered them all, and called for a science to explain and classify them.
The cataloguing project began in 1872 when Benjamin Peirce
first published his Linear Associative Algebra, and was carried forward by his son Charles Sanders Peirce. Most significantly, they identified the nilpotent
and the idempotent as useful hypercomplex numbers for classifications. Hurwitz and Frobenius proved theorems that put limits on hypercomplexity: Hurwitz's theorem (normed division algebras), and Frobenius theorem (real division algebras)
.
It was matrix algebra
that harnessed the hypercomplex systems. First, matrices contributed new hypercomplex numbers like 2 × 2 real matrices. Soon the matrix paradigm began to explain the others as they became represented by matrices and their operations. In 1907 Joseph Wedderburn
showed that associative hypercomplex systems could be represented by matrices, or direct sums of systems of matrices. From that date the preferred term for a hypercomplex system became associative algebra
as seen in the title of Wedderburn’s thesis at University of Edinburgh
. Note however, that non-associative systems like octonions and hyperbolic quaternion
s represent another type of hypercomplex number.
As Hawkins (1972) explains, the hypercomplex numbers are stepping stones to learning about Lie group
s and group representation
theory. For instance, in 1929 Emmy Noether
at Bryn Mawr
wrote on "hypercomplex quantities and representation theory".
Review of the historic particulars gives body to the generalities of modern theory. In 1973 Kantor and Soldovnikov published a textbook on hypercomplex numbers which was translated in 1989; a reviewer says it has a "highly classical flavour". See K.H. Parshall (1985) for a detailed exposition of the heyday of hypercomplex numbers, including the role of such luminaries as Theodor Molien
and Eduard Study
. For the transition to modern algebra, Bartel van der Waerden devotes thirty pages to hypercomplex numbers in his History of Algebra (1985).
 for a basis
for a basis  . It is conventional to normalize the basis so that
. It is conventional to normalize the basis so that  . A technical approach to hypercomplex numbers directs attention first to those of dimension
. A technical approach to hypercomplex numbers directs attention first to those of dimension
two. Higher dimensions are configured as Cliffordian or algebraic sums of other algebras.
Up to isomorphism, there are just three 2-dimensional algebras over the reals: the ordinary complex number
s, the split-complex number
s, and the dual number
s.
with arbitrary real numbers a0 and a1.
Using the common method of completing the square
by
substracting a1u and adding the quadratic complement a1²/4 to both sides yields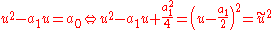 so that
so that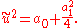
The three cases depend on this real value:
The complex numbers are the only two-dimensional hypercomplex algebra which is a field
.
Algebras such as the split-complex numbers which include non-real roots of 1, also contain idempotents and zero divisor
and zero divisor
s , so such algebras cannot be division algebra
, so such algebras cannot be division algebra
s. However, these properties can turn out to be very meaningful, for instance in describing the Lorentz transformations of special relativity
.
is the unital associative algebra generated over an underlying vector space equipped with a quadratic form
. Over the real numbers this is equivalent to being able to define a symmetric scalar product, u.v = ½(uv + vu) that can be used to orthogonalise the quadratic form, to give a set of bases {e1...ek} such that:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a hypercomplex number is a traditional term for an element of an algebra over a field
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
where the field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
is the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s or the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. In the nineteenth century number system
Number system
In mathematics, a 'number system' is a set of numbers, , together with one or more operations, such as addition or multiplication....
s called quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s, tessarine
Tessarine
In mathematics, a tessarine is a hypercomplex number of the formt = w + x i + y j + z k, \quad w, x, y, z \in Rwhere i j = j i = k, \quad i^2 = -1, \quad j^2 = +1 .The tessarines are best known for their subalgebra of real tessarines t = w + y j \ ,...
s, coquaternion
Coquaternion
In abstract algebra, the split-quaternions or coquaternions are elements of a 4-dimensional associative algebra introduced by James Cockle in 1849 under the latter name. Like the quaternions introduced by Hamilton in 1843, they form a four dimensional real vector space equipped with a...
s, biquaternions, and octonion
Octonion
In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s became established concepts in mathematical literature. The concept of a hypercomplex number covered them all, and called for a science to explain and classify them.
The cataloguing project began in 1872 when Benjamin Peirce
Benjamin Peirce
Benjamin Peirce was an American mathematician who taught at Harvard University for approximately 50 years. He made contributions to celestial mechanics, statistics, number theory, algebra, and the philosophy of mathematics....
first published his Linear Associative Algebra, and was carried forward by his son Charles Sanders Peirce. Most significantly, they identified the nilpotent
Nilpotent
In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
and the idempotent as useful hypercomplex numbers for classifications. Hurwitz and Frobenius proved theorems that put limits on hypercomplexity: Hurwitz's theorem (normed division algebras), and Frobenius theorem (real division algebras)
Frobenius theorem (real division algebras)
In mathematics, more specifically in abstract algebra, the Frobenius theorem, proved by Ferdinand Georg Frobenius in 1877, characterizes the finite-dimensional associative division algebras over the real numbers...
.
It was matrix algebra
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
that harnessed the hypercomplex systems. First, matrices contributed new hypercomplex numbers like 2 × 2 real matrices. Soon the matrix paradigm began to explain the others as they became represented by matrices and their operations. In 1907 Joseph Wedderburn
Joseph Wedderburn
Joseph Henry Maclagan Wedderburn was a Scottish mathematician, who taught at Princeton University for most of his career. A significant algebraist, he proved that a finite division algebra is a field, and part of the Artin–Wedderburn theorem on simple algebras...
showed that associative hypercomplex systems could be represented by matrices, or direct sums of systems of matrices. From that date the preferred term for a hypercomplex system became associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
as seen in the title of Wedderburn’s thesis at University of Edinburgh
University of Edinburgh
The University of Edinburgh, founded in 1583, is a public research university located in Edinburgh, the capital of Scotland, and a UNESCO World Heritage Site. The university is deeply embedded in the fabric of the city, with many of the buildings in the historic Old Town belonging to the university...
. Note however, that non-associative systems like octonions and hyperbolic quaternion
Hyperbolic quaternion
In the abstract algebra of algebras over a field, the hyperbolic quaternionq = a + bi + cj + dk, \quad a,b,c,d \in R \!is a mutated quaternion wherei^2 = j^2 = k^2 = +1 \! instead of the usual −1....
s represent another type of hypercomplex number.
As Hawkins (1972) explains, the hypercomplex numbers are stepping stones to learning about Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s and group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
theory. For instance, in 1929 Emmy Noether
Emmy Noether
Amalie Emmy Noether was an influential German mathematician known for her groundbreaking contributions to abstract algebra and theoretical physics. Described by David Hilbert, Albert Einstein and others as the most important woman in the history of mathematics, she revolutionized the theories of...
at Bryn Mawr
Bryn Mawr College
Bryn Mawr College is a women's liberal arts college located in Bryn Mawr, a community in Lower Merion Township, Pennsylvania, ten miles west of Philadelphia. The name "Bryn Mawr" means "big hill" in Welsh....
wrote on "hypercomplex quantities and representation theory".
Review of the historic particulars gives body to the generalities of modern theory. In 1973 Kantor and Soldovnikov published a textbook on hypercomplex numbers which was translated in 1989; a reviewer says it has a "highly classical flavour". See K.H. Parshall (1985) for a detailed exposition of the heyday of hypercomplex numbers, including the role of such luminaries as Theodor Molien
Theodor Molien
Theodor Molien or Fedor Eduardovich Molin was a Baltic-German mathematician. He was born in Riga, Latvia, which at that time was a part of Russian Empire. Molien studied associative algebras and polynomial invariants of finite groups.-Youth in Riga:Theodor Molien's father Eduard Molien was a...
and Eduard Study
Eduard Study
Eduard Study was a German mathematician known for work on invariant theory of ternary forms and for the study of spherical trigonometry. He is also known for contributions to space geometry, hypercomplex numbers, and criticism of early physical chemistry.Study was born in Coburg in the Duchy of...
. For the transition to modern algebra, Bartel van der Waerden devotes thirty pages to hypercomplex numbers in his History of Algebra (1985).
Catalogue
A definition of hypercomplex number is given by as finite dimensional algebras over the reals that are unital and distributive (but not necessarily associative). Elements are generated with real number coefficients for a basis
for a basis  . It is conventional to normalize the basis so that
. It is conventional to normalize the basis so that  . A technical approach to hypercomplex numbers directs attention first to those of dimension
. A technical approach to hypercomplex numbers directs attention first to those of dimensionDimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
two. Higher dimensions are configured as Cliffordian or algebraic sums of other algebras.
Two-dimensional real algebras
Theorem:Up to isomorphism, there are just three 2-dimensional algebras over the reals: the ordinary complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, the split-complex number
Split-complex number
In abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...
s, and the dual number
Dual number
In linear algebra, the dual numbers extend the real numbers by adjoining one new element ε with the property ε2 = 0 . The collection of dual numbers forms a particular two-dimensional commutative unital associative algebra over the real numbers. Every dual number has the form z = a + bε with a and...
s.
- proof: Since the algebra is closedClosure (mathematics)In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
under squaring, and it has but two dimensions, the non-real basis element u squares to an arbitrary linear combination of 1 and u: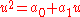
with arbitrary real numbers a0 and a1.
Using the common method of completing the square
Completing the square
In elementary algebra, completing the square is a technique for converting a quadratic polynomial of the formax^2 + bx + c\,\!to the formIn this context, "constant" means not depending on x. The expression inside the parenthesis is of the form ...
by
substracting a1u and adding the quadratic complement a1²/4 to both sides yields
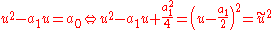 so that
so that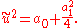
The three cases depend on this real value:
- If 4a0 = −, the above formula yields ũ2 = 0. Hence, ũ can directly be identified with the nilpotentNilpotentIn mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
element of the Dual numbers' basis
of the Dual numbers' basis 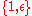 .
. - If 4a0 > −, the above formula yields ũ2 > 0. This leads to the split-complex numbers which have normalized basis
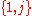 with
with 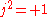 . To obtain j from ũ, the latter must be divided by the positive real number
. To obtain j from ũ, the latter must be divided by the positive real number  which has the same square as ũ.
which has the same square as ũ. - If 4a0 < −, the above formula yields ũ2 < 0. This leads to the complex numbers which have normalized basis
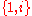 with
with  . To yield i from ũ, the latter has to be divided by a positive real number
. To yield i from ũ, the latter has to be divided by a positive real number 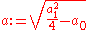 which squares to the negative of ũ2.
which squares to the negative of ũ2.
The complex numbers are the only two-dimensional hypercomplex algebra which is a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
.
Algebras such as the split-complex numbers which include non-real roots of 1, also contain idempotents
 and zero divisor
and zero divisorZero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s
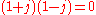 , so such algebras cannot be division algebra
, so such algebras cannot be division algebraDivision algebra
In the field of mathematics called abstract algebra, a division algebra is, roughly speaking, an algebra over a field, in which division is possible.- Definitions :...
s. However, these properties can turn out to be very meaningful, for instance in describing the Lorentz transformations of special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
.
Clifford algebras
Clifford algebraClifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
is the unital associative algebra generated over an underlying vector space equipped with a quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
. Over the real numbers this is equivalent to being able to define a symmetric scalar product, u.v = ½(uv + vu) that can be used to orthogonalise the quadratic form, to give a set of bases {e1...ek} such that:
-

Imposing closure under multiplication now generates a multivector space spanned by 2k bases, {1, e1, e2, e3, ... , e1e2, ... , e1e2e3, ...}. These can be interpreted as the bases of a hypercomplex number system. Unlike the bases {e1...ek}, the remaining bases may or may not anti-commute, depending on how many simple exchanges must be carried out to swap the two factors. So e1e2 = - e2e1; but e1(e2e3) = + (e2e3)e1.
Putting aside the bases for which ei2 = 0 (ie directions in the original space over which the quadratic form was degenerateDegenerate formIn mathematics, specifically linear algebra, a degenerate bilinear form ƒ on a vector space V is one such that the map from V to V^* given by v \mapsto is not an isomorphism...
), the remaining Clifford algebras can be identified by the label Cℓp,q(R) indicating that the algebra is constructed from p simple bases with ei2 = +1, q with ei2 = -1, and where R indicates that this is to be a Clifford algebra over the reals—i.e. coefficients of elements of the algebra are to be real numbers.
These algebras, called geometric algebraGeometric algebraGeometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
s, form a systematic set which turn out to be very useful in physics problems which involve rotationRotationA rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
s, phasePhase (waves)Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
s, or spinSpin (physics)In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
s, notably in classicalClassical mechanicsIn physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
and quantum mechanicsQuantum mechanicsQuantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, electromagnetic theory and relativityTheory of relativityThe theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
.
Examples include: the complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s Cℓ0,1(R); split-complex numberSplit-complex numberIn abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...
s Cℓ1,0(R); quaternionQuaternionIn mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s Cℓ0,2(R); split-biquaternions Cℓ0,3(R); coquaternionCoquaternionIn abstract algebra, the split-quaternions or coquaternions are elements of a 4-dimensional associative algebra introduced by James Cockle in 1849 under the latter name. Like the quaternions introduced by Hamilton in 1843, they form a four dimensional real vector space equipped with a...
s Cℓ1,1(R) ≈ Cℓ2,0(R) (the natural algebra of 2d space); Cℓ3,0(R) (the natural algebra of 3d space, and the algebra of the Pauli matricesPauli matricesThe Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
); and Cℓ1,3(R) the space-time algebra.
The elements of the algebra Cℓp,q(R) form an even subalgebra Cℓ0q+1,p(R) of the algebra Cℓq+1,p(R), which can be used to parametrise rotations in the larger algebra. There is thus a close connection between complex numbers and rotations in 2D space; between quaternions and rotations in 3D space; between split-complex numbers and (hyperbolic) rotations (Lorentz transformations) in 1+1 D space, and so on.
Whereas Cayley–Dickson and split-complex constructs with eight or more dimensions are not associative anymore with respect to multiplication, Clifford algebras retain associativity at any dimensionality.
In 1995 Ian R. PorteousIan R. PorteousIan Robertson Porteous was a Scottish mathematician at the University of Liverpool and an educator on Merseyside. He is best known for three books on geometry and modern algebra...
wrote on "The recognition of subalgebras" in his book on Clifford algebras. His Proposition 11.4 summarizes the hypercomplex cases:
- Let A be a real associative algebra with unit element 1. Then
- 1 generates R (algebra of real numbersReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
),
- any two-dimensional subalgebra generated by an element e0 of A such that e02 = −1 is isomorphic to C (algebra of complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s),
- any two-dimensional subalgebra generated by an element e0 of A such that e02 = 1 is isomorphic to 2R (algebra of split-complex numbersSplit-complex numberIn abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...
),
- any four-dimensional subalgebra generated by a set {e0, e1} of mutually anti-commuting elements of A such that
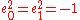 is isomorphic to H (algebra of quaternionsQuaternionIn mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
is isomorphic to H (algebra of quaternionsQuaternionIn mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
),
- any four-dimensional subalgebra generated by a set {e0, e1} of mutually anti-commuting elements of A such that
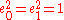 is isomorphic to R(2) (2 × 2 real matrices, coquaternionCoquaternionIn abstract algebra, the split-quaternions or coquaternions are elements of a 4-dimensional associative algebra introduced by James Cockle in 1849 under the latter name. Like the quaternions introduced by Hamilton in 1843, they form a four dimensional real vector space equipped with a...
is isomorphic to R(2) (2 × 2 real matrices, coquaternionCoquaternionIn abstract algebra, the split-quaternions or coquaternions are elements of a 4-dimensional associative algebra introduced by James Cockle in 1849 under the latter name. Like the quaternions introduced by Hamilton in 1843, they form a four dimensional real vector space equipped with a...
s),
- any eight-dimensional subalgebra generated by a set {e0, e1,e2} of mutually anti-commuting elements of A such that
 is isomorphic to 2H (split-biquaternions),
is isomorphic to 2H (split-biquaternions),
- any eight-dimensional subalgebra generated by a set {e0, e1,e2} of mutually anti-commuting elements of A such that
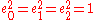 is isomorphic to C(2) (biquaternions, Pauli algebra, 2 × 2 complex matrices).
is isomorphic to C(2) (biquaternions, Pauli algebra, 2 × 2 complex matrices).
For extension beyond the classical algebras, see Classification of Clifford algebrasClassification of Clifford algebrasIn abstract algebra, in particular in the theory of nondegenerate quadratic forms on vector spaces, the structures of finite-dimensional real and complex Clifford algebras have been completely classified...
.
Cayley–Dickson construction
All of the Clifford algebras Cℓp,q(R) apart from the complex numbers and the quaternions contain non-real elements j that square to 1; and so cannot be division algebras. A different approach to extending the complex numbers is taken by the Cayley–Dickson construction. This generates number systems of dimension 2n, n in {2, 3, 4, ...}, with bases , where all the non-real bases anti-commute and satisfy
, where all the non-real bases anti-commute and satisfy  . These are non-associative in dimension at least 8.
. These are non-associative in dimension at least 8.
The first algebras in this sequence are the four-dimensional quaternionQuaternionIn mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s, eight-dimensional octonionOctonionIn mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s, and 16-dimensional sedenionSedenionIn abstract algebra, sedenions form a 16-dimensional non-associative algebra over the reals obtained by applying the Cayley–Dickson construction to the octonions...
s. However, satisfying these requirements comes at a price: Each increase in dimensionality introduces new algebraic complications. Quaternion multiplication is not commutative anymore, octonion multiplication is non-associative, and the normedNorm (mathematics)In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
of sedenionSedenionIn abstract algebra, sedenions form a 16-dimensional non-associative algebra over the reals obtained by applying the Cayley–Dickson construction to the octonions...
s is not multiplicative.
The Cayley–Dickson construction can be modified by inserting an extra sign at some stages. This leads to coquaternionCoquaternionIn abstract algebra, the split-quaternions or coquaternions are elements of a 4-dimensional associative algebra introduced by James Cockle in 1849 under the latter name. Like the quaternions introduced by Hamilton in 1843, they form a four dimensional real vector space equipped with a...
s (split-quaternions; e.g. to bases with
with  ) and split-octonionSplit-octonionIn mathematics, the split-octonions are a nonassociative extension of the quaternions . They differ from the octonions in the signature of quadratic form: the split-octonions have a split-signature whereas the octonions have a positive-definite signature .The split-octonions form the unique split...
) and split-octonionSplit-octonionIn mathematics, the split-octonions are a nonassociative extension of the quaternions . They differ from the octonions in the signature of quadratic form: the split-octonions have a split-signature whereas the octonions have a positive-definite signature .The split-octonions form the unique split...
s (e.g. to bases with
with 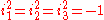 ,
, 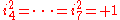 ). The coquaternions contain nilpotentNilpotentIn mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
). The coquaternions contain nilpotentNilpotentIn mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
s, have a non-commutative multiplication, and are isomorphic to the 2 × 2 real matrices. Split-octonions are non-associative.
Tensor products
The tensor product of any two algebras is another algebra, which can be used to produce many more examples of hypercomplex number systems.
In particular taking tensor products with the complex numbers leads to four-dimensional tessarineTessarineIn mathematics, a tessarine is a hypercomplex number of the formt = w + x i + y j + z k, \quad w, x, y, z \in Rwhere i j = j i = k, \quad i^2 = -1, \quad j^2 = +1 .The tessarines are best known for their subalgebra of real tessarines t = w + y j \ ,...
s , eight-dimensional biquaternions
, eight-dimensional biquaternions  , and 16-dimensional complex octonionOctonionIn mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
, and 16-dimensional complex octonionOctonionIn mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s .
.
Tessarines offer a commutative and associative multiplication, biquaternions are associative but not commutative, and conic sedenions are not associative and not commutative. They all contain idempotents and zero-divisors, but offer a multiplicative modulusAbsolute valueIn mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
. Biquaternions contain nilpotents, conic sedenions are also not power associativePower associativityIn abstract algebra, power associativity is a property of a binary operation which is a weak form of associativity.An algebra is said to be power-associative if the subalgebra generated by any element is associative....
.
Further examples
- bicomplex numbers - a 4d vector space over the reals, or 2d over the complex numbers
- multicomplex numbers - 2(n-1)-dimensional vector spaces over the complex numbers
- Tricomplex numberTricomplex numberIn mathematics, the tricomplex numbers are a three-dimensional hypercomplex number system developed by Silviu Olariu in his book Complex Numbers in n Dimensions .-Definition:...
s - a 3d vector space over the reals, one of a family of systems of commutative hypercomplex numbers in n-dimensions over the reals.
External links

