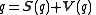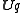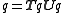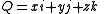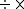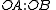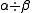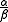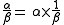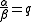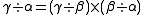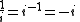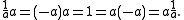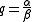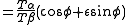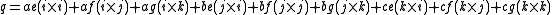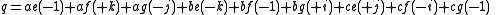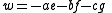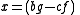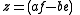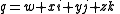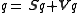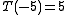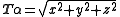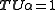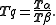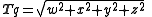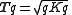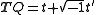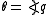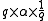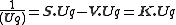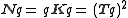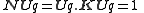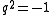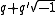Classical Hamiltonian quaternions
Encyclopedia
William Rowan Hamilton
invented quaternions, a mathematical entity in 1843. This article describes Hamilton's original treatment of quaternions, using his notation and terms. Hamilton's treatment is more geometric
than the modern approach, which emphasizes quaternions' algebra
ic properties. Mathematically, quaternions discussed here are those used in almost all modern applications.
A quaternion can be represented as the sum of a scalar
and a vector. It can also be represented as the product of its tensor
and its versor.
Hamilton's conceived a vector as the "difference of its two extreme points. For Hamilton, a vector was always a three-dimensional entity, having three co-ordinates relative to any given co-ordinate system, including but not limited to both polar
and rectangular systems. He therefore referred to vectors as "triplets".
Hamilton defined addition of vectors in geometric terms, by placing the origin
of the second vector at the end of the first. He went on to define vector subtraction.
By adding a vector to itself multiple times, he defined multiplication of a vector by an integer
, then extended this to division by an integer, and multiplication (and division) of a vector by a rational number. Finally, by taking limits, he defined the result of multiplying a vector α by any scalar x as a vector β with the same direction as α if x is positive; the opposite direction to α if x is negative; and a length that is |x| times the length of α.
The quotient
of two parallel
or anti-parallel vectors is therefore a scalar with absolute value equal to the ratio of the lengths of the two vectors; the scalar is positive if the vectors are parallel and negative if they are anti-parallel.
Hamilton introduced the term tensor in his first book, Lectures on Quaternions, based on lectures he gave given shortly after his invention of the quaternions:
Each quaternion has a tensor, which is a measure of its magnitude (in the same way as the length of a vector is a measure of a vectors' magnitude). When a quaternion is defined as the quotient of two vectors, its tensor is the ratio of the lengths of these vectors.
In general a Versor can be associated with a plane, an axis and an angle.
When a versor and a vector which lies in the plane of the versor are multiplied, the result is a new vector of the same length but turned by the angle of the versor.
, and since a versor can be thought of as the quotient of two vectors, a versor has a representative great circle
arc, called a vector arc, connecting these two points, drawn from the divisor or lower part of quotient, to the dividend or upper part of the quotient.
, then it is called a right versor, a right radial or quadrantal versor.
Unlike other versors, these two cannot be represented by a unique arc. The arc of one is a single point, and minus one can be represented by an infinite number of arcs, because there are an infinite number of shortest lines between antipodal points of a sphere.
These two operations S and V are called "take the Scalar of" and "take the vector of" a quaternion. The vector part of a quaternion is also called the right part.
Every quaternion is equal to a versor multiplied by the tensor of the quaternion. Denoting the versor of a quaternion by
we have
The angle of a right quaternion is 90 degrees. A right quaternion can also be thought of as a vector plus a zero scalar. Right quaternions may be put in what was called the standard trinomial form. For example, if Q is a right quaternion, it may be written as:
In particular it is important to understand that there is a single operation of multiplication, a single operation of division, and a single operations of addition and subtraction. This single multiplication operator can operate on any of the types of mathematical entities. Likewise every kind of entity can be divided, added or subtracted from any other type of entity. Understanding the meaning of the subtraction symbol is critical in quaternion theory, because it leads to an understanding of the concept of a vector.
These marks are:
"...characteristics of synthesis and analysis of a state of progression, according as this state is considered as being derived from, or compared with, some other state of that progression."
called ordinal analysis
The first example of subtraction is to take the point A to represent the earth, and the point B to represent the sun, then an arrow drawn from A to B represents the act of moving or vection from A to B.
this represents the first example in Hamilton's lectures of a vector. In this case the act of traveling from the earth to the moon.
Vectors and scalars can be added. When a vector is added to a scalar, a completely different entity, a quaternion is created.
A vector plus a scalar is always a quaternion even if the scalar is zero. If the scalar added to the vector is zero then the new quaternion produced is called a right quaternion. It has an angle characteristic of 90 degrees.
It is not required to learn the following more advanced terms in order to use division and multiplication.
Division is a kind of analysis
called cardinal analysis. Multiplication is a kind of synthesis
called cardinal synthesis
If OA and OB represent two vectors drawn from the origin O to two other points A and B, then the geometric fraction was written as
Alternately if the two vectors are represented by α and β the quotient was written as
or
Hamilton asserts: "The quotient of two vectors is generally a quaternion". Lectures on Quaternions also first introduces the concept of a quaternion as the quotient of two vectors:
Logically and by definition,
if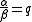
then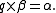
.
In Hamilton's calculus the product is not commutative, i.e., the order of the variables is of great importance. If the order of q and β were to be reversed the result would not in general be α. The quaternion q can be thought of as an operator that changes β into α, by first rotating it, formerly an act of version and then changing the length of it, formerly call an act of tension.
Also by definition the quotient of two vectors is equal to the numerator times the reciprocal
of the denominator. Since multiplication of vectors is not commutative, the order cannot be changed in the following expression.
Again the order of the two quantities on the right hand side is significant.
Hardy presents the definition of division in terms of pneumonic cancellation rules. "Canceling being performed by an upward right hand stroke".
If alpha and beta are vectors and q is a quaternion such that
then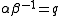
and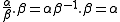
and
An important way to think of q is as an operator that changes β into α, by first rotating it (version) and then changing its length (tension).
William Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
invented quaternions, a mathematical entity in 1843. This article describes Hamilton's original treatment of quaternions, using his notation and terms. Hamilton's treatment is more geometric
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
than the modern approach, which emphasizes quaternions' algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
ic properties. Mathematically, quaternions discussed here are those used in almost all modern applications.
Classical elements of a quaternion
Hamilton defined a quaternion as the quotient of two directed lines in tridimensional space; or, more generally, as the quotient of two vectors.A quaternion can be represented as the sum of a scalar
Scalar
Scalar may refer to:*Scalar , a quantity used to multiply vectors in the context of vector spaces*Scalar , a quantity which is independent of specific classes of coordinate systems...
and a vector. It can also be represented as the product of its tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
and its versor.
Scalar
Hamilton invented the term scalars for the real numbers, because they span the "scale of progression from positive to negative infinity" or because they represent the "comparison of positions upon one common scale". Hamilton regarded ordinary scalar algebra as the science of pure time.Vector
Hamilton defined a vector as "a right line ... having not only length but also direction". Hamilton derived the word vector from the Latin vehere, to carry.Hamilton's conceived a vector as the "difference of its two extreme points. For Hamilton, a vector was always a three-dimensional entity, having three co-ordinates relative to any given co-ordinate system, including but not limited to both polar
Polar coordinate system
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a fixed point and an angle from a fixed direction....
and rectangular systems. He therefore referred to vectors as "triplets".
Hamilton defined addition of vectors in geometric terms, by placing the origin
Origin
Origin, origins, or original may refer to:- Beginning of the universe and life :* Abiogenesis, the study of how life on Earth arose from inanimate matter* Cosmogony, any theory concerning the origin of the universe...
of the second vector at the end of the first. He went on to define vector subtraction.
By adding a vector to itself multiple times, he defined multiplication of a vector by an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
, then extended this to division by an integer, and multiplication (and division) of a vector by a rational number. Finally, by taking limits, he defined the result of multiplying a vector α by any scalar x as a vector β with the same direction as α if x is positive; the opposite direction to α if x is negative; and a length that is |x| times the length of α.
The quotient
Quotient
In mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
of two parallel
Parallel (geometry)
Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
or anti-parallel vectors is therefore a scalar with absolute value equal to the ratio of the lengths of the two vectors; the scalar is positive if the vectors are parallel and negative if they are anti-parallel.
Unit vector
A unit vector is a vector of length one. Examples of unit vectors include i,j and k.Tensor
Hamilton defines tensor as a positive numerical quantity, or more properly signless, number. A tensor can be thought of as a positive scalar. The "tensor" can be thought of as representing a "stretching factor."Hamilton introduced the term tensor in his first book, Lectures on Quaternions, based on lectures he gave given shortly after his invention of the quaternions:
- it seems convenient to enlarge by definition the signification of the new word tensor, so as to render it capable of including also those other cases in which we operate on a line by diminishing instead of increasing its length ; and generally by altering that length in any definite ratio. We shall thus (as was hinted at the end of the article in question) have fractional and even incommensurableCommensurability (mathematics)In mathematics, two non-zero real numbers a and b are said to be commensurable if a/b is a rational number.-History of the concept:...
tensors, which will simply be numerical multipliers, and will all be positive or (to speak more properly) SignLess Numbers, that is, unclothed with the algebraic signs of positive and negative ; because, in the operation here considered, we abstract from the directions (as well as from the situations) of the lines which are compared or operated on.
Each quaternion has a tensor, which is a measure of its magnitude (in the same way as the length of a vector is a measure of a vectors' magnitude). When a quaternion is defined as the quotient of two vectors, its tensor is the ratio of the lengths of these vectors.
Versor
A versor is a quaternion with a tensor of 1. Alternatively, a versor can be defined as the quotient of two equal-length vectors.In general a Versor can be associated with a plane, an axis and an angle.
When a versor and a vector which lies in the plane of the versor are multiplied, the result is a new vector of the same length but turned by the angle of the versor.
Vector arc
Since every unit vector can be thought of as a point on a unit sphereUnit sphere
In mathematics, a unit sphere is the set of points of distance 1 from a fixed central point, where a generalized concept of distance may be used; a closed unit ball is the set of points of distance less than or equal to 1 from a fixed central point...
, and since a versor can be thought of as the quotient of two vectors, a versor has a representative great circle
Great circle
A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
arc, called a vector arc, connecting these two points, drawn from the divisor or lower part of quotient, to the dividend or upper part of the quotient.
Right versor
When the arc of a versor has the magnitude of a right angleRight angle
In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...
, then it is called a right versor, a right radial or quadrantal versor.
Degenerate forms
Two special degenerate versor cases, called the unit-scalars These two scalars, negative and positive unity can be thought of as scalar quaternions. These two scalars are special limiting cases, corresponding to versors with angles of either zero or π.Unlike other versors, these two cannot be represented by a unique arc. The arc of one is a single point, and minus one can be represented by an infinite number of arcs, because there are an infinite number of shortest lines between antipodal points of a sphere.
Quaternion
Every quaternion can be decomposed into a scalar and a vector.
These two operations S and V are called "take the Scalar of" and "take the vector of" a quaternion. The vector part of a quaternion is also called the right part.
Every quaternion is equal to a versor multiplied by the tensor of the quaternion. Denoting the versor of a quaternion by
we have
Right quaternion
A right quaternion is a quaternion whose scalar component is zero,
The angle of a right quaternion is 90 degrees. A right quaternion can also be thought of as a vector plus a zero scalar. Right quaternions may be put in what was called the standard trinomial form. For example, if Q is a right quaternion, it may be written as:
Four operations
Four operations are of fundamental importance in quaternion notation.
In particular it is important to understand that there is a single operation of multiplication, a single operation of division, and a single operations of addition and subtraction. This single multiplication operator can operate on any of the types of mathematical entities. Likewise every kind of entity can be divided, added or subtracted from any other type of entity. Understanding the meaning of the subtraction symbol is critical in quaternion theory, because it leads to an understanding of the concept of a vector.
Ordinal operators
The two ordinal operations in classical quaternion notation were addition and subtraction or + and -.These marks are:
"...characteristics of synthesis and analysis of a state of progression, according as this state is considered as being derived from, or compared with, some other state of that progression."
Subtraction
Subtraction is a type of analysisAnalysis
Analysis is the process of breaking a complex topic or substance into smaller parts to gain a better understanding of it. The technique has been applied in the study of mathematics and logic since before Aristotle , though analysis as a formal concept is a relatively recent development.The word is...
called ordinal analysis
Ordinal analysis
In proof theory, ordinal analysis assigns ordinals to mathematical theories as a measure of their strength. The field was formed when Gerhard Gentzen in 1934 used cut elimination to prove, in modern terms, that the proof theoretic ordinal of Peano arithmetic is ε0.-Definition:Ordinal...
...let space be now regarded as the field of progression which is to be studied, and POINTS as states of that progression. ...I am led to regard the word "Minus," or the mark -, in geometry, as the sign or characteristic of analysis of one geometric position (in space), as compared with another (such) position. The comparison of one mathematical point with another with a view to the determination of what may be called their ordinal relation, or their relative position in space...
The first example of subtraction is to take the point A to represent the earth, and the point B to represent the sun, then an arrow drawn from A to B represents the act of moving or vection from A to B.
-
- B - A
this represents the first example in Hamilton's lectures of a vector. In this case the act of traveling from the earth to the moon.
Addition of vectors and scalars
Vectors and scalars can be added. When a vector is added to a scalar, a completely different entity, a quaternion is created.
A vector plus a scalar is always a quaternion even if the scalar is zero. If the scalar added to the vector is zero then the new quaternion produced is called a right quaternion. It has an angle characteristic of 90 degrees.
Cardinal operations
The two Cardinal operations in quaternion notation are geometric multiplication and geometric division and can be written:
It is not required to learn the following more advanced terms in order to use division and multiplication.
Division is a kind of analysis
Analysis
Analysis is the process of breaking a complex topic or substance into smaller parts to gain a better understanding of it. The technique has been applied in the study of mathematics and logic since before Aristotle , though analysis as a formal concept is a relatively recent development.The word is...
called cardinal analysis. Multiplication is a kind of synthesis
Synthesis
In general, the noun synthesis refers to a combination of two or more entities that together form something new; alternately, it refers to the creating of something by artificial means...
called cardinal synthesis
Division
Classically, the quaternion was viewed as the ratio of two vectors, sometimes called a geometric fraction.If OA and OB represent two vectors drawn from the origin O to two other points A and B, then the geometric fraction was written as
Alternately if the two vectors are represented by α and β the quotient was written as
or
Hamilton asserts: "The quotient of two vectors is generally a quaternion". Lectures on Quaternions also first introduces the concept of a quaternion as the quotient of two vectors:
Logically and by definition,
if
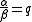
then
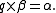.In Hamilton's calculus the product is not commutative, i.e., the order of the variables is of great importance. If the order of q and β were to be reversed the result would not in general be α. The quaternion q can be thought of as an operator that changes β into α, by first rotating it, formerly an act of version and then changing the length of it, formerly call an act of tension.
Also by definition the quotient of two vectors is equal to the numerator times the reciprocal
Reciprocal
-In mathematics:*Multiplicative inverse, in mathematics, the number 1/x, which multiplied by x gives the product 1, also known as a reciprocal*Reciprocal rule, a technique in calculus for calculating derivatives of reciprocal functions...
of the denominator. Since multiplication of vectors is not commutative, the order cannot be changed in the following expression.
Again the order of the two quantities on the right hand side is significant.
Hardy presents the definition of division in terms of pneumonic cancellation rules. "Canceling being performed by an upward right hand stroke".
If alpha and beta are vectors and q is a quaternion such that
then
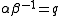
and
-
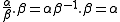
and 
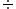are inverse operations, such that:
-
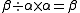and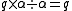 
and
An important way to think of q is as an operator that changes β into α, by first rotating it (version) and then changing its length (tension).
Division of the unit vectors i, j, k
The results of the using the division operator on i,j and k was as follows.
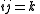
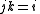
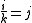
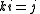
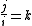
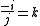
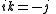
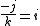
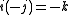
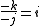
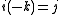
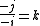
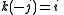
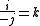
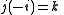
The reciprocal of a unit vector is the vector reversed.
Because a unit vector and its reciprocal are parallel to each other but point in opposite directions, the product of a unit vector and its reciprocal have a special case commutative property, for example if a is any unit vector then:
However in the more general case involving more than one vector (whether or not it is a unit vector) the commutative property does not hold. For example:
-
≠ 
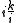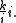
This is because k/i is carefully defined as:
-
.
So that:
-
,
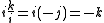however
Division of two parallel vectors
While in general the quotient of two vectors is a quaternion, If α and β are two parallel vectors then the quotient of these two vectors is a scalar. For example if
,
and
then
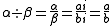
Where a/b is a scalar.
Division of two non-parallel vectors
The quotient of two vectors is in general the quaternion:
Where α and β are two non-parallel vectors, φ is that angle between them, and e is a unit vector perpendicular to the plane of the vectors α and β, with its direction given by the standard right hand rule.
Multiplication
Classical quaternion notation had only one concept of multiplication. Multiplication of two real numbers, two imaginary numbers or a real number by an imaginary number in the classical notation system was the same operation.
Multiplication of a scalar and a vector was accomplished with the same single multiplication operator; multiplication of two vectors of quaternions used this same operation as did multiplication of a quaternion and a vector or of two quaternions.
Factor, Faciend and Factum
-
- Factor x Faciend = Factum
When two quantities are multiplied the first quantity is called the factor, the second quantity is called the faciend and the result is called the factum.
Distributive
In classical notation, multiplication was distributive. Understanding this makes it simple to see why the product of two vectors in classical notation produced a quaternion.
Using the quaternion multiplication table we have:
Then collecting terms:
The first three terms are a scalar.
Letting
So that the product of two vectors is a quaternion, and can be written in the form:
Product of two right quaternion
The product of two Right Quaternions is generally a quaternion.
Let α and β be the right quaternions that result from taking the vectors of two quaternions:
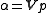
Their product in general is a new quaternion represented here by r. This product is not ambiguous because classical notation has only one product.
Like all quaternions r may now be decomposed into its vector and scalar parts.
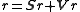
The terms on the right are called scalar of the product, and the vector of the product of two right quaternions.
Scalar and vector
Two important operations in two the classical quaternion notation system were S(q) and V(q) which meant take the scalar part of, and take the imaginary part, what Hamilton called the vector part of the quaternion. Here S and V are operators acting on q. Parenthesis can be omitted in these kinds of expressions without ambiguity. Classical notation:
Here, q is a quaternion. Sq is the scalar of the quaternion while Vq is the vector of the quaternion.
Conjugate
K is the conjugate operator. The conjugate of a quaternion is a quaternion obtained by multiplying the vector part of the first quaternion by minus one.
If
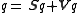
then
.
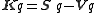The expression
,
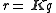means, assign the quaternion r the value of the conjugate of the quaternion q.
Tensor
T is the tensor operator. It returns a kind of number called a tensor.
The tensor of a positive scalar is that scalar. The tensor of a negative scalar is the absolute valueAbsolute valueIn mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of the scalar (i.e., without the negative sign). For example:
The tensor of a vector is by definition the length of the vector. For example if:
Then
The tensor of a unit vector is one. Since the versor of a vector is a unit vector, the tensor of the versor of any vector is always equal to unity. Symbolically:
A quaternion is by definition the quotient of two vectors and the tensor of a quaternion is by definition the quotient of the tensors of these two vectors. In symbols:
From this definition it can be shown that a useful formula for the tensor of a quaternion is:
It can also be proven from this definition that another formula to obtain the tensor of a quaternion is from the common norm, defined as the product of a quaternion and its conjugate. The square root of the common norm of a quaternion is equal to its tensor.
A useful identity is that the square of the tensor of a quaternion is equal to the tensor of the square of a quaternion, so that parenthesis may be omitted.
Also, the tensors of conjugate quaternions are equal.
If Q is a biquaternion then its tensor is a bitensor.
Here t and t' are real numbers.
Axis and angle
Taking the angle of a non-scalar quaternion, resulted in a value greater than zero and less than π.
When a non-scalar quaternion is viewed as the quotient of two vectors, then the axis of the quaternion is a unit vector perpendicular to the plane of the two vectors in this original quotient, in a direction specified by the right hand rule.
The angle is the angle between the two vectors.
In symbols,
Reciprocal
If
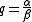
then its reciprocalReciprocal-In mathematics:*Multiplicative inverse, in mathematics, the number 1/x, which multiplied by x gives the product 1, also known as a reciprocal*Reciprocal rule, a technique in calculus for calculating derivatives of reciprocal functions...
is defined as
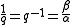
The expression:
Reciprocals have many important applications, for example rotationsQuaternions and spatial rotationUnit quaternions provide a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. Compared to Euler angles they are simpler to compose and avoid the problem of gimbal lock. Compared to rotation matrices they are more numerically stable and may...
, particularly when q is a versor. A versor has an easy formula for its reciprocal.
In words the reciprocal of a versor is equal to its conjugate. The dots between operators show the order to of the operations, and also help to indicate that S and U for example, are two different operations rather than a single operation named SU.
Common norm
The product of a quaternion with its conjugate is its common norm.
The operation of taking the common norm of a quaternion is represented with the letter N. By definition the common norm is the product of a quaternion with its conjugate. It can be proven that common norm is equal to the square of the tensor of a quaternion. However this proof does not constitute a definition. Hamilton gives exact, independent definitions of both the common norm and the tensor. This norm was adopted as suggested from the theory of numbers, however to quote Hamilton "they will not often be wanted". The tensor is generally of greater utility. The word norm does not appear in Lectures on Quaternions, and only twice in the table of contents of Elements of Quaternions.
In symbols:
The common norm of a versor is always equal to positive unity.
Geometrically real and geometrically imaginary numbers
In classical quaternion literature the equation
was thought to have infinitely many solutions that were called geometrically real.
These solutions are the unit vectors that form the surface of a unit sphere.
A geometrically real quaternion is one that can be written as a linear combination of i, j and k, such that the squares of the coefficientCoefficientIn mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s add up to one. Hamilton demonstrated that there had to be additional roots of this equation in addition to the geometrically real roots. Given the existence of the imaginary scalar, a number of expressions can be written and given proper names. All of these were part of Hamilton's original quaternion calculus. In symbols:
where q and q' are real quaternions, and the square root of minus one is the imaginary of ordinary algebra, and are called an imaginary or symbolical roots and not a geometrically real vector quantity.
Imaginary scalar
Geometrically Imaginary quantities are additional roots of the above equation of a purely symbolic nature. In article 214 of Elements Hamilton proves that if there is an i j and k there also has to be another quantity h which is an imaginary scalar, which he observes should have already occurred to anyone who had read the preceding articles with attention. Article 149 of Elements is about Geometrically Imaginary numbers and includes a footnote introducing the term biquaternion. The terms imaginary of ordinary algebra and scalar imaginary are sometimes used for these geometrically imaginary quantities.
Geometrically Imaginary roots to an equation were interpreted in classical thinking as geometrically impossible situations. Article 214 of elements of quaternions explores the example of the equation of a line and a circle that do not intersect, as being indicated by the equation having only a geometrically imaginary root.
In Hamilton's later writings he proposed using the letter h to denote the imaginary scalar
Bi-vector
Article 214 also defines a bivector as the product of a vector and the imaginary of ordinary algebra.
Biquaternion
A Biquaternion is by definition the quotient of a bivector and a vector. It can also be written in this same form.
Other double quaternions
Hamilton invented the term associative to distinguish between the imaginary scalar, which is both commutative and associative, and four other possible roots of negative unity which he designated L M N and O, mentioning them briefly in appendix B of Lectures on Quaternions and in private letters. However, non-associative roots of minus one do not appear in Elements of Quaternions. Hamilton died before he worked on these strange entities. His son claimed it to be a "bow for another Ulysses".
See also
- Cayley–Dickson construction
- OctonionOctonionIn mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s - Frobenius theoremFrobenius theorem (real division algebras)In mathematics, more specifically in abstract algebra, the Frobenius theorem, proved by Ferdinand Georg Frobenius in 1877, characterizes the finite-dimensional associative division algebras over the real numbers...
-
