.gif)
Lattice (group)
Encyclopedia
In mathematics
, especially in geometry
and group theory
, a lattice in Rn is a discrete subgroup of Rn which spans
the real
vector space
Rn. Every lattice in Rn can be generated from a basis
for the vector space by forming all linear combination
s with integer
coefficients. A lattice may be viewed as a regular tiling of a space by a primitive cell
.
Lattices have many significant applications in pure mathematics, particularly in connection to Lie algebra
s, number theory
and group theory. They also arise in applied mathematics in connection with coding theory
, in cryptography
because of conjectured computational hardness of several lattice problems
, and are used in various ways in the physical sciences. For instance, in materials science
and solid-state physics
, a lattice is a synonym for the "frame work" of a crystalline structure, a 3-dimensional array of regularly spaced points coinciding with the atom
or molecule
positions in a crystal
. More generally, lattice models
are studied in physics
, often by the techniques of computational physics
.
of discrete translational symmetry
in n directions. A pattern with this lattice of translational symmetry cannot have more, but may have less symmetry than the lattice itself.
A lattice in the sense of a 3-dimension
al array of regularly spaced points coinciding with e.g. the atom
or molecule
positions in a crystal
, or more generally, the orbit of a group action
under translational symmetry, is a translate of the translation lattice: a coset
, which need not contain the origin, and therefore need not be a lattice in the previous sense.
A simple example of a lattice in Rn is the subgroup Zn. A more complicated example is the Leech lattice
, which is a lattice in R24. The period lattice in R2 is central to the study of elliptic functions, developed in nineteenth century mathematics; it generalises to higher dimensions in the theory of abelian functions.

where {v1, ..., vn} is a basis for Rn. Different bases can generate the same lattice, but the absolute value
of the determinant
of the vectors vi is uniquely determined by Λ, and is denoted by d(Λ).
If one thinks of a lattice as dividing the whole of Rn into equal polyhedra
(copies of an n-dimensional parallelepiped
, known as the fundamental region of the lattice), then d(Λ) is equal to the n-dimensional volume
of this polyhedron. This is why d(Λ) is sometimes called the covolume of the lattice.
relates the number d(Λ) and the volume of a symmetric convex set
S to the number of lattice points contained in S. The number of lattice points contained in a polytope
all of whose vertices are elements of the lattice is described by the polytope's Ehrhart polynomial
. Formulas for some of the coefficients of this polynomial involve d(Λ) as well.
Theorem: let P be the polytope: fundamental region of a basis which is a weighted square self-blocking clutter S.
then covolume(P) = k and P contains k - 1 integer interior points, where k is the wheight of the edges of S.
.
. Below, the wallpaper group
of the lattice is given in parentheses; note that a pattern with this lattice of translational symmetry cannot have more, but may have less symmetry than the lattice itself. If the symmetry group of a pattern contains an n-fold rotation then the lattice has n-fold symmetry for even n and 2n-fold for odd n.
For the classification of a given lattice, start with one point and take a nearest second point. For the third point, not on the same line, consider its distances to both points. Among the points for which the smaller of these two distances is least, choose a point for which the larger of the two is least. (Not logically equivalent
but in the case of lattices giving the same result is just "Choose a point for which the larger of the two is least".)
The five cases correspond to the triangle
being equilateral, right isosceles, right, isosceles, and scalene. In a rhombic lattice, the shortest distance may either be a diagonal or a side of the rhombus, i.e., the line segment connecting the first two points may or may not be one of the equal sides of the isosceles triangle. This depends on the smaller angle of the rhombus being less than 60° or between 60° and 90°.
The general case is known as a period lattice. If the vectors p and q generate the lattice, instead of p and q we can also take p and p-q, etc. In general in 2D, we can take a p + b q and c p + d q for integers a,b, c and d such that ad-bc is 1 or -1. This ensures that p and q themselves are integer linear combinations of the other two vectors. Each pair p, q defines a parallelogram, all with the same area, the magnitude of the cross product
. One parallelogram fully defines the whole object. Without further symmetry, this parallelogram is a fundamental parallelogram.
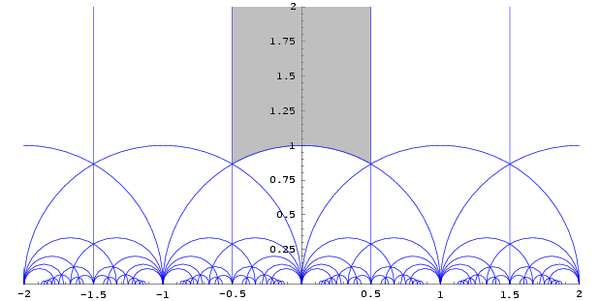 The vectors p and q can be represented by complex numbers. Up to size and orientation, a pair can be represented by their quotient. Expressed geometrically: if two lattice points are 0 and 1, we consider the position of a third lattice point. Equivalence in the sense of generating the same lattice is represented by the modular group
The vectors p and q can be represented by complex numbers. Up to size and orientation, a pair can be represented by their quotient. Expressed geometrically: if two lattice points are 0 and 1, we consider the position of a third lattice point. Equivalence in the sense of generating the same lattice is represented by the modular group
: represents choosing a different third point in the same grid,
represents choosing a different third point in the same grid,  represents choosing a different side of the triangle as reference side 0-1, which in general implies changing the scaling of the lattice, and rotating it. Each "curved triangle" in the image contains for each 2D lattice shape one complex number, the grey area is a canonical representation, corresponding to the classification above, with 0 and 1 two lattice points that are closest to each other; duplication is avoided by including only half of the boundary. The rhombic lattices are represented by the points on its boundary, with the hexagonal lattice as vertex, and i for the square lattice. The rectangular lattices are at the imaginary axis, and the remaining area represents the parallelogrammetic lattices, with the mirror image of a parallelogram represented by the mirror image in the imaginary axis.
represents choosing a different side of the triangle as reference side 0-1, which in general implies changing the scaling of the lattice, and rotating it. Each "curved triangle" in the image contains for each 2D lattice shape one complex number, the grey area is a canonical representation, corresponding to the classification above, with 0 and 1 two lattice points that are closest to each other; duplication is avoided by including only half of the boundary. The rhombic lattices are represented by the points on its boundary, with the hexagonal lattice as vertex, and i for the square lattice. The rectangular lattices are at the imaginary axis, and the remaining area represents the parallelogrammetic lattices, with the mirror image of a parallelogram represented by the mirror image in the imaginary axis.
. 3D patterns with translational symmetry of a particular type cannot have more, but may have less symmetry than the lattice itself.
For example, the Gaussian integer
s form a lattice in C.
Every lattice in Rn is a free abelian group
of rank
n; every lattice in Cn is a free abelian group of rank 2n.
G is a discrete subgroup, such that the quotient
G/Γ is of finite measure, for the measure on it inherited from Haar measure
on G (left-invariant, or right-invariant—the definition is independent of that choice). That will certainly be the case when G/Γ is compact
, but that sufficient condition is not necessary, as is shown by the case of the modular group
in SL2(R), which is a lattice but where the quotient isn't compact (it has cusps). There are general results stating the existence of lattices in Lie groups.
A lattice is said to be uniform or cocompact if G/Γ is compact; otherwise the lattice is called non-uniform.
 lattices in
lattices in  this concept can be generalised to any finite dimensional vector space
this concept can be generalised to any finite dimensional vector space
over any field
. This can be done as follows:
Let be a field
be a field
, let be an
be an  -dimensional
-dimensional  -vector space
-vector space
, let be a
be a  -basis
-basis
for and let
and let  be a ring
be a ring
contained within . Then the
. Then the  lattice
lattice  in
in  generated by
generated by  is given by:
is given by:

Different bases will in general generate different lattices. However, if the transition matrix
will in general generate different lattices. However, if the transition matrix  between the bases is in
between the bases is in  - the general linear group
- the general linear group
of R (in simple terms this means that all the entries of are in
are in  and all the entries of
and all the entries of  are in
are in  - which is equivalent to saying that the determinant
- which is equivalent to saying that the determinant
of is in
is in  - the unit group of elements in
- the unit group of elements in  with multiplicative inverses) then the lattices generated by these bases will be isomorphic since
with multiplicative inverses) then the lattices generated by these bases will be isomorphic since  induces an isomorphism
induces an isomorphism
between the two lattices.
Important cases of such lattices occur in number theory with K a p-adic field and R the p-adic integers.
For a vector space which is also an inner product space
, the dual lattice can be concretely described by the set:
or equivalently as,

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
and group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, a lattice in Rn is a discrete subgroup of Rn which spans
Linear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
the real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
Rn. Every lattice in Rn can be generated from a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
for the vector space by forming all linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
s with integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
coefficients. A lattice may be viewed as a regular tiling of a space by a primitive cell
Primitive cell
Used predominantly in geometry, solid state physics, and mineralogy, particularly in describing crystal structure, a primitive cell is a minimum cell corresponding to a single lattice point of a structure with translational symmetry in 2 dimensions, 3 dimensions, or other dimensions...
.
Lattices have many significant applications in pure mathematics, particularly in connection to Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s, number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
and group theory. They also arise in applied mathematics in connection with coding theory
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
, in cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
because of conjectured computational hardness of several lattice problems
Lattice problems
In computer science, lattice problems are a class of optimization problems on lattices. The conjectured intractability of such problems is central to construction of secure lattice-based cryptosystems...
, and are used in various ways in the physical sciences. For instance, in materials science
Materials science
Materials science is an interdisciplinary field applying the properties of matter to various areas of science and engineering. This scientific field investigates the relationship between the structure of materials at atomic or molecular scales and their macroscopic properties. It incorporates...
and solid-state physics
Solid-state physics
Solid-state physics is the study of rigid matter, or solids, through methods such as quantum mechanics, crystallography, electromagnetism, and metallurgy. It is the largest branch of condensed matter physics. Solid-state physics studies how the large-scale properties of solid materials result from...
, a lattice is a synonym for the "frame work" of a crystalline structure, a 3-dimensional array of regularly spaced points coinciding with the atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
or molecule
Molecule
A molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
positions in a crystal
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
. More generally, lattice models
Lattice model (physics)
In physics, a lattice model is a physical model that is defined on a lattice, as opposed to the continuum of space or spacetime. Lattice models originally occurred in the context of condensed matter physics, where the atoms of a crystal automatically form a lattice. Currently, lattice models are...
are studied in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, often by the techniques of computational physics
Computational physics
Computational physics is the study and implementation of numerical algorithms to solve problems in physics for which a quantitative theory already exists...
.
Symmetry considerations and examples
A lattice is the symmetry groupSymmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of discrete translational symmetry
Translational symmetry
In geometry, a translation "slides" an object by a a: Ta = p + a.In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation...
in n directions. A pattern with this lattice of translational symmetry cannot have more, but may have less symmetry than the lattice itself.
A lattice in the sense of a 3-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al array of regularly spaced points coinciding with e.g. the atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
or molecule
Molecule
A molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
positions in a crystal
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
, or more generally, the orbit of a group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
under translational symmetry, is a translate of the translation lattice: a coset
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
, which need not contain the origin, and therefore need not be a lattice in the previous sense.
A simple example of a lattice in Rn is the subgroup Zn. A more complicated example is the Leech lattice
Leech lattice
In mathematics, the Leech lattice is an even unimodular lattice Λ24 in 24-dimensional Euclidean space E24 found by .-History:Many of the cross-sections of the Leech lattice, including the Coxeter–Todd lattice and Barnes–Wall lattice, in 12 and 16 dimensions, were found much earlier than...
, which is a lattice in R24. The period lattice in R2 is central to the study of elliptic functions, developed in nineteenth century mathematics; it generalises to higher dimensions in the theory of abelian functions.
Dividing space according to a lattice
A typical lattice Λ in Rn thus has the form
where {v1, ..., vn} is a basis for Rn. Different bases can generate the same lattice, but the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the vectors vi is uniquely determined by Λ, and is denoted by d(Λ).
If one thinks of a lattice as dividing the whole of Rn into equal polyhedra
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
(copies of an n-dimensional parallelepiped
Parallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...
, known as the fundamental region of the lattice), then d(Λ) is equal to the n-dimensional volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
of this polyhedron. This is why d(Λ) is sometimes called the covolume of the lattice.
Lattice points in convex sets
Minkowski's theoremMinkowski's theorem
In mathematics, Minkowski's theorem is the statement that any convex set in Rn which is symmetric with respect to the origin and with volume greater than 2n d contains a non-zero lattice point...
relates the number d(Λ) and the volume of a symmetric convex set
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
S to the number of lattice points contained in S. The number of lattice points contained in a polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
all of whose vertices are elements of the lattice is described by the polytope's Ehrhart polynomial
Ehrhart polynomial
In mathematics, an integral polytope has an associated Ehrhart polynomial which encodes the relationship between the volume of a polytope and the number of integer points the polytope contains...
. Formulas for some of the coefficients of this polynomial involve d(Λ) as well.
Theorem: let P be the polytope: fundamental region of a basis which is a weighted square self-blocking clutter S.
then covolume(P) = k and P contains k - 1 integer interior points, where k is the wheight of the edges of S.
- See also: Integer points in polyhedra
Computing with lattices
Lattice basis reduction is the problem of finding a short and nearly orthogonal lattice basis. The Lenstra-Lenstra-Lovász lattice basis reduction algorithm (LLL) approximates such a lattice basis in polynomial time; it has found numerous applications, particularly in public-key cryptographyPublic-key cryptography
Public-key cryptography refers to a cryptographic system requiring two separate keys, one to lock or encrypt the plaintext, and one to unlock or decrypt the cyphertext. Neither key will do both functions. One of these keys is published or public and the other is kept private...
.
Lattices in two dimensions: detailed discussion
There are five 2D lattice types as given by the crystallographic restriction theoremCrystallographic restriction theorem
The crystallographic restriction theorem in its basic form was based on the observation that the rotational symmetries of a crystal are usually limited to 2-fold, 3-fold, 4-fold, and 6-fold...
. Below, the wallpaper group
Wallpaper group
A wallpaper group is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...
of the lattice is given in parentheses; note that a pattern with this lattice of translational symmetry cannot have more, but may have less symmetry than the lattice itself. If the symmetry group of a pattern contains an n-fold rotation then the lattice has n-fold symmetry for even n and 2n-fold for odd n.
- a rhombicRhombusIn Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...
lattice, also called centered rectangular lattice or isosceles triangularTriangleA triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
lattice (cmm), with evenly spaced rows of evenly spaced points, with the rows alternatingly shifted one half spacing (symmetrically staggered rows):
-
-
- a hexagonal latticeHexagonal latticeThe hexagonal lattice or equilateral triangular lattice is one of the five 2D lattice types.Three nearby points form an equilateral triangle. In images four orientations of such a triangle are by far the most common...
or equilateral triangular lattice (p6m)
- a hexagonal lattice
-
- a square latticeSquare latticeIn mathematics, the square lattice is a type of lattice in a two-dimensional Euclidean space. It is the two-dimensional version of the integer lattice. It is one of the five types of two-dimensional lattices as classified by their symmetry groups; its symmetry group is known symbolically as p4m.Two...
(p4m):
- a square lattice
-
- a rectangularRectangleIn Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
lattice, also called primitive rectangular lattice (pmm):
- a rectangular
-
- more generally, a parallelogramParallelogramIn Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...
mic lattice, also called oblique lattice (p2)(with asymmetrically staggered rows):
- more generally, a parallelogram
-
For the classification of a given lattice, start with one point and take a nearest second point. For the third point, not on the same line, consider its distances to both points. Among the points for which the smaller of these two distances is least, choose a point for which the larger of the two is least. (Not logically equivalent
Logical equivalence
In logic, statements p and q are logically equivalent if they have the same logical content.Syntactically, p and q are equivalent if each can be proved from the other...
but in the case of lattices giving the same result is just "Choose a point for which the larger of the two is least".)
The five cases correspond to the triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
being equilateral, right isosceles, right, isosceles, and scalene. In a rhombic lattice, the shortest distance may either be a diagonal or a side of the rhombus, i.e., the line segment connecting the first two points may or may not be one of the equal sides of the isosceles triangle. This depends on the smaller angle of the rhombus being less than 60° or between 60° and 90°.
The general case is known as a period lattice. If the vectors p and q generate the lattice, instead of p and q we can also take p and p-q, etc. In general in 2D, we can take a p + b q and c p + d q for integers a,b, c and d such that ad-bc is 1 or -1. This ensures that p and q themselves are integer linear combinations of the other two vectors. Each pair p, q defines a parallelogram, all with the same area, the magnitude of the cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
. One parallelogram fully defines the whole object. Without further symmetry, this parallelogram is a fundamental parallelogram.

Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
:
 represents choosing a different third point in the same grid,
represents choosing a different third point in the same grid,  represents choosing a different side of the triangle as reference side 0-1, which in general implies changing the scaling of the lattice, and rotating it. Each "curved triangle" in the image contains for each 2D lattice shape one complex number, the grey area is a canonical representation, corresponding to the classification above, with 0 and 1 two lattice points that are closest to each other; duplication is avoided by including only half of the boundary. The rhombic lattices are represented by the points on its boundary, with the hexagonal lattice as vertex, and i for the square lattice. The rectangular lattices are at the imaginary axis, and the remaining area represents the parallelogrammetic lattices, with the mirror image of a parallelogram represented by the mirror image in the imaginary axis.
represents choosing a different side of the triangle as reference side 0-1, which in general implies changing the scaling of the lattice, and rotating it. Each "curved triangle" in the image contains for each 2D lattice shape one complex number, the grey area is a canonical representation, corresponding to the classification above, with 0 and 1 two lattice points that are closest to each other; duplication is avoided by including only half of the boundary. The rhombic lattices are represented by the points on its boundary, with the hexagonal lattice as vertex, and i for the square lattice. The rectangular lattices are at the imaginary axis, and the remaining area represents the parallelogrammetic lattices, with the mirror image of a parallelogram represented by the mirror image in the imaginary axis.Lattices in three dimensions
The 14 lattice types in 3D are called Bravais lattices. They are characterized by their space groupSpace group
In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...
. 3D patterns with translational symmetry of a particular type cannot have more, but may have less symmetry than the lattice itself.
Lattices in complex space
A lattice in Cn is a discrete subgroup of Cn which spans the 2n-dimensional real vector space Cn.For example, the Gaussian integer
Gaussian integer
In number theory, a Gaussian integer is a complex number whose real and imaginary part are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as Z[i]. The Gaussian integers are a special case of the quadratic...
s form a lattice in C.
Every lattice in Rn is a free abelian group
Free abelian group
In abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
of rank
Rank of an abelian group
In mathematics, the rank, Prüfer rank, or torsion-free rank of an abelian group A is the cardinality of a maximal linearly independent subset. The rank of A determines the size of the largest free abelian group contained in A. If A is torsion-free then it embeds into a vector space over the...
n; every lattice in Cn is a free abelian group of rank 2n.
In Lie groups
More generally, a lattice Γ in a Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
G is a discrete subgroup, such that the quotient
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
G/Γ is of finite measure, for the measure on it inherited from Haar measure
Haar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
on G (left-invariant, or right-invariant—the definition is independent of that choice). That will certainly be the case when G/Γ is compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, but that sufficient condition is not necessary, as is shown by the case of the modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
in SL2(R), which is a lattice but where the quotient isn't compact (it has cusps). There are general results stating the existence of lattices in Lie groups.
A lattice is said to be uniform or cocompact if G/Γ is compact; otherwise the lattice is called non-uniform.
Lattices over general vector-spaces
Whilst we normally consider lattices in
lattices in  this concept can be generalised to any finite dimensional vector space
this concept can be generalised to any finite dimensional vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over any field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
. This can be done as follows:
Let
 be a field
be a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, let
 be an
be an  -dimensional
-dimensional  -vector space
-vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, let
 be a
be a  -basis
-basisBasis
Basis may refer to* Cost basis, in income tax law, the original cost of property adjusted for factors such as depreciation.* Basis of futures, the value differential between a future and the spot price...
for
 and let
and let  be a ring
be a ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
contained within
 . Then the
. Then the  lattice
lattice  in
in  generated by
generated by  is given by:
is given by:
Different bases
 will in general generate different lattices. However, if the transition matrix
will in general generate different lattices. However, if the transition matrix  between the bases is in
between the bases is in  - the general linear group
- the general linear groupGeneral linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
of R (in simple terms this means that all the entries of
 are in
are in  and all the entries of
and all the entries of  are in
are in  - which is equivalent to saying that the determinant
- which is equivalent to saying that the determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of
 is in
is in  - the unit group of elements in
- the unit group of elements in  with multiplicative inverses) then the lattices generated by these bases will be isomorphic since
with multiplicative inverses) then the lattices generated by these bases will be isomorphic since  induces an isomorphism
induces an isomorphismIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
between the two lattices.
Important cases of such lattices occur in number theory with K a p-adic field and R the p-adic integers.
For a vector space which is also an inner product space
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
, the dual lattice can be concretely described by the set:

or equivalently as,

See also
- Lattice (order)Lattice (order)In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
- Reciprocal latticeReciprocal latticeIn physics, the reciprocal lattice of a lattice is the lattice in which the Fourier transform of the spatial function of the original lattice is represented. This space is also known as momentum space or less commonly k-space, due to the relationship between the Pontryagin duals momentum and...
- Unimodular latticeUnimodular latticeIn mathematics, a unimodular lattice is a lattice of determinant 1 or −1.The E8 lattice and the Leech lattice are two famous examples.- Definitions :...
- Crystal systemCrystal systemIn crystallography, the terms crystal system, crystal family, and lattice system each refer to one of several classes of space groups, lattices, point groups, or crystals...
- Mahler's compactness theoremMahler's compactness theoremIn mathematics, Mahler's compactness theorem, proved by , is a foundational result on lattices in Euclidean space, characterising sets of lattices that are 'bounded' in a certain definite sense. Looked at another way, it explains the ways in which a lattice could degenerate in a sequence of...
- Lattice graphLattice graphThe terms lattice graph, mesh graph, or grid graph refer to a number of categories of graphs whose drawing corresponds to some grid/mesh/lattice, i.e., its vertices correspond to the nodes of the mesh and its edges correspond to the ties between the nodes.-Square grid graph:A common type of a...
- Lattice-based cryptography

