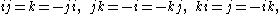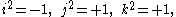Coquaternion - AbsoluteAstronomy.com

Coquaternion multiplication
×	1	i	j	k
1	1	i	j	k
i	i	−1	k	−j
j	j	−k	+1	−i
k	k	j	i	+1

In abstract algebra

Abstract algebra

Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...

, the split-quaternions or coquaternions are elements of a 4-dimensional associative algebra

Associative algebra

In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...

introduced by James Cockle in 1849 under the latter name. Like the quaternion

Quaternion

In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...

s introduced by Hamilton

William Rowan Hamilton

Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...

in 1843, they form a four dimension

Dimension

In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...

al real vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

equipped with a multiplicative operation. Unlike the quaternion algebra, the split-quaternions contain zero divisor

Zero divisor

In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...

s, nilpotent

Nilpotent

In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....

elements, and nontrivial idempotents. As a mathematical structure

Mathematical structure

In mathematics, a structure on a set, or more generally a type, consists of additional mathematical objects that in some manner attach to the set, making it easier to visualize or work with, or endowing the collection with meaning or significance....

, they form an algebra over the real numbers

Algebra over a field

In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...

, which is isomorphic to the algebra of 2 × 2 real matrices. The coquaternions came to be called split-quaternions due to the division into positive and negative terms in the modulus function. For other names for split-quaternions see the Synonyms section below.

The set

forms a basis

Basis (linear algebra)

In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...

. The products of these elements are

and hence ijk = 1. It follows from the defining relations that the set

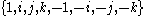is a group under coquaternion multiplication; it is isomorphic to the dihedral group

Dihedral group

In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...

of a square.

A coquaternion

has a conjugate

and multiplicative modulus
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...

.

This quadratic form

Quadratic form

In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....

is split into positive and negative parts, in contrast to the positive definite form on the algebra of quaternions.

When the modulus is non-zero, then q has a multiplicative inverse

Multiplicative inverse

In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...

, namely q*/qq*.

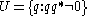
is the set of units

Unit (ring theory)

In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...

. The set P of all coquaternions forms a ring

Ring theory

In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...

(P, +, •) with group

Group (mathematics)

In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...

of units (U, •). The coquaternions with modulus qq* = 1 form a non-compact

Compact space

In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...

topological group

Topological group

In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...

SU(1,1), shown below to be isomorphic to SL(2,R).

The split-quaternion basis can be identified as the basis elements of either the Clifford algebra

Clifford algebra

In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...

Cℓ_1,1(R), with {1, e₁=i, e₂=j, e₁e₂=k}; or the algebra Cℓ_2,0(R), with {1, e₁=j, e₂=k, e₁e₂=i}.

Historically coquaternions preceded Cayley's

Arthur Cayley

Arthur Cayley F.R.S. was a British mathematician. He helped found the modern British school of pure mathematics....

matrix algebra; coquaternions (along with quaternions and tessarine

Tessarine

In mathematics, a tessarine is a hypercomplex number of the formt = w + x i + y j + z k, \quad w, x, y, z \in Rwhere i j = j i = k, \quad i^2 = -1, \quad j^2 = +1 .The tessarines are best known for their subalgebra of real tessarines t = w + y j \ ,...

s) evoked the broader linear algebra

Linear algebra

Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...

Matrix representations

Let

where u and v are ordinary complex number

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

s. Then the complex matrix

,

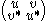with

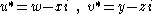
(complex conjugate

Complex conjugate

In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...

s of u and v),
represents q in the ring of matrices in the sense that multiplication of split-quaternions behaves the same way as the matrix multiplication

Matrix multiplication

In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...

.
For example, the determinant

Determinant

In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...

of this matrix is

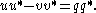
The appearance of the minus sign, where there is a plus in H, distinguishes coquaternions from quaternions. The use of the split-quaternions of modulus one (q q* = 1)
for hyperbolic motions of the Poincaré disk model

Poincaré disk model

In geometry, the Poincaré disk model, also called the conformal disk model, is a model of n-dimensional hyperbolic geometry in which the points of the geometry are in an n-dimensional disk, or unit ball, and the straight lines of the hyperbolic geometry are segments of circles contained in the disk...

of hyperbolic geometry

Hyperbolic geometry

In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...

is one of the great utilities of the algebra.

Besides the complex matrix representation, another linear representation associates coquaternions with 2 × 2 real matrices. This isomorphism can be made explicit as follows: Note first the product

and that the square of each factor on the left is the identity matrix, while the square of the right hand side is the negative of the identity matrix. Furthermore, note that these three matrices, together with the identity matrix, form a basis for M(2,R). One can make the matrix product above correspond to j k = −i in the coquaternion ring. Then for an arbitrary matrix there is the bijection

Bijection

A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...

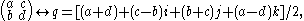
which is in fact a ring isomorphism.
Furthermore, computing squares of components and gathering terms shows that

, which is the determinant of the matrix. Consequently there is a group isomorphism between the unit quasi-sphere of coquaternions and SL2(R) = {g ∈ M(2,R) : det g = 1 }, and hence also with SU(1,1): the latter can be seen in the complex representation above.

For instance, see Karzel and Kist (1985) for the hyperbolic motion group representation with 2 × 2 real matrices.

Profile

The coquaternions may be given polar decomposition by delineation of subalgebras:
Let

r(θ) = j cos θ + k sin θ (here θ is as fundamental as azimuth)

p(a, r) = i sinh a + r cosh a

v(a, r) = i cosh a + r sinh a

These are the equilateral-hyperboloidal coordinates described by Alexander Macfarlane

Alexander Macfarlane

Alexander Macfarlane was a Nova Scotia lawyer and political figure. He was a member of the Canadian Senate from 1870 to 1898. His surname also appears as McFarlane in some sources....

.

Next, form three foundational sets in the vector-subspace of the ring:

E = { r ∈ P: r = r(θ), 0 ≤ θ < 2 π}

J = {p(a, r) ∈ P: a ∈ R, r ∈ E} catenoid

Catenoid

A catenoid is a three-dimensional surface made by rotating a catenary curve about its directrix. Not counting the plane, it is the first minimal surface to be discovered. It was found and proved to be minimal by Leonhard Euler in 1744. Early work on the subject was published also by Jean Baptiste...

I = {v(a, r) ∈ P: a ∈ R, r ∈ E} hyperboloid of two sheets.

Now it is easy to verify that

{q ∈ P: q² = + 1} = J ∪ {1, -1}

and that

{q ∈ P: q² = −1} = I.

These set equalities mean that when p ∈ J then the plane

{x + yp: x, y ∈ R} = D_p

is a subring

Subring

In mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...

of P that is isomorphic to the plane of split-complex number

Split-complex number

In abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...

s just as when v is in I then

{x + yv: x, y ∈ R} = C_v

is a planar subring of P that is isomorphic to the ordinary complex plane

Complex plane

In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...

C.

Note that for every r ∈ E, (r + i)² = 0 = (r − i)² so that r + i and r − i are nilpotents. The plane N = {x + y(r + i): x, y ∈ R} is a subring of P that is isomorphic to the dual numbers. Since every coquaternion must lie in a D_p, a C_v, or an N plane, these planes profile P. For example, the unit quasi-sphere

SU(1, 1) = {q ∈ P: qq* = 1}

consists of the "unit circles" in the constituent planes of P: In D_p it is a unit hyperbola

Unit hyperbola

In geometry, the unit hyperbola is the set of points in the Cartesian plane that satisfies x^2 - y^2 = 1 . In the study of indefinite orthogonal groups, the unit hyperbola forms the basis for an alternative radial lengthWhereas the unit circle surrounds its center, the unit hyperbola requires the...

, in N the "unit circle" is a pair of parallel lines, while in C_v it is indeed a circle (though it appears elliptical due to v-stretching).These ellipse/circles found in each C_v are like the illusion of the Rubin vase

Rubin vase

Rubin's vase is a famous set of ambiguous or bi-stable two-dimensional forms developed around 1915 by the Danish psychologist Edgar Rubin...

which "presents the viewer with a mental choice of two interpretations, each of which is valid".

Pan-orthogonality

When coquaternion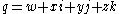

, then the scalar part
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....

of q is w.

Definition: For non-zero coquaternions q and t we write q ⊥ t when the scalar part of the product

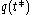is zero.

For every v ∈ I, if q, t ∈ C_v, then q ⊥ t means the rays from 0 to q and t are perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...

.
For every p ∈ J, if q, t ∈ D_p, then q ⊥ t means these two points are hyperbolic-orthogonal
Hyperbolic-orthogonal
In plane geometry, two lines are hyperbolic orthogonal when they are reflections of each other over the asymptote of a given hyperbola.Two particular hyperbolas are frequently used in the plane: x y = 1 with y = 0 as asymptote.Two particular hyperbolas are frequently used in the plane: x y = 1 ...

.
For every r ∈ E and every a ∈ R, p = p(a, r) and v = v(a, r) satisfy p ⊥ v.
If u is a unit in the coquaternion ring, then q ⊥ t implies qu ⊥ tu.

Proof:

follows from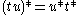

, which can be established using the anticommutativity

Anticommutativity

In mathematics, anticommutativity is the property of an operation that swapping the position of any two arguments negates the result. Anticommutative operations are widely used in algebra, geometry, mathematical analysis and, as a consequence, in physics: they are often called antisymmetric...

property of vector cross product

Cross product

In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...

Counter-sphere geometry

Tak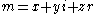e

where

. Fix theta (θ) and suppose

.

Since points on the counter-sphere must line on a counter-circle in some plane
D_p ⊂ P, m can be written, for some p ∈ J

.

Let φ be the angle between the hyperbolas from r to p and m. This angle can be
viewed, in the plane tangent

Tangent

In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...

to the counter-sphere at r, by projection:

.

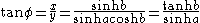As b gets large, tanh b nears one. Then tan φ = 1/sinh a . This appearance of the
angle of parallelism

Angle of parallelism

In hyperbolic geometry, the angle of parallelism φ, also known as Π, is the angle at one vertex of a right hyperbolic triangle that has two asymptotic parallel sides. The angle depends on the segment length a between the right angle and the vertex of the angle of parallelism φ...

in a meridian θ inclines one to expect to see the counter-
sphere unfold as the manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

S¹ × H² where H² is the
hyperbolic plane

Hyperbolic manifold

In mathematics, a hyperbolic n-manifold is a complete Riemannian n-manifold of constant sectional curvature -1.Every complete, connected, simply-connected manifold of constant negative curvature −1 is isometric to the real hyperbolic space Hn. As a result, the universal cover of any closed manifold...

Application to kinematics

By using the foundations given above, one can show that the mapping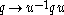

is an ordinary or hyperbolic rotation according as

.

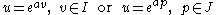These mappings are projectivities in the inversive ring geometry

Inversive ring geometry

In mathematics, inversive ring geometry is the extension of the concepts of projective line, homogeneous coordinates, projective transformations, and cross-ratio to the context of associative rings, concepts usually built upon rings that happen to be fields....

of coquaternions. The
collection of these mappings bears some relation to the Lorentz group

Lorentz group

In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...

since it is also
composed of ordinary and hyperbolic rotations. Among the peculiarities of this approach
to relativistic kinematic is the anisotropic profile, say as compared to
hyperbolic quaternion

Hyperbolic quaternion

In the abstract algebra of algebras over a field, the hyperbolic quaternionq = a + bi + cj + dk, \quad a,b,c,d \in R \!is a mutated quaternion wherei^2 = j^2 = k^2 = +1 \! instead of the usual −1....

s.

Reluctance to use coquaternions for kinematic models may stem from the (2, 2) signature when spacetime

Spacetime

In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...

is presumed to have signature (1, 3) or
(3, 1). Nevertheless, a transparently relativistic kinematics

Kinematics

Kinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....

appears when a point of the
counter-sphere is used to represent an inertial frame of reference

Inertial frame of reference

In physics, an inertial frame of reference is a frame of reference that describes time homogeneously and space homogeneously, isotropically, and in a time-independent manner.All inertial frames are in a state of constant, rectilinear motion with respect to one another; they are not...

. Indeed, if

,
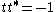then there is a p = i sinh(a) + r cosh(a) ∈ J such that t ∈ D_p, and an b ∈
R such that t = p exp(bp). Then if u = exp(bp), v = i cosh(a) + r sinh(a), and s = ir, the set {t, u, v, s} is a
pan-orthogonal basis stemming from t, and the orthogonalities persist through applications of the ordinary or hyperbolic rotations.

Historical notes

The coquaternions were initially introduced (under that name) in 1849 by James Cockle in the London–Edinburgh–Dublin Philosophical Magazine

Philosophical Magazine

The Philosophical Magazine is one of the oldest scientific journals published in English. Initiated by Alexander Tilloch in 1798, in 1822 Richard Taylor became joint editor and it has been published continuously by Taylor & Francis ever since; it was the journal of choice for such luminaries as...

(Cockle 1849). The introductory papers by Cockle were recalled in the 1904 Bibliography of the Quaternion Society. Alexander Macfarlane

Alexander Macfarlane

Alexander Macfarlane was a Nova Scotia lawyer and political figure. He was a member of the Canadian Senate from 1870 to 1898. His surname also appears as McFarlane in some sources....

called the structure of coquaternion vectors an exspherical system when he was speaking at the International Congress of Mathematicians

International Congress of Mathematicians

The International Congress of Mathematicians is the largest conference for the topic of mathematics. It meets once every four years, hosted by the International Mathematical Union ....

in Paris in 1900.

The unit sphere was considered in 1910 by Hans Beck (Beck 1910: e.g., the dihedral group appears on page 419). The coquaternion structure has also been mentioned briefly in the Annals of Mathematics
Annals of Mathematics
The Annals of Mathematics is a bimonthly mathematical journal published by Princeton University and the Institute for Advanced Study. It ranks amongst the most prestigious mathematics journals in the world by criteria such as impact factor.-History:The journal began as The Analyst in 1874 and was...

(Albert 1942, Bargmann 1947).

Synonyms

Para-quaternions (Ivanov and Zamkovoy 2005, Mohaupt 2006) Manifolds with para-quaternionic structures are studied in differential geometry and string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...

. In the para-quaternionic literature k is replaced with −k.
Musean hyperbolic quaternions
Exspherical system (Macfarlane 1900)
Split-quaternions (Rosenfeld 1988)
Antiquaternions (Rosenfeld 1988)
Pseudoquaternions (Rosenfeld 1988)