
Rotor (mathematics)
Encyclopedia
A rotor is an n-blade object in geometric algebra
, which rotates another n-blade object about a fixed or translated
point
. They are normally motivated by considering an even number of reflections, which generate rotations (see also the Cartan–Dieudonné theorem). Reflections in geometric algebra are handled via (minus) sandwiching multivectors between a unit vector perpendicular to the hyperplane of reflection. Thus rotors are automatically normalised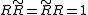 . Under a rotation generated by the rotor
. Under a rotation generated by the rotor 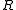 , a general multivector
, a general multivector
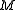 will transform double-sidedly as
will transform double-sidedly as
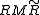 . However, as rotors can be combined and follow a group
. However, as rotors can be combined and follow a group
multiplication law, rotors themselves transform single-sidedly under further rotations. This in particular motivates the definition of spinor
in geometric algebra as an object that transforms single-sidedly — i.e. spinors are essentially unnormalised rotors.
Geometric algebra
Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
, which rotates another n-blade object about a fixed or translated
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
. They are normally motivated by considering an even number of reflections, which generate rotations (see also the Cartan–Dieudonné theorem). Reflections in geometric algebra are handled via (minus) sandwiching multivectors between a unit vector perpendicular to the hyperplane of reflection. Thus rotors are automatically normalised
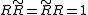 . Under a rotation generated by the rotor
. Under a rotation generated by the rotor 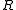 , a general multivector
, a general multivectorMultivector
In multilinear algebra, a multivector or clif is an element of the exterior algebra on a vector space, \Lambda^* V. This algebra consists of linear combinations of simple k-vectors v_1\wedge\cdots\wedge v_k."Multivector" may mean either homogeneous elements In multilinear algebra, a multivector...
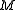 will transform double-sidedly as
will transform double-sidedly as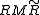 . However, as rotors can be combined and follow a group
. However, as rotors can be combined and follow a groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
multiplication law, rotors themselves transform single-sidedly under further rotations. This in particular motivates the definition of spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
in geometric algebra as an object that transforms single-sidedly — i.e. spinors are essentially unnormalised rotors.

