
Julia set
Encyclopedia
.png)
Complex dynamics
Complex dynamics is the study of dynamical systems defined by iteration of functions on complex number spaces. Complex analytic dynamics is the study of the dynamics of specifically analytic functions.-Techniques:*General** Montel's theorem...
, a topic of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Julia set and the Fatou set are two complementary sets defined from a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
. Informally, the Fatou set of the function consists of values with the property that all nearby values behave similarly under repeated iteration
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
of the function, and the Julia set consists of values such that an arbitrarily small perturbation can cause drastic changes in the sequence of iterated function values.
Thus the behavior of the function on the Fatou set is 'regular', while on the Julia set its behavior is 'chaotic
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
'.
The Julia set of a function ƒ is commonly denoted J(ƒ), and the Fatou set is denoted F(ƒ). These sets are named after the French mathematicians Gaston Julia
Gaston Julia
Gaston Maurice Julia was a French mathematician who devised the formula for the Julia set. His works were popularized by French mathematician Benoît Mandelbrot; the Julia and Mandelbrot fractals are closely related....
and Pierre Fatou
Pierre Fatou
Pierre Joseph Louis Fatou was a French mathematician working in the field of complex analytic dynamics. He entered the École Normale Supérieure in Paris in 1898 to study mathematics and graduated in 1901 when he was appointed an astronomy post in the Paris Observatory...
, whose work began the study of complex dynamics
Complex dynamics
Complex dynamics is the study of dynamical systems defined by iteration of functions on complex number spaces. Complex analytic dynamics is the study of the dynamics of specifically analytic functions.-Techniques:*General** Montel's theorem...
during the early 20th century.
Formal definition
Let be a complex rational map from the plane into itself, that is,
be a complex rational map from the plane into itself, that is, 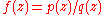 , where
, where 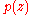 and
and 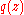 are complex polynomials. Then there are a finite number of open sets
are complex polynomials. Then there are a finite number of open sets  , that are left invariant by
, that are left invariant by 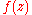 and are such that:
and are such that:-
- the union of the
 's is dense in the plane and
's is dense in the plane and  behaves in a regular and equal way on each of the sets
behaves in a regular and equal way on each of the sets  .
.
- the union of the
The last statement means that the termini of the sequences of iterations generated by the points of
 are either precisely the same set, which is then a finite cycle, or they are finite cycles of finite or annular shaped sets that are lying concentrically. In the first case the cycle is attracting, in the second it is neutral.
are either precisely the same set, which is then a finite cycle, or they are finite cycles of finite or annular shaped sets that are lying concentrically. In the first case the cycle is attracting, in the second it is neutral.These sets
 are the Fatou domains of
are the Fatou domains of  , and their union is the Fatou set
, and their union is the Fatou set  of
of 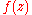 . Each of the Fatou domains contains at least one critical point of
. Each of the Fatou domains contains at least one critical point of 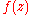 , that is, a (finite) point z satisfying
, that is, a (finite) point z satisfying  , or z = ∞, if the degree of the numerator
, or z = ∞, if the degree of the numerator 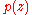 is at least two larger than the degree of the denominator
is at least two larger than the degree of the denominator 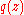 , or if
, or if 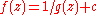 for some c and a rational function
for some c and a rational function 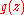 satisfying this condition.
satisfying this condition.The complement of
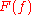 is the Julia set
is the Julia set  of
of 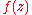 .
.  is a nowhere dense set (it is without interior points) and an uncountable set (of the same cardinality as the real numbers). Like
is a nowhere dense set (it is without interior points) and an uncountable set (of the same cardinality as the real numbers). Like  ,
, 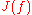 is left invariant by
is left invariant by 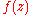 , and on this set the iteration is repelling, meaning that
, and on this set the iteration is repelling, meaning that  for all w in a neighbourhood of z (within
for all w in a neighbourhood of z (within 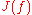 ). This means that
). This means that 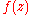 behaves chaotically on the Julia set. Although there are points in the Julia set whose sequence of iterations is finite, there are only a countable number of such points (and they make up an infinitely small part of the Julia set). The sequences generated by points outside this set behave chaotically, a phenomenon called deterministic chaos.
behaves chaotically on the Julia set. Although there are points in the Julia set whose sequence of iterations is finite, there are only a countable number of such points (and they make up an infinitely small part of the Julia set). The sequences generated by points outside this set behave chaotically, a phenomenon called deterministic chaos.There has been extensive research on the Fatou set and Julia set of iterated rational functions, known as rational maps. For example, it is known that the Fatou set of a rational map has either 0,1,2 or infinitely many components. Each component of the Fatou set of a rational map can be classified into one of four different classes
Classification of Fatou components
In mathematics, if f = P/Q is a rational function defined in the extended complex plane, and ifthen for a periodic component U of the Fatou set, exactly one of the following holds:# U contains an attracting periodic point# U is parabolic...
.
Equivalent descriptions of the Julia set
-
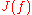 is the smallest closed set containing at least three points which is completely invariant under
is the smallest closed set containing at least three points which is completely invariant under  .
. -
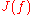 is the closureClosure (mathematics)In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
is the closureClosure (mathematics)In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
of the set of repelling periodic pointPeriodic pointIn mathematics, in the study of iterated functions and dynamical systems, a periodic point of a function is a point which the system returns to after a certain number of function iterations or a certain amount of time.- Iterated functions :...
s. - For all but at most two points
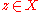 , the Julia set is the set of limit points of the full backwards orbit
, the Julia set is the set of limit points of the full backwards orbit 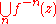 . (This suggests a simple algorithm for plotting Julia sets, see below.)
. (This suggests a simple algorithm for plotting Julia sets, see below.) - If
 is an entire functionEntire functionIn complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
is an entire functionEntire functionIn complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
- in particular, when is a polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
is a polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
, then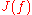 is the boundaryBoundary (topology)In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
is the boundaryBoundary (topology)In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of the set of points which converge to infinity under iteration. - If
 is a polynomial, then
is a polynomial, then 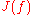 is the boundary of the filled Julia setFilled Julia setThe filled-in Julia set \ K of a polynomial \ f is a Julia set and its interior.-Formal definition:The filled-in Julia set \ K of a polynomial \ f is defined as the set of all points z\, of dynamical plane that have bounded orbit with respect to \ f...
is the boundary of the filled Julia setFilled Julia setThe filled-in Julia set \ K of a polynomial \ f is a Julia set and its interior.-Formal definition:The filled-in Julia set \ K of a polynomial \ f is defined as the set of all points z\, of dynamical plane that have bounded orbit with respect to \ f...
; that is, those points whose orbits under iterations of remain bounded.
remain bounded.
Properties of the Julia set and Fatou set
The Julia set and the Fatou set of are both completely invariant
are both completely invariantInvariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
under iterations of the holomorphic function
 , i.e.
, i.e.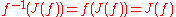
and
 .
.Examples
For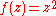 the Julia set is the unit circle and on this the iteration is given by doubling of angles (an operation that is chaotic on the non-rational points). There are two Fatou domains: the interior and the exterior of the circle, with iteration towards 0 and ∞, respectively.
the Julia set is the unit circle and on this the iteration is given by doubling of angles (an operation that is chaotic on the non-rational points). There are two Fatou domains: the interior and the exterior of the circle, with iteration towards 0 and ∞, respectively.For
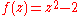 the Julia set is the line segment between -2 and 2, and the iteration corresponds to
the Julia set is the line segment between -2 and 2, and the iteration corresponds to 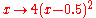 in the unit interval. This can be used as a method for generating pseudorandom numbers
in the unit interval. This can be used as a method for generating pseudorandom numbersPseudorandom number generator
A pseudorandom number generator , also known as a deterministic random bit generator , is an algorithm for generating a sequence of numbers that approximates the properties of random numbers...
. There is one Fatou domain: the points not on the line segment iterate towards ∞.
These two functions are of the form
 , where c is a complex number. For such an iteration the Julia set is not in general a simple curve, but is a fractal, and for some values of c it can take surprising shapes. See the pictures below.
, where c is a complex number. For such an iteration the Julia set is not in general a simple curve, but is a fractal, and for some values of c it can take surprising shapes. See the pictures below.
 we can say beforehand that the Julia set is a fractal and not a simple curve. This is because of the following main theorem on the iterations of a rational function:
we can say beforehand that the Julia set is a fractal and not a simple curve. This is because of the following main theorem on the iterations of a rational function:Each of the Fatou domains has the same boundary, which consequently is the Julia set
This means that each point of the Julia set is a point of accumulation for each of the Fatou domains. Therefore, if there are more than two Fatou domains, each point of the Julia set must have points of more than two different open sets infinitely close, and this means that the Julia set cannot be a simple curve. This phenomenon happens, for instance, when
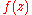 is the Newton iteration for solving the equation
is the Newton iteration for solving the equation 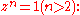
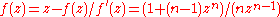 . The image on the right shows the case n = 3.
. The image on the right shows the case n = 3.Quadratic polynomials
A very popular complex dynamical system is given by the family of quadratic polynomialsComplex quadratic polynomial
A complex quadratic polynomial is a quadratic polynomial whose coefficients are complex numbers.-Forms:When the quadratic polynomial has only one variable , one can distinguish its 4 main forms:...
, a special case of rational maps
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
. The quadratic polynomials
Complex quadratic polynomial
A complex quadratic polynomial is a quadratic polynomial whose coefficients are complex numbers.-Forms:When the quadratic polynomial has only one variable , one can distinguish its 4 main forms:...
can be expressed as
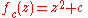
where
 is a complex parameter.
is a complex parameter.The parameter plane of quadratic polynomials - that is, the plane of possible
 -values - gives rise to the famous Mandelbrot set
-values - gives rise to the famous Mandelbrot setMandelbrot set
The Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
. Indeed, the Mandelbrot set is defined as the set of all
 such that
such that  is connected. For parameters outside the Mandelbrot set, the Julia set is a Cantor set
is connected. For parameters outside the Mandelbrot set, the Julia set is a Cantor setCantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
: in this case it is sometimes referred to as Fatou dust.
In many cases, the Julia set of
 looks like the Mandelbrot set in sufficiently small neighborhoods of
looks like the Mandelbrot set in sufficiently small neighborhoods of  . This is true, in particular, for so-called 'Misiurewicz' parameters
. This is true, in particular, for so-called 'Misiurewicz' parametersMisiurewicz point
A Misiurewicz point is a parameter in the Mandelbrot set for which the critical point is strictly preperiodic . By analogy, the term Misiurewicz point is also used for parameters in a Multibrot set where the unique critical point is strictly preperiodic...
, i.e. parameters
 for which the critical point is pre-periodic. For instance:
for which the critical point is pre-periodic. For instance:
- At
 , the shorter, front toe of the forefoot, the Julia set looks like a branched lightning bolt.
, the shorter, front toe of the forefoot, the Julia set looks like a branched lightning bolt. - At
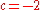 , the tip of the long spiky tail, the Julia set is a straight line segment.
, the tip of the long spiky tail, the Julia set is a straight line segment.
In other words the Julia sets
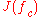 are locally similar around Misiurewicz point
are locally similar around Misiurewicz pointMisiurewicz point
A Misiurewicz point is a parameter in the Mandelbrot set for which the critical point is strictly preperiodic . By analogy, the term Misiurewicz point is also used for parameters in a Multibrot set where the unique critical point is strictly preperiodic...
s.
Generalizations
The definition of Julia and Fatou sets easily carries over to the case of certain maps whose image contains their domain; most notably transcendental meromorphic functionsMeromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
and Adam Epstein's finite-type maps.
Julia sets are also commonly defined in the study of dynamics in several complex variables.
The potential function and the real iteration number
The Julia set for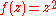 is the unit circle, and on the outer Fatou domain, the potential function
is the unit circle, and on the outer Fatou domain, the potential function 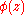 is defined by
is defined by 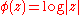 . The equipotential lines for this function are concentric circles. As
. The equipotential lines for this function are concentric circles. As  we have
we have 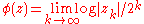 , where
, where  is the sequence of iteration generated by z. For the more general iteration
is the sequence of iteration generated by z. For the more general iteration 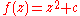 , it has been proved that if the Julia set is connected (that is, if c belongs to the (usual) Mandelbrot set), then there exist a biholomorphic map
, it has been proved that if the Julia set is connected (that is, if c belongs to the (usual) Mandelbrot set), then there exist a biholomorphic map 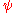 between the outer Fatou domain and the outer of the unit circle such that
between the outer Fatou domain and the outer of the unit circle such that 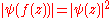 . This means that the potential function on the outer Fatou domain defined by this correspondence is given by:
. This means that the potential function on the outer Fatou domain defined by this correspondence is given by: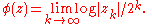
This formula has meaning also if the Julia set is not connected, so that we for all c can define the potential function on the Fatou domain containing ∞ by this formula. For a general rational function
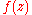 such that ∞ is a critical point and a fixed point, that is, such that the degree m of the numerator is at least two larger than the degree n of the denominator, we define the potential function on the Fatou domain containing ∞ by:
such that ∞ is a critical point and a fixed point, that is, such that the degree m of the numerator is at least two larger than the degree n of the denominator, we define the potential function on the Fatou domain containing ∞ by: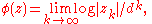
where d = m - n is the degree of the rational function.
If N is a very large number (e.g. 10100), and if k is the first iteration number such that
 , we have that
, we have that 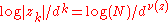 , for some real number
, for some real number 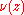 , which should be regarded as the real iteration number, and we have that:
, which should be regarded as the real iteration number, and we have that:
where the last number is in the interval
For iteration towards a finite attracting cycle of order r, we have that if z* is a point of the cycle, then
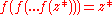 (the r-fold composition), and the number
(the r-fold composition), and the number 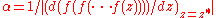 (> 1) is the attraction of the cycle. If w is a point very near z* and w is w iterated r times, we have that
(> 1) is the attraction of the cycle. If w is a point very near z* and w is w iterated r times, we have that 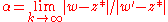 . Therefore the number
. Therefore the number 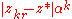 is almost independent of k. We define the potential function on the Fatou domain by:
is almost independent of k. We define the potential function on the Fatou domain by: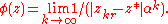
If
 is a very small number and k is the first iteration number such that
is a very small number and k is the first iteration number such that 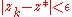 , we have that
, we have that 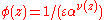 for some real number
for some real number 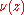 , which should be regarded as the real iteration number, and we have that:
, which should be regarded as the real iteration number, and we have that: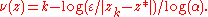
If the attraction is ∞, meaning that the cycle is super-attracting, meaning again that one of the points of the cycle is a critical point, we must replace
 by
by 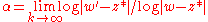 (where w is w iterated r times) and the formula for
(where w is w iterated r times) and the formula for  by:
by:
And now the real iteration number is given by:

For the colouring we must have a cyclic scale of colours (constructed mathematically, for instance) and containing H colours numbered from 0 to H-1 (H = 500, for instance). We multiply the real number
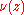 by a fixed real number determining the density of the colours in the picture, and take the integral part of this number modulo H.
by a fixed real number determining the density of the colours in the picture, and take the integral part of this number modulo H.The definition of the potential function and our way of colouring presuppose that the cycle is attracting, that is, not neutral. If the cycle is neutral, we cannot colour the Fatou domain in a natural way. As the terminus of the iteration is a revolving movement, we can, for instance, colour by the minimum distance from the cycle left fixed by the iteration.
Field lines
In each Fatou domain (that is not neutral) there are two systems of lines orthogonal to each other: the equipotential lines (for the potential function or the real iteration number) and the field lines.If we colour the Fatou domain according to the iteration number (and not the real iteration number), the bands of iteration show the course of the equipotential lines. If the iteration is towards ∞ (as is the case with the outer Fatou domain for the usual iteration
 ), we can easily show the course of the field lines, namely by altering the colour according as the last point in the sequence of iteration is above or below the x-axis (first picture), but in this case (more precisely: when the Fatou domain is super-attracting) we cannot draw the field lines coherently - at least not by the method we describe here. In this case a field line is also called an external ray
), we can easily show the course of the field lines, namely by altering the colour according as the last point in the sequence of iteration is above or below the x-axis (first picture), but in this case (more precisely: when the Fatou domain is super-attracting) we cannot draw the field lines coherently - at least not by the method we describe here. In this case a field line is also called an external rayExternal ray
An external ray is a curve that runs from infinity toward a Julia or Mandelbrot set.This curve is only sometimes a half-line but is called ray because it is image of ray....
.
Let z be a point in the attracting Fatou domain. If we iterate z a large number of times, the terminus of the sequence of iteration is a finite cycle C, and the Fatou domain is (by definition) the set of points whose sequence of iteration converges towards C. The field lines issue from the points of C and from the (infinite number of) points that iterate into a point of C. And they end on the Julia set in points that are non-chaotic (that is, generating a finite cycle). Let r be the order of the cycle C (its number of points) and let z* be a point in C. We have
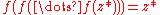 (the r-fold composition), and we define the complex number
(the r-fold composition), and we define the complex number  by
by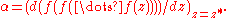
If the points of C are
 ,
,  is the product of the r numbers
is the product of the r numbers 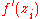 . The real number 1/
. The real number 1/ is the attraction of the cycle, and our assumption that the cycle is neither neutral nor super-attracting, means that 1 < 1/|α| < ∞. The point z* is a fixed point for
is the attraction of the cycle, and our assumption that the cycle is neither neutral nor super-attracting, means that 1 < 1/|α| < ∞. The point z* is a fixed point for  , and near this point the map
, and near this point the map  has (in connection with field lines) character of a rotation with the argument
has (in connection with field lines) character of a rotation with the argument 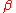 of
of  (that is,
(that is, 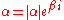 ).
).In order to colour the Fatou domain, we have chosen a small number
 and set the sequences of iteration
and set the sequences of iteration 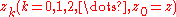 to stop when
to stop when  , and we colour the point z according to the number k (or the real iteration number, if we prefer a smooth colouring). If we choose a direction from z* given by an angle
, and we colour the point z according to the number k (or the real iteration number, if we prefer a smooth colouring). If we choose a direction from z* given by an angle 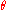 , the field line issuing from z* in this direction consists of the points z such that the argument
, the field line issuing from z* in this direction consists of the points z such that the argument  of the number
of the number 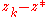 satisfies the condition that
satisfies the condition that
For if we pass an iteration band in the direction of the field lines (and away from the cycle), the iteration number k is increased by 1 and the number
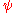 is increased by
is increased by 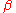 , therefore the number
, therefore the number  is constant along the field line.
is constant along the field line.A colouring of the field lines of the Fatou domain means that we colour the spaces between pairs of field lines: we choose a number of regularly situated directions issuing from z*, and in each of these directions we choose two directions around this direction. As it can happen that the two field lines of a pair do not end in the same point of the Julia set, our coloured field lines can ramify (endlessly) in their way towards the Julia set. We can colour on the basis of the distance to the centre line of the field line, and we can mix this colouring with the usual colouring. Such pictures can be very decorative (second picture).
A coloured field line (the domain between two field lines) is divided up by the iteration bands, and such a part can be put into a one-to-one correspondence with the unit square: the one coordinate is (calculated from) the distance from one of the bounding field lines, the other is (calculated from) the distance from the inner of the bounding iteration bands (this number is the non-integral part of the real iteration number). Therefore we can put pictures into the field lines (third picture).
Distance estimation
As a Julia set is infinitely thin we cannot draw it effectively by backwards iteration from the pixels. It will appear fragmented because of the impracticality of examining infinitely many startpoints. Since the iteration count changes vigorously near the Julia set, a partial solution is to imply the outline of the set from the nearest color contours, but the set will tend to look muddy.A better way to draw the Julia set in black and white is to estimate the distance of pixels from the set and to color every pixel whose center is close to the set. The formula for the distance estimation is derived from the formula for the potential function
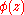 . When the equipotential lines for
. When the equipotential lines for 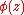 lie close, the number
lie close, the number  is large, and conversely, therefore the equipotential lines for the function
is large, and conversely, therefore the equipotential lines for the function 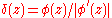 should lie approximately regularly. It has been proven that the value found by this formula (up to a constant factor) converges towards the true distance for z converging towards the Julia set.
should lie approximately regularly. It has been proven that the value found by this formula (up to a constant factor) converges towards the true distance for z converging towards the Julia set.We assume that
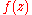 is rational, that is,
is rational, that is, 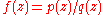 where
where  and
and 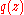 are complex polynomials of degrees m and n, respectively, and we have to find the derivative of the above expressions for
are complex polynomials of degrees m and n, respectively, and we have to find the derivative of the above expressions for 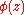 . And as it is only
. And as it is only 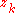 that varies, we must calculate the derivative
that varies, we must calculate the derivative 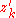 of
of 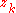 with respect to z. But as
with respect to z. But as 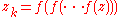 (the k-fold composition),
(the k-fold composition), 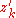 is the product of the numbers
is the product of the numbers 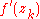 , and this sequence can be calculated recursively by
, and this sequence can be calculated recursively by 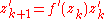 , starting with
, starting with 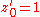 (before the calculation of the next iteration
(before the calculation of the next iteration 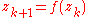 ).
).For iteration towards ∞ (more precisely when m ≥ n + 2, so that ∞ is a super-attracting fixed point), we have
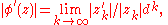
(d = m − n) and consequently:

For iteration towards a finite attracting cycle (that is not super-attracting) containing the point z* and having order r, we have

and consequently:
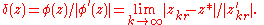
For a super-attracting cycle, the formula is:
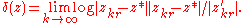
We calculate this number when the iteration stops. Note that the distance estimation is independent of the attraction of the cycle. This means that it has meaning for transcendental functions of "degree infinity" (e.g. sin(z) and tan(z)).
Besides drawing of the boundary, the distance function can be introduced as a 3rd dimension to create a solid fractal landscape.
Using backwards (inverse) iteration (IIM)
.gif)

 we know to be in the Julia set, such as a repelling periodic point, and compute all pre-images of
we know to be in the Julia set, such as a repelling periodic point, and compute all pre-images of  under some high iterate
under some high iterate  of
of  .
.Unfortunately, as the number of iterated pre-images grows exponentially, this is not feasible computationally. However, we can adjust this method, in a similar way as the "random game" method for
iterated function system
Iterated function system
In mathematics, iterated function systems or IFSs are a method of constructing fractals; the resulting constructions are always self-similar....
s. That is, in each step, we choose at random one of the inverse images of
 .
.For example, for the quadratic polynomial
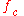 , the backwards iteration is described by
, the backwards iteration is described by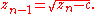
At each step, one of the two square roots is selected at random.
Note that certain parts of the Julia set are quite difficult to access with the reverse Julia algorithm. For this reason, one must modify IIM/J ( it is called MIIM/J) or use other methods to produce better images.
See also
- Limit setLimit setIn mathematics, especially in the study of dynamical systems, a limit set is the state a dynamical system reaches after an infinite amount of time has passed, by either going forward or backwards in time...
- Stable and unstable sets
- No wandering domain theoremNo wandering domain theoremIn mathematics, the no-wandering-domain theorem is a result on dynamical systems, proven by Dennis Sullivan in 1985.The theorem states that a rational map f : Ĉ → Ĉ with deg ≥ 2 does not have a wandering domain, where Ĉ denotes the Riemann sphere...
- Fatou componentsClassification of Fatou componentsIn mathematics, if f = P/Q is a rational function defined in the extended complex plane, and ifthen for a periodic component U of the Fatou set, exactly one of the following holds:# U contains an attracting periodic point# U is parabolic...
- Chaos theoryChaos theoryChaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
External links
- Julia Set Fractal (2D), Paul Burke
- Julia Sets, Jamie Sawyer
- Julia Jewels: An Exploration of Julia Sets, Michael McGoodwin
- Crop circle Julia Set, Lucy Pringle
- Interactive Julia Set Applet, Josh Greig
- Julia and Mandelbrot Set Explorer, David E. Joyce
- A simple program to generate Julia sets (Windows, 370 kb)
- A collection of applets one of which can render Julia sets via Iterated Function Systems.
- Julia meets HTML5 Google Labs' HTML5 Fractal generator on your browser
- Julia GNU R Package to generate Julia or Mandelbrot set at a given region and resolution.
- Julia sets A visual explanation of Julia Sets.

