Homomorphism
Encyclopedia
In abstract algebra
, a homomorphism is a structure-preserving map
between two algebraic structure
s (such as group
s, ring
s, or vector space
s). The word homomorphism comes from the Greek language
: ὁμός (homos) meaning "same" and μορφή (morphe) meaning "shape".
under consideration. Particular definitions of homomorphism include the following:
The common theme is that a homomorphism is a function
between two algebraic objects that respects the algebraic structure.
For example, a group is an algebraic object consisting of a set together with a single binary operation
, satisfying certain axioms. If G and H are groups, a homomorphism from G to H is a function ƒ: G → H such that

for any elements g1, g2 ∈ G, where * denotes the operation in G and *' denotes the operation in H.
When an algebraic structure includes more than one operation, homomorphisms are required to preserve each operation. For example, a ring possesses both addition and multiplication, and a homomorphism between two rings is a function such that
for any elements r and s of the domain
ring.
The notion of a homomorphism can be given a formal definition in the context of universal algebra
, a field which studies ideas common to all algebraic structures. In this setting, a homomorphism ƒ: A → B is a function between two algebraic structures of the same type such that
for each n-ary operation μ and for all elements a1,...,an ∈ A.
s are a ring
, having both addition and multiplication. The set of all 2 × 2 matrices
is also a ring, under matrix addition
and matrix multiplication
. If we define a function between these rings as follows:
where r is a real number. Then ƒ is a homomorphism of rings, since ƒ preserves both addition:
and multiplication:
For another example, the nonzero complex number
s form a group
under the operation of multiplication, as do the nonzero real numbers. (Zero must be excluded from both groups since it does not have a multiplicative inverse
, which is required for elements of a group.) Define a function ƒ from the nonzero complex numbers to the nonzero real numbers by
That is, ƒ(z) is the absolute value
(or modulus) of the complex number z. Then ƒ is a homomorphism of groups, since it preserves multiplication:
Note that ƒ cannot be extended to a homomorphism of rings (from the complex numbers to the real numbers), since it does not preserve addition:
that generate interesting structure or properties on the set, function
s which preserve the operations are especially important. These functions are known as homomorphisms.
For example, consider the natural number
s with addition as the operation. A function which preserves addition should have this property: f(a + b) = f(a) + f(b). For example, f(x) = 3x is one such homomorphism, since f(a + b) = 3(a + b) = 3a + 3b = f(a) + f(b). Note that this homomorphism maps the natural numbers back into themselves.
Homomorphisms do not have to map between sets which have the same operations. For example, operation-preserving functions exist between the set of real numbers with addition and the set of positive real numbers with multiplication. A function which preserves operation should have this property: f(a + b) = f(a) * f(b), since addition is the operation in the first set and multiplication is the operation in the second. Given the laws of exponents, f(x) = ex satisfies this condition : 2 + 3 = 5 translates into e2 * e3 = e5.
If we are considering multiple operations on a set, then all operations must be preserved for a function to be considered as a homomorphism. Even though the set may be the same, the same function might be a homomorphism, say, in group theory
(sets with a single operation) but not in ring theory
(sets with two related operations), because it fails to preserve the additional operation that ring theory considers.
s, the following specific kinds of morphisms defined in any category are defined for homomorphisms as well. However, the definitions in category theory
are somewhat technical. In the important special case of module homomorphisms, and for some other classes of homomorphisms, there are much simpler descriptions, as follows:
These descriptions may be used in order to derive several interesting properties. For instance, since a function is bijective if and only if it is both injective and surjective, a module homomorphism is an isomorphism if and only if it is both a monomorphism and an epimorphism.
For endomorphisms and automorphisms, the descriptions above coincide with the category theoretic definitions; the first three descriptions do not. For instance, the precise definition for a homomorphism f to be iso is not only that it is bijective, and thus has an inverse f-1, but also that this inverse is a homomorphism, too. This has the important consequence that two objects are completely indistinguishable as far as the structure in question is concerned, if there is an isomorphism between them. Two such objects are said to be isomorphic.
Actually, in the algebraic setting (at least within the context of universal algebra
) this extra condition on isomorphisms is automatically satisfied. However, the same is not true for epimorphisms; for instance, the inclusion of Z
as a (unitary) subring of Q
is not surjective, but an epimorphic ring homomorphism
. This inclusion thus also is an example of a ring homomorphism which is both mono and epi, but not iso.
~ on X by a ~ b if and only if f(a) = f(b). The relation ~ is called the kernel of f. It is a congruence relation
on X. The quotient set X/~ can then be given an object-structure in a natural way, i.e. [x] * [y] = [x * y]. In that case the image of X in Y under the homomorphism f is necessarily isomorphic to X/~; this fact is one of the isomorphism theorem
s. Note in some cases (e.g. group
s or rings), a single equivalence class K suffices to specify the structure of the quotient; so we can write it X/K. (X/K is usually read as "X mod
K".) Also in these cases, it is K, rather than ~, that is called the kernel
of f (cf. normal subgroup
).
, the notion of an algebraic structure is generalized to structures involving both operations and relations. Let L be a signature consisting of function and relation symbols, and A, B be two L-structures. Then a homomorphism from A to B is a mapping h from the domain of A to the domain of B such that
In the special case with just one binary relation, we obtain the notion of a graph homomorphism
.
s (although within this context, often they are briefly referred to as morphisms). Given alphabets and
and  , a function h :
, a function h :  →
→  such that
such that  for all u and v in
for all u and v in  is called a homomorphism (or simply morphism) on
is called a homomorphism (or simply morphism) on  . Let e denote the empty word. If h is a homomorphism on
. Let e denote the empty word. If h is a homomorphism on  and
and  for all
for all  in
in  , then h is called an e-free homomorphism.
, then h is called an e-free homomorphism.
This type of homomorphism can be thought of as (and is equivalent to) a monoid homomorphism where the set of all words over a finite alphabet
the set of all words over a finite alphabet  is a monoid (in fact it is the free monoid on
is a monoid (in fact it is the free monoid on  ) with operation concatenation and the empty word as the identity.
) with operation concatenation and the empty word as the identity.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a homomorphism is a structure-preserving map
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
between two algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s (such as group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s, ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
s, or vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s). The word homomorphism comes from the Greek language
Greek language
Greek is an independent branch of the Indo-European family of languages. Native to the southern Balkans, it has the longest documented history of any Indo-European language, spanning 34 centuries of written records. Its writing system has been the Greek alphabet for the majority of its history;...
: ὁμός (homos) meaning "same" and μορφή (morphe) meaning "shape".
Definition
The definition of homomorphism depends on the type of algebraic structureAlgebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
under consideration. Particular definitions of homomorphism include the following:
- A group homomorphismGroup homomorphismIn mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
is a homomorphism between two groupsGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. - A ring homomorphismRing homomorphismIn ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
is a homomorphism between two ringsRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
. - A linear map is a homomorphism between two vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s. - An algebra homomorphismAlgebra homomorphismA homomorphism between two algebras, A and B, over a field K, is a map F:A\rightarrow B such that for all k in K and x,y in A,* F = kF* F = F + F...
is a homomorphism between two algebrasAlgebra over a fieldIn mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
. - A functorFunctorIn category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
is a homomorphism between two categoriesCategory (mathematics)In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
.
The common theme is that a homomorphism is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
between two algebraic objects that respects the algebraic structure.
For example, a group is an algebraic object consisting of a set together with a single binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
, satisfying certain axioms. If G and H are groups, a homomorphism from G to H is a function ƒ: G → H such that

for any elements g1, g2 ∈ G, where * denotes the operation in G and *' denotes the operation in H.
When an algebraic structure includes more than one operation, homomorphisms are required to preserve each operation. For example, a ring possesses both addition and multiplication, and a homomorphism between two rings is a function such that

for any elements r and s of the domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
ring.
The notion of a homomorphism can be given a formal definition in the context of universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
, a field which studies ideas common to all algebraic structures. In this setting, a homomorphism ƒ: A → B is a function between two algebraic structures of the same type such that

for each n-ary operation μ and for all elements a1,...,an ∈ A.
Basic examples
The real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s are a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, having both addition and multiplication. The set of all 2 × 2 matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
is also a ring, under matrix addition
Matrix addition
In mathematics, matrix addition is the operation of adding two matrices by adding the corresponding entries together. However, there are other operations which could also be considered as a kind of addition for matrices, the direct sum and the Kronecker sum....
and matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
. If we define a function between these rings as follows:

where r is a real number. Then ƒ is a homomorphism of rings, since ƒ preserves both addition:

and multiplication:

For another example, the nonzero complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s form a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
under the operation of multiplication, as do the nonzero real numbers. (Zero must be excluded from both groups since it does not have a multiplicative inverse
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
, which is required for elements of a group.) Define a function ƒ from the nonzero complex numbers to the nonzero real numbers by

That is, ƒ(z) is the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
(or modulus) of the complex number z. Then ƒ is a homomorphism of groups, since it preserves multiplication:

Note that ƒ cannot be extended to a homomorphism of rings (from the complex numbers to the real numbers), since it does not preserve addition:

Informal discussion
Because abstract algebra studies sets endowed with operationsOperation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
that generate interesting structure or properties on the set, function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s which preserve the operations are especially important. These functions are known as homomorphisms.
For example, consider the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s with addition as the operation. A function which preserves addition should have this property: f(a + b) = f(a) + f(b). For example, f(x) = 3x is one such homomorphism, since f(a + b) = 3(a + b) = 3a + 3b = f(a) + f(b). Note that this homomorphism maps the natural numbers back into themselves.
Homomorphisms do not have to map between sets which have the same operations. For example, operation-preserving functions exist between the set of real numbers with addition and the set of positive real numbers with multiplication. A function which preserves operation should have this property: f(a + b) = f(a) * f(b), since addition is the operation in the first set and multiplication is the operation in the second. Given the laws of exponents, f(x) = ex satisfies this condition : 2 + 3 = 5 translates into e2 * e3 = e5.
If we are considering multiple operations on a set, then all operations must be preserved for a function to be considered as a homomorphism. Even though the set may be the same, the same function might be a homomorphism, say, in group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
(sets with a single operation) but not in ring theory
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
(sets with two related operations), because it fails to preserve the additional operation that ring theory considers.
Relation to category theory
Since homomorphisms are morphismMorphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s, the following specific kinds of morphisms defined in any category are defined for homomorphisms as well. However, the definitions in category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
are somewhat technical. In the important special case of module homomorphisms, and for some other classes of homomorphisms, there are much simpler descriptions, as follows:
- An isomorphismIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
is a bijective homomorphism.
- An epimorphismEpimorphismIn category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
(sometimes called a coverCover (algebra)In abstract algebra, a cover is one instance of some mathematical structure mapping onto another instance, such as a group covering a subgroup. This should not be confused with the concept of a cover in topology....
) is a surjective homomorphism.
- A monomorphismMonomorphismIn the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
(sometimes called an embeddingEmbeddingIn mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
or extension) is an injective homomorphism.
- An endomorphismEndomorphismIn mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
is a homomorphism from an object to itself.
- An automorphismAutomorphismIn mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
is an endomorphism which is also an isomorphism, i.e., an isomorphism from an object to itself.
These descriptions may be used in order to derive several interesting properties. For instance, since a function is bijective if and only if it is both injective and surjective, a module homomorphism is an isomorphism if and only if it is both a monomorphism and an epimorphism.
For endomorphisms and automorphisms, the descriptions above coincide with the category theoretic definitions; the first three descriptions do not. For instance, the precise definition for a homomorphism f to be iso is not only that it is bijective, and thus has an inverse f-1, but also that this inverse is a homomorphism, too. This has the important consequence that two objects are completely indistinguishable as far as the structure in question is concerned, if there is an isomorphism between them. Two such objects are said to be isomorphic.
Actually, in the algebraic setting (at least within the context of universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
) this extra condition on isomorphisms is automatically satisfied. However, the same is not true for epimorphisms; for instance, the inclusion of Z
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
as a (unitary) subring of Q
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
is not surjective, but an epimorphic ring homomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
. This inclusion thus also is an example of a ring homomorphism which is both mono and epi, but not iso.
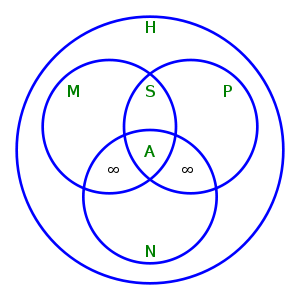
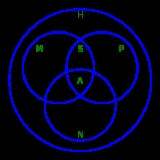
- Relationships between different kinds of module homomorphisms.
H = set of Homomorphisms, M = set of Monomorphisms,
P = set of ePimorphisms, S = set of iSomorphisms,
N = set of eNdomorphisms, A = set of Automorphisms.
Notice that: M ∩ P = S, S ∩ N = A,
(M ∩ N) \ A and (P ∩ N) \ A contain only homomorphisms from some infinite modules to themselves.
Kernel of a homomorphism
Any homomorphism f : X → Y defines an equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
~ on X by a ~ b if and only if f(a) = f(b). The relation ~ is called the kernel of f. It is a congruence relation
Congruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
on X. The quotient set X/~ can then be given an object-structure in a natural way, i.e. [x] * [y] = [x * y]. In that case the image of X in Y under the homomorphism f is necessarily isomorphic to X/~; this fact is one of the isomorphism theorem
Isomorphism theorem
In mathematics, specifically abstract algebra, the isomorphism theorems are three theorems that describe the relationship between quotients, homomorphisms, and subobjects. Versions of the theorems exist for groups, rings, vector spaces, modules, Lie algebras, and various other algebraic structures...
s. Note in some cases (e.g. group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s or rings), a single equivalence class K suffices to specify the structure of the quotient; so we can write it X/K. (X/K is usually read as "X mod
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
K".) Also in these cases, it is K, rather than ~, that is called the kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of f (cf. normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
).
Homomorphisms of relational structures
In model theoryModel theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, the notion of an algebraic structure is generalized to structures involving both operations and relations. Let L be a signature consisting of function and relation symbols, and A, B be two L-structures. Then a homomorphism from A to B is a mapping h from the domain of A to the domain of B such that
- h(FA(a1,…,an)) = FB(h(a1),…,h(an)) for each n-ary function symbol F in L,
- RA(a1,…,an) implies RB(h(a1),…,h(an)) for each n-ary relation symbol R in L.
In the special case with just one binary relation, we obtain the notion of a graph homomorphism
Graph homomorphism
In the mathematical field of graph theory a graph homomorphism is a mapping between two graphs that respects their structure. More concretely it maps adjacent vertices to adjacent vertices.-Definitions:...
.
Homomorphisms and e-free homomorphisms in formal language theory
Homomorphisms are also used in the study of formal languageFormal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
s (although within this context, often they are briefly referred to as morphisms). Given alphabets
 and
and  , a function h :
, a function h :  →
→  such that
such that  for all u and v in
for all u and v in  is called a homomorphism (or simply morphism) on
is called a homomorphism (or simply morphism) on  . Let e denote the empty word. If h is a homomorphism on
. Let e denote the empty word. If h is a homomorphism on  and
and  for all
for all  in
in  , then h is called an e-free homomorphism.
, then h is called an e-free homomorphism.This type of homomorphism can be thought of as (and is equivalent to) a monoid homomorphism where
 the set of all words over a finite alphabet
the set of all words over a finite alphabet  is a monoid (in fact it is the free monoid on
is a monoid (in fact it is the free monoid on  ) with operation concatenation and the empty word as the identity.
) with operation concatenation and the empty word as the identity.See also
- continuous functionContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
- diffeomorphismDiffeomorphismIn mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
- homomorphic encryptionHomomorphic encryptionHomomorphic encryption is a form of encryption where a specific algebraic operation performed on the plaintext is equivalent to another algebraic operation performed on the ciphertext. Depending on one's viewpoint, this can be seen as either a positive or negative attribute of the cryptosystem....
- homomorphic secret sharingHomomorphic secret sharingIn cryptography, homomorphic secret sharing is a type of secret sharing algorithm in which the secret is encrypted via homomorphic encryption. A homomorphism is a transformation from one type of algebraic structure into another so that the structure is preserved...
– a simplistic decentralized voting protocol - morphismMorphismIn mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...

