Quaternion group - AbsoluteAstronomy.com

Group theory

In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...

, the quaternion group is a non-abelian

Nonabelian group

In mathematics, a non-abelian group, also sometimes called a non-commutative group, is a group in which there are at least two elements a and b of G such that a * b ≠ b * a...

group

Group (mathematics)

In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...

of order eight, isomorphic to a certain eight-element subset of the quaternion

Quaternion

In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...

s under multiplication. It is often denoted by Q or Q₈, and is given by the group presentation

Presentation of a group

In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...

where 1 is the identity element and −1 commutes

Commutativity

In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...

with the other elements of the group.

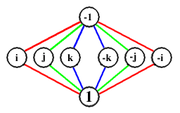
Cayley graph

The Q₈ group has the same order as the Dihedral group

Dihedral group

In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...

, D₄, but a different structure, as shown by their Cayley graphs:

Cayley graph
Cayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
Q₈ The red arrows represent multiplication on the right by i, and the green arrows represent multiplication on the right by j.	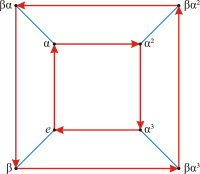D₄ Dihedral group Dihedral group In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...

Cayley table

The Cayley table

Cayley table

A Cayley table, after the 19th century British mathematician Arthur Cayley, describes the structure of a finite group by arranging all the possible products of all the group's elements in a square table reminiscent of an addition or multiplication table...

(multiplication table) for Q is given by:

	1	−1	i	−i	j	−j	k	−k
1	1	−1	i	−i	j	−j	k	−k
−1	−1	1	−i	i	−j	j	−k	k
i	i	−i	−1	1	k	−k	−j	j
−i	−i	i	1	−1	−k	k	j	−j
j	j	−j	−k	k	−1	1	i	−i
−j	−j	j	k	−k	1	−1	−i	i
k	k	−k	j	−j	−i	i	−1	1
−k	−k	k	−j	j	i	−i	1	−1

The multiplication of pairs of elements from the subset {±i, ±j, ±k} works like the cross product

Cross product

In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...

of unit vectors in three-dimensional Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

Properties

The quaternion group has the unusual property of being Hamiltonian

Hamiltonian group

In group theory, a Dedekind group is a group G such that every subgroup of G is normal.All abelian groups are Dedekind groups.A non-abelian Dedekind group is called a Hamiltonian group....

: every subgroup

Subgroup

In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...

of Q is a normal subgroup

Normal subgroup

In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....

, but the group is non-abelian. Every Hamiltonian group contains a copy of Q.

In abstract algebra

Abstract algebra

Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...

, one can construct a real four-dimensional vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

with basis {1, i, j, k} and turn it into an associative algebra

Associative algebra

In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...

by using the above multiplication table and distributivity

Distributivity

In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...

. The result is a skew field called the quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...

s. Note that this is not quite the same as the group algebra

Group algebra

In mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...

on Q (which would be eight-dimensional). Conversely, one can start with the quaternions and define the quaternion group as the multiplicative subgroup consisting of the eight elements {1, −1, i, −i, j, −j, k, −k}. The complex four-dimensional vector space on the same basis is called the algebra of biquaternions.

Note that i, j, and k all have order four in Q and any two of them generate the entire group. Another presentation

Presentation of a group

of Q demonstrating this is:

One may take, for instance, i = x, j = y and k = xy.

The center and the commutator subgroup

Commutator subgroup

In mathematics, more specifically in abstract algebra, the commutator subgroup or derived subgroup of a group is the subgroup generated by all the commutators of the group....

of Q is the subgroup {±1}. The factor group Q/{±1} is isomorphic to the Klein four-group

Klein four-group

In mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...

V. The inner automorphism group of Q is isomorphic to Q modulo its center, and is therefore also isomorphic to the Klein four-group. The full automorphism group of Q is isomorphic to S₄, the symmetric group

Symmetric group

In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...

on four letters. The outer automorphism group

Outer automorphism group

In mathematics, the outer automorphism group of a group Gis the quotient Aut / Inn, where Aut is the automorphism group of G and Inn is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted Out...

of Q is then S₄/V which is isomorphic to S₃.

Matrix representations

The quaternion group can be represented

Group representation

In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...

as a subgroup of the general linear group

General linear group

In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...

GL₂(C). A representation

is given by

Since all of the above matrices have unit determinant, this is a representation of Q in the special linear group

Special linear group

In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....

SL₂(C). The standard identities for quaternion multiplication can be verified using the usual laws of matrix multiplication in GL₂(C).
There is also an important action of Q on the eight nonzero elements of the 2-dimensional vector space over the finite field

Finite field

In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...

F₃. A representation

is given by

where {−1,0,1} are the three elements of F₃. Since all of the above matrices have unit determinant over F₃, this is a representation of Q in the special linear group SL(2, 3). Indeed, the group SL(2, 3) has order 24, and Q is a normal subgroup

Normal subgroup

In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....

of SL(2, 3) of index

Index of a subgroup

In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...

Galois group

As Richard Dean showed in 1981, the quaternion group can be presented as the Galois group

Galois group

In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...

Gal(T/Q) where Q is the field of rational number

Rational number

In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...

s and T is the splitting field

Splitting field

In abstract algebra, a splitting field of a polynomial with coefficients in a field is a smallest field extension of that field over which the polynomial factors into linear factors.-Definition:...

, over Q, of the polynomial

.
The development uses the fundamental theorem of Galois theory

Fundamental theorem of Galois theory

In mathematics, the fundamental theorem of Galois theory is a result that describes the structure of certain types of field extensions.In its most basic form, the theorem asserts that given a field extension E /F which is finite and Galois, there is a one-to-one correspondence between its...

in specifying four intermediate fields between Q and T and their Galois groups, as well as two theorems on cyclic extension of degree four over a field.

Generalized quaternion group

A group is called a generalized quaternion group or dicyclic group if it has a presentation

Presentation of a group

for some integer n ≥ 2. This group is denoted Q_4n and has order 4n. Coxeter labels these dicyclic groups <2,2,n>, being a special case of the binary polyhedral group and related to the polyhedral group

Polyhedral group

In geometry, the polyhedral group is any of the symmetry groups of the Platonic solids. There are three polyhedral groups:*The tetrahedral group of order 12, rotational symmetry group of the regular tetrahedron....

s (p,q,r), and dihedral group (2,2,n). The usual quaternion group corresponds to the case n = 2. The generalized quaternion group can be realized as the subgroup of GL₂(C) generated by

where ω_n = e^iπ/n. It can also be realized as the subgroup of unit quaternions generated by x = e^iπ/n and y = j.

The generalized quaternion groups have the property that every abelian

Abelian group

In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...

subgroup is cyclic. It can be shown that a finite p-group

P-group

In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...

with this property (every abelian subgroup is cyclic) is either cyclic or a generalized quaternion group as defined above. Another characterization is that a finite p-group in which there is a unique subgroup of order p is either cyclic or generalized quaternion (of order a power of 2). In particular, for a finite field F with odd characteristic, the 2-Sylow subgroup of SL₂(F) is non-abelian and has only one subgroup of order 2, so this 2-Sylow subgroup must be a generalized quaternion group, . Letting p^r be the size of F, where p is prime, the size of the 2-Sylow subgroup of SL₂(F) is 2ⁿ, where n = ord₂(p² - 1) + ord₂(r).

The Brauer-Suzuki theorem shows that groups whose Sylow 2-subgroup is generalized quaternion cannot be simple.