Yang–Mills
Encyclopedia
Yang–Mills theory is a gauge theory
based on the SU(N) group
. Wolfgang Pauli
formulated in 1953 the first consistent generalization of the five-dimensional theory of Kaluza, Klein
, Fock
and others to a higher dimensional internal space. Because Pauli saw no way to give masses to the gauge bosons, he refrained from publishing his results formally.
Although Pauli did not publish this theory, he gave talks widely attended by physicists of the time. In early 1954, Chen Ning Yang and Robert Mills
developed a modern formulation in an effort to extend the original concept of gauge theory
for abelian group
s, e.g. quantum electrodynamics
, to nonabelian group
s to provide an explanation for strong interactions. This initial idea was not a success, since the quanta
of the Yang–Mills field must be massless in order to maintain gauge invariance. The massless particles should have long range effects, but these effects are not seen in experiments. The idea was set aside until 1960, when the concept of particles acquiring mass through symmetry breaking
in massless theories was put forward, initially by Jeffrey Goldstone
, Yoichiro Nambu
, and Giovanni Jona-Lasinio
.
This prompted a significant restart of Yang–Mills theory studies that proved successful in the formulation of both electroweak unification
and quantum chromodynamics
(QCD). The electroweak interaction is described by SU(2)xU(1) group while QCD is an SU(3) gauge theory. The electroweak theory is obtained by combining SU(2) with U(1), where quantum electrodynamics (QED) is described by a U(1) group, and is replaced in the unified electroweak theory by a U(1) group representing a weak hypercharge rather than electric charge. The massless
bosons from the SU(2)xU(1) theory mix after spontaneous symmetry breaking to produce the 3 massive weak bosons, and the photon
field. The Standard Model
combines the strong interaction
, with the unified electroweak interaction (unifying the weak
and electromagnetic interaction) through the symmetry group SU(2)xU(1)xSU(3). In the current epoch the strong interaction is not unified with the electroweak interaction, but from the observed running of the coupling constants it is believed they all converge to a single value at very high energies.
Phenomenology at lower energies in quantum chromodynamics is not completely understood due to the difficulties of managing such a theory with a strong coupling. This is the reason confinement has not been theoretically proven, though it is a consistent experimental observation. Proof that QCD confines at low energy is a mathematical problem of great relevance, and an award has been proposed by the Clay Mathematics Institute
for whoever is also able to show that the Yang–Mills theory has a mass gap
and its existence.
with a non-abelian symmetry group given by the Lagrangian
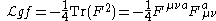
with the generators of the Lie algebra
corresponding to the F-quantities (the curvature
or field-strength form) satisfying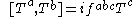
and the covariant derivative
defined as
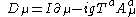
where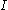
is the identity for the group generators, 
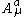is the vector potential, and 
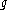is the coupling constant
. In four dimensions, the coupling constant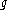
is a pure number and for a SU(N) group one has 
The relation
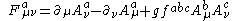
can be derived by the commutator
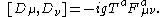
The field has the property of being self-interacting and equations of motion that one obtains are said to be semilinear, as nonlinearities are both with and without derivatives. This means that one can manage this theory only by perturbation theory
, with small nonlinearities.
Note that the transition between "upper" ("contravariant") and "lower" ("covariant") vector or tensor components is trivial for a indices (e.g.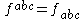
), whereas for μ and ν it is nontrivial, corresponding e.g. to the usual Lorentz signature, 
.
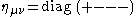From the given Lagrangian one can derive the equations of motion given by
Putting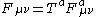
, these can be rewritten as
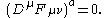
A Bianchi identity holds
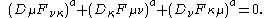
A source
enters into the equations of motion as
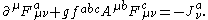
Note that the currents must properly change under gauge group transformations.
We give here some comments about the physical dimensions of the coupling. We note that, in D dimensions, the field scales as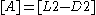
and so the coupling must scale as 
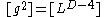. This implies that Yang–Mills theory is not renormalizable
for dimensions greater than four. Further, we note that, for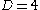
, the coupling is dimensionless and both the field and the square of the coupling have the same dimensions of the field and the coupling of a massless quartic scalar field theory
. So, these theories share the scale invariance
at the classical level.
. One introduces a generating functional for n-point functions as
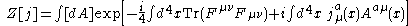
but this integral has no meaning as is because the potential vector can be arbitrarily chosen due to the gauge freedom. This problem was already known for quantum electrodynamics
but here becomes more severe due to non-abelian
properties of the gauge group. A way out has been given by Ludvig Faddeev
and Victor Popov
with the introduction of a ghost field (see Faddeev–Popov ghost) that has the property of being unphysical since, although it agrees with Fermi-Dirac statistics
, it is a complex scalar field, which violates the spin-statistics theorem
. So, we can write the generating functional as
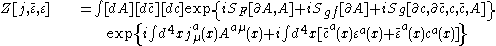
being
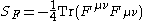
for the field,
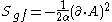
for the gauge fixing and
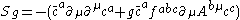
for the ghost. This is the expression commonly used to derive Feynman's rules (see Feynman diagram
). Here we have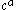
for the ghost field while 
fixes the gauge's choice for the quantization. Feynman's rules obtained from this functional are the following
These rules for Feynman diagrams can be obtained when we realize that the generating functional given above can be rewritten as
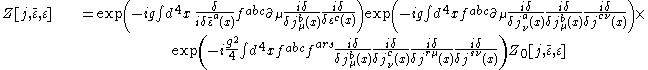
with
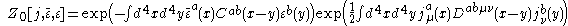
being the generating functional of the free theory. Expanding in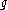
and computing the functional derivative
s, we are able to obtain all the n-point functions with perturbation theory. Using LSZ reduction formula
we get from the n-point functions the corresponding amplitudes for the given processes and cross section
s and decay rates are promptly obtained. The theory is renormalizable
and corrections are finite at any order of perturbation theory.
For quantum electrodynamics, where the gauge group is abelian, the ghost field decouples. This can be easily realized when we look at the coupling between the gauge field and the ghost field that is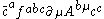
. For the abelian case, all the structure constants 
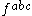are zero and so there is no coupling. In the non-abelian case, the ghost field appears as a useful way to rewrite the quantum field theory without physical consequences on the observables of the theory as cross sections or decay rates.
One of the most important results obtained for Yang–Mills theory is asymptotic freedom
. This result can be obtained assuming the coupling constant
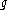is small (so small nonlinearities), as indeed happens to high energies, and applying perturbation theory
. The relevance of this result is due to the fact that a Yang–Mills theory that describes strong interaction and asymptotic freedom permits proper treatment of experimental results coming from deep inelastic scattering
.
In order to obtain the behavior of the Yang–Mills theory at high energies, and so to prove asymptotic freedom, one does perturbation theory assuming a small coupling. This is verified a posteriori
in the ultraviolet limit
. In the opposite limit, the infrared limit, the situation is quite the opposite, as the coupling is too large for perturbation theory to be reliable.
Indeed, most of the difficulties that current research meets is just managing the theory at low energies. That is the interesting case, being inherent to the description of hadronic matter and, more generally, to all the observed bound states of gluons and quarks and their confinement (see hadrons). The most used method to study the theory in this limit is to try to solve it on computers (see lattice gauge theory
). In this case, large computational resources are needed to be sure the right limit of infinite volume (smaller lattice spacing) is hit. This is the limit the results have to be compared with. Smaller spacing and larger coupling are not independent each other, and larger computational resources are demanded to accomplish both. As of today, the situation appears somewhat satisfactory for the hadronic spectrum and the computation of the gluon and ghost propagators, but the glueball
and hybrids
spectra are yet a questioned matter in view of the experimental observation of such exotic states. Indeed, the
resonance is not seen in any of such lattice computations and contrasting interpretations have been put forward. This is currently a hotly debated issue.
is the behavior over all the energy range of the running coupling. Such a behavior can be obtained from a theory once its beta function is known. Our ability to extract results from a quantum field theory relies on perturbation theory. Once the beta function is known, the behavior at all energy scales of the running coupling is obtained through the equation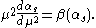
being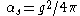
. Yang–Mills theory has the property of being asymptotically free
in the large energy limit (ultraviolet limit
). This means that, in this limit, the beta function has a minus sign driving the behavior of the running coupling toward even smaller values as the energy increases. Perturbation theory permits to evaluate beta function in this limit producing the following result for SU(N)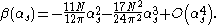
In the opposite limit of low energies (infrared limit), the beta function is not known. It is note the exact one for a supersymmetric
Yang–Mills theory. This has been obtained by Novikov, Shifman
, Vainshtein and Zakharov and can be written as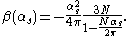
With this starting point, Thomas Ryttov and Francesco Sannino
were able to postulate a non-supersymmetric version of it writing down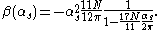
As can be seen from the beta function of the supersymmetric theory, the limit of a large coupling (infrared limit) implies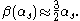
and so the running coupling in the deep infrared limit goes to zero making this theory trivial
. This implies that the coupling reaches a maximum at some value of the energy turning again to zero as the energy is lowered. Then, if Ryttov and Sannino hypothesis is correct, the same should be true for ordinary Yang–Mills theory. This would be in agreement with recent lattice computations.
. This applies even if the gauge bosons described by this theory are massive, as in the electroweak theory. However, the mass is only an "acquired" one, namely, as suggested, by the famous Higgs mechanism
.
Concerning the mathematics, it should be noted that presently, i.e. in 2011, the Yang–Mills theory is a very active field of research, yielding e.g. a classification of differentiable structures of four-dimensional manifolds by Simon Donaldson
. Furthermore, the field of Yang–Mills theories was included in the Clay Mathematics Institute
's list of "Millennium Prize Problems
". Here the prize-problem consists, especially, in a proof of the conjecture that the lowest excitations of a pure Yang–Mills theory (i.e. without matter fields) have a finite mass-gap with regard to the vacuum state. Another open problem, connected with this conjecture, is a proof of the confinement property in the presence of additional Fermion particles.
In physics the survey of Yang–Mills theories does not usually start from perturbation analysis or analytical methods, but more recently from systematic application of numerical methods to lattice gauge theories
.
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
based on the SU(N) group
Special unitary group
The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
. Wolfgang Pauli
Wolfgang Pauli
Wolfgang Ernst Pauli was an Austrian theoretical physicist and one of the pioneers of quantum physics. In 1945, after being nominated by Albert Einstein, he received the Nobel Prize in Physics for his "decisive contribution through his discovery of a new law of Nature, the exclusion principle or...
formulated in 1953 the first consistent generalization of the five-dimensional theory of Kaluza, Klein
Kaluza–Klein theory
In physics, Kaluza–Klein theory is a model that seeks to unify the two fundamental forces of gravitation and electromagnetism. The theory was first published in 1921. It was proposed by the mathematician Theodor Kaluza who extended general relativity to a five-dimensional spacetime...
, Fock
Vladimir Fock
Vladimir Aleksandrovich Fock was a Soviet physicist, who did foundational work on quantum mechanics and quantum electrodynamics....
and others to a higher dimensional internal space. Because Pauli saw no way to give masses to the gauge bosons, he refrained from publishing his results formally.
Although Pauli did not publish this theory, he gave talks widely attended by physicists of the time. In early 1954, Chen Ning Yang and Robert Mills
Robert Mills (physicist)
Robert L. Mills was a physicist, specializing in quantum field theory, the theory of alloys, and many-body theory. While sharing an office at Brookhaven National Laboratory, in 1954, Chen Ning Yang and Mills proposed a tensor equation for what are now called Yang-Mills fields...
developed a modern formulation in an effort to extend the original concept of gauge theory
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
for abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s, e.g. quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
, to nonabelian group
Nonabelian group
In mathematics, a non-abelian group, also sometimes called a non-commutative group, is a group in which there are at least two elements a and b of G such that a * b ≠ b * a...
s to provide an explanation for strong interactions. This initial idea was not a success, since the quanta
Quantum
In physics, a quantum is the minimum amount of any physical entity involved in an interaction. Behind this, one finds the fundamental notion that a physical property may be "quantized," referred to as "the hypothesis of quantization". This means that the magnitude can take on only certain discrete...
of the Yang–Mills field must be massless in order to maintain gauge invariance. The massless particles should have long range effects, but these effects are not seen in experiments. The idea was set aside until 1960, when the concept of particles acquiring mass through symmetry breaking
Symmetry breaking
Symmetry breaking in physics describes a phenomenon where small fluctuations acting on a system which is crossing a critical point decide the system's fate, by determining which branch of a bifurcation is taken. To an outside observer unaware of the fluctuations , the choice will appear arbitrary...
in massless theories was put forward, initially by Jeffrey Goldstone
Jeffrey Goldstone
Jeffrey Goldstone is a British-born theoretical physicist and an emeritus physics faculty at MIT Center for Theoretical Physics.He worked at the University of Cambridge until 1977....
, Yoichiro Nambu
Yoichiro Nambu
is a Japanese-born American physicist, currently a professor at the University of Chicago. Known for his contributions to the field of theoretical physics, he was awarded a one-half share of the Nobel Prize in Physics in 2008 for the discovery of the mechanism of spontaneous broken symmetry in...
, and Giovanni Jona-Lasinio
Giovanni Jona-Lasinio
Giovanni Jona-Lasinio , sometimes called Gianni Jona, is an influential Italian theoretical physicist, best known for his works on quantum field theory and statistical mechanics. He pioneered research concerning spontaneous symmetry breaking, and the Nambu–Jona-Lasinio model is named after him...
.
This prompted a significant restart of Yang–Mills theory studies that proved successful in the formulation of both electroweak unification
Electroweak interaction
In particle physics, the electroweak interaction is the unified description of two of the four known fundamental interactions of nature: electromagnetism and the weak interaction. Although these two forces appear very different at everyday low energies, the theory models them as two different...
and quantum chromodynamics
Quantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
(QCD). The electroweak interaction is described by SU(2)xU(1) group while QCD is an SU(3) gauge theory. The electroweak theory is obtained by combining SU(2) with U(1), where quantum electrodynamics (QED) is described by a U(1) group, and is replaced in the unified electroweak theory by a U(1) group representing a weak hypercharge rather than electric charge. The massless
bosons from the SU(2)xU(1) theory mix after spontaneous symmetry breaking to produce the 3 massive weak bosons, and the photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
field. The Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
combines the strong interaction
Strong interaction
In particle physics, the strong interaction is one of the four fundamental interactions of nature, the others being electromagnetism, the weak interaction and gravitation. As with the other fundamental interactions, it is a non-contact force...
, with the unified electroweak interaction (unifying the weak
Weak interaction
Weak interaction , is one of the four fundamental forces of nature, alongside the strong nuclear force, electromagnetism, and gravity. It is responsible for the radioactive decay of subatomic particles and initiates the process known as hydrogen fusion in stars...
and electromagnetic interaction) through the symmetry group SU(2)xU(1)xSU(3). In the current epoch the strong interaction is not unified with the electroweak interaction, but from the observed running of the coupling constants it is believed they all converge to a single value at very high energies.
Phenomenology at lower energies in quantum chromodynamics is not completely understood due to the difficulties of managing such a theory with a strong coupling. This is the reason confinement has not been theoretically proven, though it is a consistent experimental observation. Proof that QCD confines at low energy is a mathematical problem of great relevance, and an award has been proposed by the Clay Mathematics Institute
Clay Mathematics Institute
The Clay Mathematics Institute is a private, non-profit foundation, based in Cambridge, Massachusetts. The Institute is dedicated to increasing and disseminating mathematical knowledge. It gives out various awards and sponsorships to promising mathematicians. The institute was founded in 1998...
for whoever is also able to show that the Yang–Mills theory has a mass gap
Mass gap
In quantum field theory, the mass gap is the difference in energy between the vacuum and the next lowest energy state. The energy of the vacuum is zero by definition, and assuming that all energy states can be thought of as particles in plane-waves, the mass gap is the mass of the lightest...
and its existence.
Mathematical overview
Yang–Mills theories are a special example of gauge theoryGauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
with a non-abelian symmetry group given by the Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
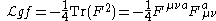
with the generators of the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
corresponding to the F-quantities (the curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
or field-strength form) satisfying
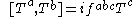
and the covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
defined as
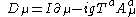
where
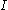is the identity for the group generators, 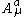is the vector potential, and 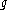is the coupling constantCoupling constant
In physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
. In four dimensions, the coupling constant
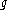is a pure number and for a SU(N) group one has The relation
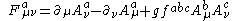
can be derived by the commutator
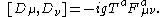
The field has the property of being self-interacting and equations of motion that one obtains are said to be semilinear, as nonlinearities are both with and without derivatives. This means that one can manage this theory only by perturbation theory
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
, with small nonlinearities.
Note that the transition between "upper" ("contravariant") and "lower" ("covariant") vector or tensor components is trivial for a indices (e.g.
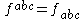), whereas for μ and ν it is nontrivial, corresponding e.g. to the usual Lorentz signature, 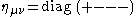.From the given Lagrangian one can derive the equations of motion given by
Putting
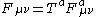, these can be rewritten as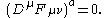A Bianchi identity holds
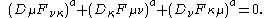
A source
enters into the equations of motion as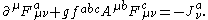Note that the currents must properly change under gauge group transformations.
We give here some comments about the physical dimensions of the coupling. We note that, in D dimensions, the field scales as
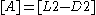and so the coupling must scale as 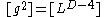. This implies that Yang–Mills theory is not renormalizableRenormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
for dimensions greater than four. Further, we note that, for
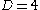, the coupling is dimensionless and both the field and the square of the coupling have the same dimensions of the field and the coupling of a massless quartic scalar field theoryScalar field theory
In theoretical physics, scalar field theory can refer to a classical or quantum theory of scalar fields. A field which is invariant under any Lorentz transformation is called a "scalar", in contrast to a vector or tensor field...
. So, these theories share the scale invariance
Scale invariance
In physics and mathematics, scale invariance is a feature of objects or laws that do not change if scales of length, energy, or other variables, are multiplied by a common factor...
at the classical level.
Quantization of Yang–Mills theory
The most appropriate method to quantize the Yang–Mills theory is by functional methods, i.e. path integralsPath integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
. One introduces a generating functional for n-point functions as
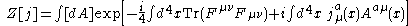
but this integral has no meaning as is because the potential vector can be arbitrarily chosen due to the gauge freedom. This problem was already known for quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
but here becomes more severe due to non-abelian
Non-abelian
In theoretical physics, a non-abelian gauge transformation means a gauge transformation taking values in some group G, the elements of which do not obey the commutative law when they are multiplied. The original choice of G in the physics of electromagnetism was U, which is commutative.For a...
properties of the gauge group. A way out has been given by Ludvig Faddeev
Ludvig Faddeev
-References:...
and Victor Popov
Victor Popov
Victor Nikolaevich Popov was a Russian theoretical physicist known for his contribution to the quantization of non-abelian gauge fields. His work with Ludvig Faddeev on that subject introduced the fundamental objects now known as Faddeev–Popov ghosts....
with the introduction of a ghost field (see Faddeev–Popov ghost) that has the property of being unphysical since, although it agrees with Fermi-Dirac statistics
Fermi-Dirac statistics
Fermi–Dirac statistics is a part of the science of physics that describes the energies of single particles in a system comprising many identical particles that obey the Pauli Exclusion Principle...
, it is a complex scalar field, which violates the spin-statistics theorem
Spin-statistics theorem
In quantum mechanics, the spin-statistics theorem relates the spin of a particle to the particle statistics it obeys. The spin of a particle is its intrinsic angular momentum...
. So, we can write the generating functional as
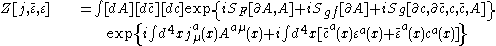
being
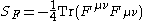
for the field,
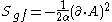
for the gauge fixing and
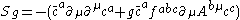
for the ghost. This is the expression commonly used to derive Feynman's rules (see Feynman diagram
Feynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
). Here we have
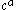for the ghost field while fixes the gauge's choice for the quantization. Feynman's rules obtained from this functional are the followingThese rules for Feynman diagrams can be obtained when we realize that the generating functional given above can be rewritten as
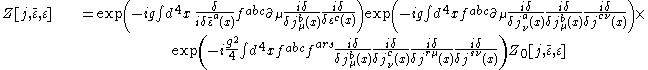
with
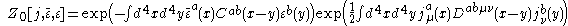
being the generating functional of the free theory. Expanding in
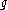and computing the functional derivativeFunctional derivative
In mathematics and theoretical physics, the functional derivative is a generalization of the gradient. While the latter differentiates with respect to a vector with discrete components, the former differentiates with respect to a continuous function. Both of these can be viewed as extensions of...
s, we are able to obtain all the n-point functions with perturbation theory. Using LSZ reduction formula
LSZ reduction formula
In quantum field theory, the LSZ reduction formula is a method to calculate p-matrix elements from the time-ordered correlation functions of a quantum field theory. It is a step of the path that starts from the Lagrangian of some quantum field theory and leads to prediction of measurable quantities...
we get from the n-point functions the corresponding amplitudes for the given processes and cross section
Cross section (physics)
A cross section is the effective area which governs the probability of some scattering or absorption event. Together with particle density and path length, it can be used to predict the total scattering probability via the Beer-Lambert law....
s and decay rates are promptly obtained. The theory is renormalizable
Renormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
and corrections are finite at any order of perturbation theory.
For quantum electrodynamics, where the gauge group is abelian, the ghost field decouples. This can be easily realized when we look at the coupling between the gauge field and the ghost field that is
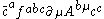. For the abelian case, all the structure constants 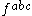are zero and so there is no coupling. In the non-abelian case, the ghost field appears as a useful way to rewrite the quantum field theory without physical consequences on the observables of the theory as cross sections or decay rates.One of the most important results obtained for Yang–Mills theory is asymptotic freedom
Asymptotic freedom
In physics, asymptotic freedom is a property of some gauge theories that causes interactions between particles to become arbitrarily weak at energy scales that become arbitrarily large, or, equivalently, at length scales that become arbitrarily small .Asymptotic freedom is a feature of quantum...
. This result can be obtained assuming the coupling constant
Coupling constant
In physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
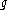is small (so small nonlinearities), as indeed happens to high energies, and applying perturbation theoryPerturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
. The relevance of this result is due to the fact that a Yang–Mills theory that describes strong interaction and asymptotic freedom permits proper treatment of experimental results coming from deep inelastic scattering
Deep Inelastic Scattering
Deep inelastic scattering is the name given to a process used to probe the insides of hadrons , using electrons, muons and neutrinos. It provided the first convincing evidence of the reality of quarks, which up until that point had been considered by many to be a purely mathematical phenomenon...
.
In order to obtain the behavior of the Yang–Mills theory at high energies, and so to prove asymptotic freedom, one does perturbation theory assuming a small coupling. This is verified a posteriori
A Posteriori
Apart from the album, some additional remixes were released exclusively through the iTunes Store. They are:*"Eppur si muove" – 6:39*"Dreaming of Andromeda" Apart from the album, some additional remixes were released exclusively through the iTunes Store. They are:*"Eppur si muove" (Tocadisco...
in the ultraviolet limit
Ultraviolet divergence
In physics, an ultraviolet divergence is a situation in which an integral, for example a Feynman diagram, diverges because of contributions of objects with very high energy , or, equivalently, because of physical phenomena at very short distances. An infinite answer to a question that should have a...
. In the opposite limit, the infrared limit, the situation is quite the opposite, as the coupling is too large for perturbation theory to be reliable.
Indeed, most of the difficulties that current research meets is just managing the theory at low energies. That is the interesting case, being inherent to the description of hadronic matter and, more generally, to all the observed bound states of gluons and quarks and their confinement (see hadrons). The most used method to study the theory in this limit is to try to solve it on computers (see lattice gauge theory
Lattice gauge theory
In physics, lattice gauge theory is the study of gauge theories on a spacetime that has been discretized into a lattice. Gauge theories are important in particle physics, and include the prevailing theories of elementary particles: quantum electrodynamics, quantum chromodynamics and the Standard...
). In this case, large computational resources are needed to be sure the right limit of infinite volume (smaller lattice spacing) is hit. This is the limit the results have to be compared with. Smaller spacing and larger coupling are not independent each other, and larger computational resources are demanded to accomplish both. As of today, the situation appears somewhat satisfactory for the hadronic spectrum and the computation of the gluon and ghost propagators, but the glueball
Glueball
In particle physics, a glueball is a hypothetical composite particle. It consists solely of gluon particles, without valence quarks. Such a state is possible because gluons carry color charge and experience the strong interaction...
and hybrids
Exotic meson
Non-quark model mesons include#exotic mesons, which have quantum numbers not possible for mesons in the quark model;#glueballs or gluonium, which have no valence quarks at all;...
spectra are yet a questioned matter in view of the experimental observation of such exotic states. Indeed, the
resonance is not seen in any of such lattice computations and contrasting interpretations have been put forward. This is currently a hotly debated issue.Beta function
One of the key properties of a quantum field theoryQuantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
is the behavior over all the energy range of the running coupling. Such a behavior can be obtained from a theory once its beta function is known. Our ability to extract results from a quantum field theory relies on perturbation theory. Once the beta function is known, the behavior at all energy scales of the running coupling is obtained through the equation
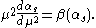
being
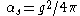. Yang–Mills theory has the property of being asymptotically freeAsymptotic freedom
In physics, asymptotic freedom is a property of some gauge theories that causes interactions between particles to become arbitrarily weak at energy scales that become arbitrarily large, or, equivalently, at length scales that become arbitrarily small .Asymptotic freedom is a feature of quantum...
in the large energy limit (ultraviolet limit
Ultraviolet divergence
In physics, an ultraviolet divergence is a situation in which an integral, for example a Feynman diagram, diverges because of contributions of objects with very high energy , or, equivalently, because of physical phenomena at very short distances. An infinite answer to a question that should have a...
). This means that, in this limit, the beta function has a minus sign driving the behavior of the running coupling toward even smaller values as the energy increases. Perturbation theory permits to evaluate beta function in this limit producing the following result for SU(N)
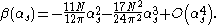
In the opposite limit of low energies (infrared limit), the beta function is not known. It is note the exact one for a supersymmetric
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
Yang–Mills theory. This has been obtained by Novikov, Shifman
Mikhail Shifman
-External links:*****...
, Vainshtein and Zakharov and can be written as
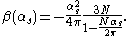
With this starting point, Thomas Ryttov and Francesco Sannino
Francesco Sannino
Francesco Sannino is an Italian theoretical physicist and a professor at the University of Southern Denmark. He is an expert in effective field theories and their applications to strongly coupled theories such as quantum chromodynamics. He is also an expert in beyond standard model physics and...
were able to postulate a non-supersymmetric version of it writing down
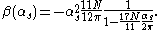
As can be seen from the beta function of the supersymmetric theory, the limit of a large coupling (infrared limit) implies
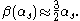
and so the running coupling in the deep infrared limit goes to zero making this theory trivial
Quantum triviality
In a quantum field theory, charge screening can restrict the value of the observable "renormalized" charge of a classical theory. Ifthe only allowed value of the renormalized charge is zero, the theory is said to be "trivial" or noninteracting...
. This implies that the coupling reaches a maximum at some value of the energy turning again to zero as the energy is lowered. Then, if Ryttov and Sannino hypothesis is correct, the same should be true for ordinary Yang–Mills theory. This would be in agreement with recent lattice computations.
Open problems
The Yang–Mills theories were generally acknowledged in the physics community after Gerard 't Hooft, in 1972, could prove their renormalizabilityRenormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
. This applies even if the gauge bosons described by this theory are massive, as in the electroweak theory. However, the mass is only an "acquired" one, namely, as suggested, by the famous Higgs mechanism
Higgs mechanism
In particle physics, the Higgs mechanism is the process in which gauge bosons in a gauge theory can acquire non-vanishing masses through absorption of Nambu-Goldstone bosons arising in spontaneous symmetry breaking....
.
Concerning the mathematics, it should be noted that presently, i.e. in 2011, the Yang–Mills theory is a very active field of research, yielding e.g. a classification of differentiable structures of four-dimensional manifolds by Simon Donaldson
Simon Donaldson
Simon Kirwan Donaldson FRS , is an English mathematician known for his work on the topology of smooth four-dimensional manifolds. He is now Royal Society research professor in Pure Mathematics and President of the Institute for Mathematical Science at Imperial College London...
. Furthermore, the field of Yang–Mills theories was included in the Clay Mathematics Institute
Clay Mathematics Institute
The Clay Mathematics Institute is a private, non-profit foundation, based in Cambridge, Massachusetts. The Institute is dedicated to increasing and disseminating mathematical knowledge. It gives out various awards and sponsorships to promising mathematicians. The institute was founded in 1998...
's list of "Millennium Prize Problems
Millennium Prize Problems
The Millennium Prize Problems are seven problems in mathematics that were stated by the Clay Mathematics Institute in 2000. As of September 2011, six of the problems remain unsolved. A correct solution to any of the problems results in a US$1,000,000 prize being awarded by the institute...
". Here the prize-problem consists, especially, in a proof of the conjecture that the lowest excitations of a pure Yang–Mills theory (i.e. without matter fields) have a finite mass-gap with regard to the vacuum state. Another open problem, connected with this conjecture, is a proof of the confinement property in the presence of additional Fermion particles.
In physics the survey of Yang–Mills theories does not usually start from perturbation analysis or analytical methods, but more recently from systematic application of numerical methods to lattice gauge theories
Lattice gauge theory
In physics, lattice gauge theory is the study of gauge theories on a spacetime that has been discretized into a lattice. Gauge theories are important in particle physics, and include the prevailing theories of elementary particles: quantum electrodynamics, quantum chromodynamics and the Standard...
.
See also
- Yang–Mills existence and mass gapYang–Mills existence and mass gapIn mathematics, the Yang-Mills existence and mass gap problem is an unsolved problem and one of the seven Millennium Prize Problems defined by the Clay Mathematics Institute which has offered a prize of US$1,000,000 to a person solving it....
- Aharonov-Bohm effectAharonov-Bohm effectThe Aharonov–Bohm effect, sometimes called the Ehrenberg–Siday–Aharonov–Bohm effect, is a quantum mechanical phenomenon in which an electrically charged particle is affected by an electromagnetic field , despite being confined to a region in which both the magnetic field B and electric field E are...
- Coulomb gauge
- Electroweak theory
- Field theoretical formulation of the standard modelStandard model (basic details)This is a detailed description of the standard model of particle physics. It describes how the leptons, quarks, gauge bosons and the Higgs particle fit together...
- Gauge covariant derivativeGauge covariant derivativeThe gauge covariant derivative is like a generalization of the covariant derivative used in general relativity. If a theory has gauge transformations, it means that some physical properties of certain equations are preserved under those transformations...
- Kaluza-Klein theory
- Lorenz gauge
- Quantum chromodynamicsQuantum chromodynamicsIn theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
- Quantum gauge theoryQuantum gauge theoryIn quantum physics, in order to quantize a gauge theory, like for example Yang-Mills theory, Chern-Simons or BF model, one method is to perform a gauge fixing. This is done in the BRST and Batalin-Vilkovisky formulation...
- Symmetry in physicsSymmetry in physicsIn physics, symmetry includes all features of a physical system that exhibit the property of symmetry—that is, under certain transformations, aspects of these systems are "unchanged", according to a particular observation...
- Weyl gauge
- Yang–Mills–Higgs equationsYang–Mills–Higgs equationsIn mathematics, the Yang–Mills–Higgs equations are a set of non-linear partial differential equations for a Yang–Mills field, given by a connection, and a Higgs field, given by a section of a vector bundle...