
Binary icosahedral group
Encyclopedia
In mathematics
, the binary icosahedral group 2I or <2,3,5> is a certain nonabelian group
of order
120.
It is an extension
of the icosahedral group I or (2,3,5) of order 60 by a cyclic group
of order 2, and is the preimage of the icosahedral group under the 2:1 covering homomorphism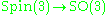
of the special orthogonal group by the spin group. It follows that the binary icosahedral group is discrete subgroup of Spin(3) of order 120.
It should not be confused with the full icosahedral group, which is a different group of order 120, and is rather a subgroup of the orthogonal group
O(3).
The binary icosahedral group is most easily described concretely as a discrete subgroup of the unit quaternion
s, under the isomorphism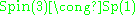 where Sp(1) is the multiplicative group of unit quaternions. (For a description of this homomorphism see the article on quaternions and spatial rotation
where Sp(1) is the multiplicative group of unit quaternions. (For a description of this homomorphism see the article on quaternions and spatial rotation
s.)
with all 96 quaternions obtained from
by an even permutation of coordinates (all possible sign combinations). Here φ = ½ (1 + √5) is the golden ratio
.
In total there are 120 elements, namely the unit icosian
s. They all have unit magnitude and therefore lie in the unit quaternion group Sp(1). The convex hull
of these 120 elements in 4-dimensional space form a regular polychoron, known as the 600-cell.
Explicitly, it fits into the short exact sequence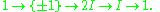
This sequence does not split, meaning that 2I is not a semidirect product
of { ±1 } by I. In fact, there is no subgroup of 2I isomorphic to I.
The center of 2I is the subgroup { ±1 }, so that the inner automorphism group is isomorphic to I. The full automorphism group is isomorphic to S5 (the symmetric group
on 5 letters), just as for - any automorphism of 2I fixes the non-trivial element of the center (
- any automorphism of 2I fixes the non-trivial element of the center (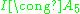 ), hence descends to an automorphism of I, and conversely, any automorphism of I lifts to an automorphism of 2I, since the lift of generators of I are generators of 2I (different lifts give the same automorphism).
), hence descends to an automorphism of I, and conversely, any automorphism of I lifts to an automorphism of 2I, since the lift of generators of I are generators of 2I (different lifts give the same automorphism).
, meaning that it is equal to its commutator subgroup
. In fact, 2I is the unique perfect group of order 120. It follows that 2I is not solvable
.
Further, the binary icosahedral group is superperfect, meaning abstractly that its first two group homology groups vanish: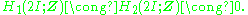 Concretely, this means that its abelianization is trivial (it has no non-trivial abelian quotients) and that its Schur multiplier
Concretely, this means that its abelianization is trivial (it has no non-trivial abelian quotients) and that its Schur multiplier
is trivial (it has no non-trivial perfect central extensions). In fact, the binary icosahedral group is the smallest (non-trivial) superperfect group.
The binary icosahedral group is not acyclic, however, as Hn(2I,Z) is cyclic of order 120 for n = 4k+3, and trivial for n > 0 otherwise, .
, which is a subgroup of SO(4), and the binary icosahedral group is isomorphic to the double cover of this in Spin(4). Note that the symmetric group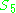 does have a 4-dimensional representation (its usual lowest-dimensional irreducible representation as the full symmetries of the
does have a 4-dimensional representation (its usual lowest-dimensional irreducible representation as the full symmetries of the  -simplex), and that the full symmetries of the 4-simplex are thus
-simplex), and that the full symmetries of the 4-simplex are thus  not the full icosahedral group (these are two different groups of order 120).
not the full icosahedral group (these are two different groups of order 120).
The binary icosahedral group can be considered as the double cover of the alternating group
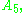 denoted
denoted  this isomorphism covers the isomorphism of the icosahedral group with the alternating group
this isomorphism covers the isomorphism of the icosahedral group with the alternating group  and can be thought of as sitting as subgroups of Spin(4) and SO(4) (and inside the symmetric group
and can be thought of as sitting as subgroups of Spin(4) and SO(4) (and inside the symmetric group 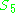 and either of its double covers
and either of its double covers 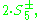 in turn sitting inside either pin group and the orthogonal group
in turn sitting inside either pin group and the orthogonal group 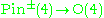 ).
).
Unlike the icosahedral group, which is exceptional
to 3 dimensions, these tetrahedral groups and alternating groups (and their double covers) exist in all higher dimensions.
One can show that the binary icosahedral group is isomorphic to the special linear group
SL(2,5) — the group of all 2×2 matrices over the finite field
F5 with unit determinant; this covers the exceptional isomorphism of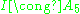 with the projective special linear group PSL(2,5).
with the projective special linear group PSL(2,5).
Note also the exceptional isomorphism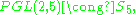 which is a different group of order 120, with the commutative square of SL, GL, PSL, PGL being isomorphic to a commutative square of
which is a different group of order 120, with the commutative square of SL, GL, PSL, PGL being isomorphic to a commutative square of 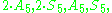 which are isomorphic to subgroups of the commutative square of Spin(4), Pin(4), SO(4), O(4).
which are isomorphic to subgroups of the commutative square of Spin(4), Pin(4), SO(4), O(4).
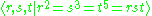
or equivalently,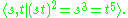
Generators with these relations are given by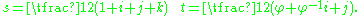
of 2I is the center { ±1 }.
By the third isomorphism theorem, there is a Galois connection
between subgroups of 2I and subgroups of I, where the closure operator
on subgroups of 2I is multiplication by { ±1 }.
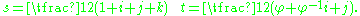 is the only element of order 2, hence it is contained in all subgroups of even order: thus every subgroup of 2I is either of odd order or is the preimage of a subgroup of I.
is the only element of order 2, hence it is contained in all subgroups of even order: thus every subgroup of 2I is either of odd order or is the preimage of a subgroup of I.
Besides the cyclic group
s generated by the various elements (which can have odd order), the only other subgroups of 2I (up to conjugation) are:
Ih is the symmetry group of the 600-cell (also that of its dual, the 120-cell). Just as the former is the Coxeter group
of type H3, the latter is the Coxeter group of type H4, also denoted [3,3,5]. Its rotational subgroup, denoted [3,3,5]+ is a group of order 7200 living in SO(4)
. SO(4) has a double cover called Spin(4) in much the same way that Spin(3) is the double cover of SO(3). Similar to the isomorphism Spin(3) = Sp(1), the group Spin(4) is isomorphic to Sp(1) × Sp(1).
The preimage of [3,3,5]+ in Spin(4) (a four-dimensional analogue of 2I) is precisely the product group
2I × 2I of order 14400. The rotational symmetry group of the 600-cell is then
Various other 4-dimensional symmetry groups can be constructed from 2I. For details, see (Conway and Smith, 2003).
called the Poincaré homology sphere. It is an example of a homology sphere
, i.e. a 3-manifold whose homology groups are identical to those of a 3-sphere
. The fundamental group
of the Poincaré sphere is isomorphic to the binary icosahedral group, as the Poincaré sphere is the quotient of a 3-sphere by the binary icosahedral group.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the binary icosahedral group 2I or <2,3,5> is a certain nonabelian group
Nonabelian group
In mathematics, a non-abelian group, also sometimes called a non-commutative group, is a group in which there are at least two elements a and b of G such that a * b ≠ b * a...
of order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
120.
It is an extension
Group extension
In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence...
of the icosahedral group I or (2,3,5) of order 60 by a cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order 2, and is the preimage of the icosahedral group under the 2:1 covering homomorphism
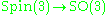
of the special orthogonal group by the spin group. It follows that the binary icosahedral group is discrete subgroup of Spin(3) of order 120.
It should not be confused with the full icosahedral group, which is a different group of order 120, and is rather a subgroup of the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
O(3).
The binary icosahedral group is most easily described concretely as a discrete subgroup of the unit quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s, under the isomorphism
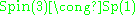 where Sp(1) is the multiplicative group of unit quaternions. (For a description of this homomorphism see the article on quaternions and spatial rotation
where Sp(1) is the multiplicative group of unit quaternions. (For a description of this homomorphism see the article on quaternions and spatial rotationQuaternions and spatial rotation
Unit quaternions provide a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. Compared to Euler angles they are simpler to compose and avoid the problem of gimbal lock. Compared to rotation matrices they are more numerically stable and may...
s.)
Elements
Explicitly, the binary icosahedral group is given as the union of the 24 Hurwitz units- { ±1, ±i, ±j, ±k, ½ ( ±1 ± i ± j ± k ) }
with all 96 quaternions obtained from
- ½ ( 0 ± i ± φ−1j ± φk )
by an even permutation of coordinates (all possible sign combinations). Here φ = ½ (1 + √5) is the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
.
In total there are 120 elements, namely the unit icosian
Icosian
In mathematics, the icosians are a specific set of Hamiltonian quaternions with the same symmetry as the 600-cell. The term can be used to refer to two related, but distinct, concepts:...
s. They all have unit magnitude and therefore lie in the unit quaternion group Sp(1). The convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of these 120 elements in 4-dimensional space form a regular polychoron, known as the 600-cell.
Central extension
The binary icosahedral group, denoted by 2I, is the universal perfect central extension of the icosahedral group, and thus is quasisimple: it is a perfect central extension of a simple group.Explicitly, it fits into the short exact sequence
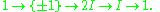
This sequence does not split, meaning that 2I is not a semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of { ±1 } by I. In fact, there is no subgroup of 2I isomorphic to I.
The center of 2I is the subgroup { ±1 }, so that the inner automorphism group is isomorphic to I. The full automorphism group is isomorphic to S5 (the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on 5 letters), just as for
 - any automorphism of 2I fixes the non-trivial element of the center (
- any automorphism of 2I fixes the non-trivial element of the center (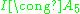 ), hence descends to an automorphism of I, and conversely, any automorphism of I lifts to an automorphism of 2I, since the lift of generators of I are generators of 2I (different lifts give the same automorphism).
), hence descends to an automorphism of I, and conversely, any automorphism of I lifts to an automorphism of 2I, since the lift of generators of I are generators of 2I (different lifts give the same automorphism).Superperfect
The binary icosahedral group is perfectPerfect group
In mathematics, more specifically in the area of modern algebra known as group theory, a group is said to be perfect if it equals its own commutator subgroup, or equivalently, if the group has no nontrivial abelian quotients...
, meaning that it is equal to its commutator subgroup
Commutator subgroup
In mathematics, more specifically in abstract algebra, the commutator subgroup or derived subgroup of a group is the subgroup generated by all the commutators of the group....
. In fact, 2I is the unique perfect group of order 120. It follows that 2I is not solvable
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
.
Further, the binary icosahedral group is superperfect, meaning abstractly that its first two group homology groups vanish:
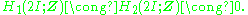 Concretely, this means that its abelianization is trivial (it has no non-trivial abelian quotients) and that its Schur multiplier
Concretely, this means that its abelianization is trivial (it has no non-trivial abelian quotients) and that its Schur multiplierSchur multiplier
In mathematical group theory, the Schur multiplier or Schur multiplicator is the second homology group H_2 of a group G.It was introduced by in his work on projective representations.-Examples and properties:...
is trivial (it has no non-trivial perfect central extensions). In fact, the binary icosahedral group is the smallest (non-trivial) superperfect group.
The binary icosahedral group is not acyclic, however, as Hn(2I,Z) is cyclic of order 120 for n = 4k+3, and trivial for n > 0 otherwise, .
Isomorphisms
Concretely, the binary icosahedral group is a subgroup of Spin(3), and covers the icosahedral group, which is a subgroup of SO(3). Abstractly, the icosahedral group is isomorphic to the symmetries of the 4-simplexSimplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
, which is a subgroup of SO(4), and the binary icosahedral group is isomorphic to the double cover of this in Spin(4). Note that the symmetric group
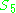 does have a 4-dimensional representation (its usual lowest-dimensional irreducible representation as the full symmetries of the
does have a 4-dimensional representation (its usual lowest-dimensional irreducible representation as the full symmetries of the 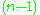 -simplex), and that the full symmetries of the 4-simplex are thus
-simplex), and that the full symmetries of the 4-simplex are thus 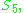 not the full icosahedral group (these are two different groups of order 120).
not the full icosahedral group (these are two different groups of order 120).The binary icosahedral group can be considered as the double cover of the alternating group
Covering groups of the alternating and symmetric groups
In the mathematical area of group theory, the covering groups of the alternating and symmetric groups are groups that are used to understand the projective representations of the alternating and symmetric groups...
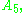 denoted
denoted  this isomorphism covers the isomorphism of the icosahedral group with the alternating group
this isomorphism covers the isomorphism of the icosahedral group with the alternating group  and can be thought of as sitting as subgroups of Spin(4) and SO(4) (and inside the symmetric group
and can be thought of as sitting as subgroups of Spin(4) and SO(4) (and inside the symmetric group 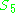 and either of its double covers
and either of its double covers 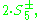 in turn sitting inside either pin group and the orthogonal group
in turn sitting inside either pin group and the orthogonal group 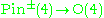 ).
).Unlike the icosahedral group, which is exceptional
Exceptional object
Many branches of mathematics study objects of a given type and prove a classification theorem. A common theme is that the classification results in a number of series of objects as well as a finite number of exceptions that don't fit into any series. These are known as exceptional...
to 3 dimensions, these tetrahedral groups and alternating groups (and their double covers) exist in all higher dimensions.
One can show that the binary icosahedral group is isomorphic to the special linear group
Special linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
SL(2,5) — the group of all 2×2 matrices over the finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
F5 with unit determinant; this covers the exceptional isomorphism of
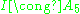 with the projective special linear group PSL(2,5).
with the projective special linear group PSL(2,5).Note also the exceptional isomorphism
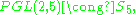 which is a different group of order 120, with the commutative square of SL, GL, PSL, PGL being isomorphic to a commutative square of
which is a different group of order 120, with the commutative square of SL, GL, PSL, PGL being isomorphic to a commutative square of 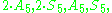 which are isomorphic to subgroups of the commutative square of Spin(4), Pin(4), SO(4), O(4).
which are isomorphic to subgroups of the commutative square of Spin(4), Pin(4), SO(4), O(4).Presentation
The group 2I has a presentation given by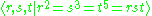
or equivalently,
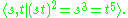
Generators with these relations are given by
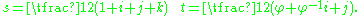
Subgroups
The only proper normal subgroupNormal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of 2I is the center { ±1 }.
By the third isomorphism theorem, there is a Galois connection
Galois connection
In mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...
between subgroups of 2I and subgroups of I, where the closure operator
Closure operator
In mathematics, a closure operator on a set S is a function cl: P → P from the power set of S to itself which satisfies the following conditions for all sets X,Y ⊆ S....
on subgroups of 2I is multiplication by { ±1 }.
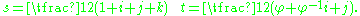 is the only element of order 2, hence it is contained in all subgroups of even order: thus every subgroup of 2I is either of odd order or is the preimage of a subgroup of I.
is the only element of order 2, hence it is contained in all subgroups of even order: thus every subgroup of 2I is either of odd order or is the preimage of a subgroup of I.Besides the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
s generated by the various elements (which can have odd order), the only other subgroups of 2I (up to conjugation) are:
- binary dihedral groups of orders 12 and 20 (covering the dihedral groups D3 and D5 in I).
- The quaternion groupQuaternion groupIn group theory, the quaternion group is a non-abelian group of order eight, isomorphic to a certain eight-element subset of the quaternions under multiplication...
consisting of the 8 Lipschitz units forms a subgroup of index 15, which is also the dicyclic group Dic2; this covers the stabilizer of an edge. - The 24 Hurwitz units form an index 5 subgroup called the binary tetrahedral group; this covers a chiral tetrahedral group. This group is self-normalizing so its conjugacy classConjugacy classIn mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
has 5 members (this gives a map whose image is
whose image is  ).
).
Relation to 4-dimensional symmetry groups
The 4-dimensional analog of the icosahedral symmetry groupIcosahedral symmetry
A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...
Ih is the symmetry group of the 600-cell (also that of its dual, the 120-cell). Just as the former is the Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
of type H3, the latter is the Coxeter group of type H4, also denoted [3,3,5]. Its rotational subgroup, denoted [3,3,5]+ is a group of order 7200 living in SO(4)
SO(4)
In mathematics, the group of rotations about a fixed point in four-dimensional Euclidean space is denoted SO. The name comes from the fact that it is the special orthogonal group of order 4....
. SO(4) has a double cover called Spin(4) in much the same way that Spin(3) is the double cover of SO(3). Similar to the isomorphism Spin(3) = Sp(1), the group Spin(4) is isomorphic to Sp(1) × Sp(1).
The preimage of [3,3,5]+ in Spin(4) (a four-dimensional analogue of 2I) is precisely the product group
Direct product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
2I × 2I of order 14400. The rotational symmetry group of the 600-cell is then
- [3,3,5]+ = ( 2I × 2I ) / { ±1 }.
Various other 4-dimensional symmetry groups can be constructed from 2I. For details, see (Conway and Smith, 2003).
Applications
The coset space Spin(3) / 2I = S3 / 2I is a spherical 3-manifoldSpherical 3-manifold
In mathematics, a spherical 3-manifold M is a 3-manifold of the formM=S^3/\Gammawhere \Gamma is a finite subgroup of SO acting freely by rotations on the 3-sphere S^3. All such manifolds are prime, orientable, and closed...
called the Poincaré homology sphere. It is an example of a homology sphere
Homology sphere
In algebraic topology, a homology sphere is an n-manifold X having the homology groups of an n-sphere, for some integer n ≥ 1. That is,andTherefore X is a connected space, with one non-zero higher Betti number: bn...
, i.e. a 3-manifold whose homology groups are identical to those of a 3-sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
. The fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of the Poincaré sphere is isomorphic to the binary icosahedral group, as the Poincaré sphere is the quotient of a 3-sphere by the binary icosahedral group.
See also
- binary polyhedral group
- binary cyclic group
- binary dihedral group
- binary tetrahedral group
- binary octahedral group

