Ideal (ring theory)
Encyclopedia
In ring theory
, a branch of abstract algebra
, an ideal is a special subset
of a ring
. The ideal concept allows the generalization in an appropriate way of some important properties of integer
s like "even number" or "multiple of 3".
For instance, in rings one studies prime ideal
s instead of prime number
s, one defines coprime ideals as a generalization of coprime numbers
, and one can prove a generalized Chinese remainder theorem
about ideals. In a certain class of rings important in number theory
, the Dedekind domain
s, one can even recover a version of the fundamental theorem of arithmetic
: in these rings, every nonzero ideal can be uniquely written as a product of prime ideals.
An ideal can be used to construct a quotient ring
in a similar way as a normal subgroup
in group theory
can be used to construct a quotient group
. The concept of an order ideal in order theory
is derived from the notion of ideal in ring theory.
A fractional ideal
is a generalization of an ideal, and the usual ideals are sometimes called integral ideals for clarity.
in 1876 in the third edition of his book Vorlesungen über Zahlentheorie
(English: Lectures on Number Theory). They were a generalization of the concept of ideal number
s developed by Ernst Kummer
.
Later the concept was expanded by David Hilbert
and especially Emmy Noether
.
, let 
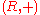be the underlying additive group. A subset 
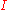is called a two-sided ideal (or simply an ideal) of 
if I is an additive subgroup of R that "absorbs multiplication by elements of R".. Formally we mean that I is an ideal if it satisfies the following conditions:
Equivalently, an ideal of R is a sub-R-bimodule
of R.
A subset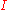
of 
is called a right ideal of 
if it is an additive subgroup of R and absorbs multiplication on the right, that is:
Equivalently, a right ideal of
is a right 
-submodule
of
.
Similarly a subset
of 
is called a left ideal of 
if it is an additive subgroup of R absorbing multiplication on the left:
Equivalently, a left ideal of
is a left 
-submodule of 
.
In all cases, the first condition can be replaced by the following well-known criterion that ensures a nonempty subset of a group is a subgroup:
The left ideals in R are exactly the right ideals in the opposite ring
Ro and vice versa. A two-sided ideal is a left ideal that is also a right ideal, and is often called an ideal except to emphasize that there might exist single-sided ideals. When R is a commutative ring, the definitions of left, right, and two-sided ideal coincide, and the term ideal is used alone.
Just as normal subgroup
s of groups are kernels of group homomorphisms, left/right/two-sided ideals have interpretations as kernels. For a nonempty subset A of R:
If p is in R, then pR is a right ideal and Rp is a left ideal of R. These are called, respectively, the principal
right and left ideals generated by p. To remember which is which, note that right ideals are stable under right-multiplication (IR ⊆ I) and left ideals are stable under left-multiplication (RI ⊆ I).
The connection between cosets and ideals can be seen by switching the operation from "multiplication" to "addition".
We call I a proper ideal if it is a proper subset of R, that is, I does not equal R. The ideal R is called the unit ideal.
But if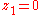
and 
in our new ring, then surely 
should be zero too, and 
as well as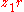 
should be zero for any element r (zero or not).
The definition of an ideal is such that the ideal I generated (see below) by Z is exactly the set of elements that are forced to become zero if Z becomes zero, and the quotient ring
R/I is the desired ring where Z is zero, and only elements that are forced by Z to be zero are zero. The requirement that R and R/I should have the same structure (except that I becomes zero) is formalized by the condition that the projection from R to R/I is a (surjective) ring homomorphism
.
If R is commutative, the left, right, and two-sided ideals generated by a subset X of R are the same, since the left, right, and two-sided ideals of R are the same. We then speak of the ideal of R generated by X, without further specification. However, if R is not commutative they may not be the same.
If R has unity, then the left, right, or two-sided ideal of R generated by a subset X of R can be expressed internally as we will now describe. The following set is a left ideal: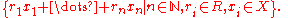
Each element described would have to be in every left ideal containing X, so this left ideal is in fact the left ideal generated by X. The right ideal and ideal generated by X can also be expressed in the same way: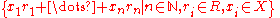
The former is the right ideal generated by X, and the latter is the ideal generated by X.
By convention, 0 is viewed as the sum of zero such terms, agreeing with the fact that the ideal of R generated by ∅ is {0} by the previous definition.
If a left ideal I of R has a finite subset F such that I is the left ideal generated by F, then the left ideal I is said to be finitely generated. Similar terms are also applied to right ideals and two-sided ideals generated by finite subsets.
In the special case where the set X is just a singleton {a} for some a in R, then the above definitions turn into the following:
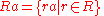
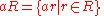
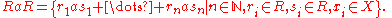
These ideals are known as the left/right/two-sided principal ideal
s generated by a. It is also very common to denote the two-sided ideal generated by a as (a).
If R does not have a unit, then the internal descriptions above must be modified slightly. In addition to the finite sums of products of things in X with things in R, we must allow the addition of n-fold sums of the form x+x+...+x, and n-fold sums of the form (−x)+(−x)+...+(−x) for every x in X and every n in the natural numbers. When R has a unit, this extra requirement becomes superfluous.
Ideals are important because they appear as kernels of ring homomorphisms and allow one to define factor rings. Different types of ideals are studied because they can be used to construct different types of factor rings.
and 
, ideals of a ring R,
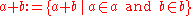
and
i.e. the product of two ideals
and 
is defined to be the ideal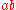 
generated by all products of the form ab with a in 
and b in 
. The product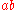 
is contained in
the intersection of
and 
.
The sum and the intersection
of ideals is again an ideal; with these two operations as join and meet, the set of all ideals of a given ring forms a complete
modular lattice
. Also, the union
of two ideals is a subset of the sum of those two ideals, because for any element a inside an ideal, we can write it as a+0, or 0+a, therefore, it is contained in the sum as well. However, the union of two ideals is not necessarily an ideal.
s (equivalence relations that respect the ring structure) on the ring:
Given an ideal I of a ring R, let x ~ y if x-y ∈ I. Then ~ is a congruence relation on R.
Conversely, given a congruence relation ~ on R, let I = {x : x ~ 0}. Then I is an ideal of R.
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
, a branch of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, an ideal is a special subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
. The ideal concept allows the generalization in an appropriate way of some important properties of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s like "even number" or "multiple of 3".
For instance, in rings one studies prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s instead of prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s, one defines coprime ideals as a generalization of coprime numbers
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
, and one can prove a generalized Chinese remainder theorem
Chinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
about ideals. In a certain class of rings important in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the Dedekind domain
Dedekind domain
In abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...
s, one can even recover a version of the fundamental theorem of arithmetic
Fundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
: in these rings, every nonzero ideal can be uniquely written as a product of prime ideals.
An ideal can be used to construct a quotient ring
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
in a similar way as a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
in group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
can be used to construct a quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
. The concept of an order ideal in order theory
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
is derived from the notion of ideal in ring theory.
A fractional ideal
Fractional ideal
In mathematics, in particular commutative algebra, the concept of fractional ideal is introduced in the context of integral domains and is particularly fruitful in the study of Dedekind domains. In some sense, fractional ideals of an integral domain are like ideals where denominators are allowed...
is a generalization of an ideal, and the usual ideals are sometimes called integral ideals for clarity.
History
Ideals were first proposed by Richard DedekindRichard Dedekind
Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
in 1876 in the third edition of his book Vorlesungen über Zahlentheorie
Vorlesungen über Zahlentheorie
' is a textbook of number theory written by German mathematicians Lejeune Dirichlet and Richard Dedekind, and published in 1863....
(English: Lectures on Number Theory). They were a generalization of the concept of ideal number
Ideal number
In number theory an ideal number is an algebraic integer which represents an ideal in the ring of integers of a number field; the idea was developed by Ernst Kummer, and led to Richard Dedekind's definition of ideals for rings...
s developed by Ernst Kummer
Ernst Kummer
Ernst Eduard Kummer was a German mathematician. Skilled in applied mathematics, Kummer trained German army officers in ballistics; afterwards, he taught for 10 years in a gymnasium, the German equivalent of high school, where he inspired the mathematical career of Leopold Kronecker.-Life:Kummer...
.
Later the concept was expanded by David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
and especially Emmy Noether
Emmy Noether
Amalie Emmy Noether was an influential German mathematician known for her groundbreaking contributions to abstract algebra and theoretical physics. Described by David Hilbert, Albert Einstein and others as the most important woman in the history of mathematics, she revolutionized the theories of...
.
Definitions
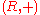For an arbitrary ring, let be the underlying additive group. A subset 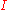is called a two-sided ideal (or simply an ideal) of if I is an additive subgroup of R that "absorbs multiplication by elements of R".. Formally we mean that I is an ideal if it satisfies the following conditions:-
is a subgroupSubgroupIn group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of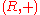
-
-
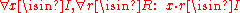
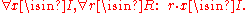
Equivalently, an ideal of R is a sub-R-bimodule
Bimodule
In abstract algebra a bimodule is an abelian group that is both a left and a right module, such that the left and right multiplications are compatible...
of R.
A subset
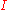of is called a right ideal of if it is an additive subgroup of R and absorbs multiplication on the right, that is:
-
is a subgroup of 
-
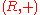
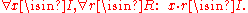
Equivalently, a right ideal of
is a right -submoduleModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
of
.Similarly a subset
of is called a left ideal of if it is an additive subgroup of R absorbing multiplication on the left:
-
is a subgroup of 
-
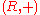
Equivalently, a left ideal of
is a left -submodule of .In all cases, the first condition can be replaced by the following well-known criterion that ensures a nonempty subset of a group is a subgroup:
- 1.' I is non-emptyEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
and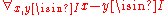
.
The left ideals in R are exactly the right ideals in the opposite ring
Opposite ring
In algebra, the opposite of a ring is another ring with the same elements and addition operation, but with the multiplication performed in the reverse order....
Ro and vice versa. A two-sided ideal is a left ideal that is also a right ideal, and is often called an ideal except to emphasize that there might exist single-sided ideals. When R is a commutative ring, the definitions of left, right, and two-sided ideal coincide, and the term ideal is used alone.
Just as normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
s of groups are kernels of group homomorphisms, left/right/two-sided ideals have interpretations as kernels. For a nonempty subset A of R:
- A is an ideal of R if and only if it is a kernel of a ring homomorphism from R.
- A is a right ideal of R if and only if it is a kernel of a homomorphism from the right R module RR to another right R module.
- A is a left ideal of R if and only if it is a kernel of a homomorphism from the left R module RR to another left R module.
If p is in R, then pR is a right ideal and Rp is a left ideal of R. These are called, respectively, the principal
Principal ideal
In ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
right and left ideals generated by p. To remember which is which, note that right ideals are stable under right-multiplication (IR ⊆ I) and left ideals are stable under left-multiplication (RI ⊆ I).
The connection between cosets and ideals can be seen by switching the operation from "multiplication" to "addition".
We call I a proper ideal if it is a proper subset of R, that is, I does not equal R. The ideal R is called the unit ideal.
Motivation
Intuitively, the definition can be motivated as follows: Suppose we have a subset of elements Z of a ring R and that we would like to obtain a ring with the same structure as R, except that the elements of Z should be zero (they are in some sense "negligible").But if
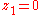and in our new ring, then surely should be zero too, and as well as 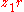should be zero for any element r (zero or not).The definition of an ideal is such that the ideal I generated (see below) by Z is exactly the set of elements that are forced to become zero if Z becomes zero, and the quotient ring
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
R/I is the desired ring where Z is zero, and only elements that are forced by Z to be zero are zero. The requirement that R and R/I should have the same structure (except that I becomes zero) is formalized by the condition that the projection from R to R/I is a (surjective) ring homomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
.
Examples
- The even integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s form an ideal in the ring Z of all integers; it is usually denoted by 2Z. This is because the sum of any even integers is even, and the product of any integer with an even integer is also even. Similarly, the set of all integers divisible by a fixed integer n is an ideal denoted nZ. - The set of all polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s with real coefficients which are divisible by the polynomial x2 + 1 is an ideal in the ring of all polynomials. - The set of all n-by-n matricesMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
whose last row is zero forms a right ideal in the ring of all n-by-n matrices. It is not a left ideal. The set of all n-by-n matrices whose last column is zero forms a left ideal but not a right ideal. - The ring C(R) of all continuous functionContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s f from R to R contains the ideal of all continuous functions f such that f(1) = 0. Another ideal in C(R) is given by those functions which vanish for large enough arguments, i.e. those continuous functions f for which there exists a number L > 0 such that f(x) = 0 whenever |x| > L. - {0} and R are ideals in every ring R. If R is a division ringDivision ringIn abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
or a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, then these are its only ideals. - Compact operatorCompact operatorIn functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
s form an ideal in the ring of bounded operators.
Ideal generated by a set
Let R be a (possibly not unital) ring. Any intersection of any nonempty family of left ideals of R is again a left ideal of R. If X is any subset of R, then the intersection of all left ideals of R containing X is a left ideal I of R containing X, and is clearly the smallest left ideal to do so. This ideal I is said to be the left ideal generated by X. Similar definitions can be created by using right ideals or two-sided ideals in place of left ideals.If R is commutative, the left, right, and two-sided ideals generated by a subset X of R are the same, since the left, right, and two-sided ideals of R are the same. We then speak of the ideal of R generated by X, without further specification. However, if R is not commutative they may not be the same.
If R has unity, then the left, right, or two-sided ideal of R generated by a subset X of R can be expressed internally as we will now describe. The following set is a left ideal:
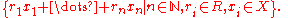
Each element described would have to be in every left ideal containing X, so this left ideal is in fact the left ideal generated by X. The right ideal and ideal generated by X can also be expressed in the same way:
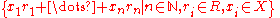
The former is the right ideal generated by X, and the latter is the ideal generated by X.
By convention, 0 is viewed as the sum of zero such terms, agreeing with the fact that the ideal of R generated by ∅ is {0} by the previous definition.
If a left ideal I of R has a finite subset F such that I is the left ideal generated by F, then the left ideal I is said to be finitely generated. Similar terms are also applied to right ideals and two-sided ideals generated by finite subsets.
In the special case where the set X is just a singleton {a} for some a in R, then the above definitions turn into the following:
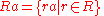
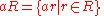
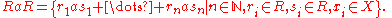
These ideals are known as the left/right/two-sided principal ideal
Principal ideal
In ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
s generated by a. It is also very common to denote the two-sided ideal generated by a as (a).
If R does not have a unit, then the internal descriptions above must be modified slightly. In addition to the finite sums of products of things in X with things in R, we must allow the addition of n-fold sums of the form x+x+...+x, and n-fold sums of the form (−x)+(−x)+...+(−x) for every x in X and every n in the natural numbers. When R has a unit, this extra requirement becomes superfluous.
Example
- In the ring Z of integers, every ideal can be generated by a single number (so Z is a principal ideal domainPrincipal ideal domainIn abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
), and the only two generators of pR are p and −p. The concepts of "ideal" and "number" are therefore almost identical in Z. If aR = bR in an arbitrary domain, then au = b for some unit u. Conversely, for any unit u, aR = auu-1R = auR. So, in a commutative principal ideal domain, the generators of the ideal aR are just the elements au where u is an arbitrary unit. This explains the case of Z since 1 and −1 are the only units of Z.
Types of ideals
- To simplify the description all rings are assumed to be commutative. The non-commutative case is discussed in detail in the respective articles
Ideals are important because they appear as kernels of ring homomorphisms and allow one to define factor rings. Different types of ideals are studied because they can be used to construct different types of factor rings.
- Maximal idealMaximal idealIn mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
: A proper ideal I is called a maximal ideal if there exists no other proper ideal J with I a subset of J. The factor ring of a maximal ideal is a simple ringSimple ringIn abstract algebra, a simple ring is a non-zero ring that has no ideal besides the zero ideal and itself. A simple ring can always be considered as a simple algebra. This notion must not be confused with the related one of a ring being simple as a left module over itself...
in general and is a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
for commutative rings. - Prime idealPrime idealIn algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
: A proper ideal I is called a prime ideal if for any a and b in R, if ab is in I, then at least one of a and b is in I. The factor ring of a prime ideal is a prime ringPrime ringIn abstract algebra, a non-trivial ring R is a prime ring if for any two elements a and b of R, arb = 0 for all r in R implies that either a = 0 or b = 0. Prime ring can also refer to the subring of a field determined by its characteristic...
in general and is an integral domain for commutative rings. - Radical idealRadical of an idealIn commutative ring theory, a branch of mathematics, the radical of an ideal I is an ideal such that an element x is in the radical if some power of x is in I. A radical ideal is an ideal that is its own radical...
or semiprime ideal: A proper ideal I is called radical or semiprime if for any a in R, if an is in I for some n, then a is in I. The factor ring of a radical ideal is a semiprime ringSemiprime ringIn ring theory, semiprime ideals and semiprime rings are generalizations of prime ideals and prime rings. The class of semiprime rings includes semiprimitive rings, prime rings and reduced rings....
for general rings, and is a reduced ringReduced ringIn ring theory, a ring R is called a reduced ring if it has no non-zero nilpotent elements. Equivalently, a ring is reduced if it has no non-zero elements with square zero, that is, x2 = 0 implies x = 0...
for commutative rings. - Primary idealPrimary idealIn mathematics, specifically commutative algebra, a proper ideal Q of a commutative ring A is said to be primary if whenever xy is an element of Q then x or yn is also an element of Q, for some n...
: An ideal I is called a primary ideal if for all a and b in R, if ab is in I, then at least one of a and bn is in I for some natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
n. Every prime ideal is primary, but not conversely. A semiprime primary ideal is prime. - Principal idealPrincipal idealIn ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
: An ideal generated by one element. - Primitive idealPrimitive idealIn mathematics, a left primitive ideal in ring theory is the annihilator of a simple left module. A right primitive ideal is defined similarly. Note that left and right primitive ideals are always two-sided ideals....
: A left primitive ideal is the annihilatorAnnihilator (ring theory)In mathematics, specifically module theory, annihilators are a concept that generalizes torsion and orthogonal complement.-Definitions:Let R be a ring, and let M be a left R-module. Choose a nonempty subset S of M...
of a simpleSimple moduleIn mathematics, specifically in ring theory, the simple modules over a ring R are the modules over R which have no non-zero proper submodules. Equivalently, a module M is simple if and only if every cyclic submodule generated by a non-zero element of M equals M...
left moduleModule (mathematics)In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
. A right primitive ideal is defined similarly. Actually (despite the name) the left and right primitive ideals are always two-sided ideals. Primitive ideals are prime. A factor rings constructed with a right (left) primitive ideals is a right (left) primitive ringPrimitive ringIn the branch of abstract algebra known as ring theory, a left primitive ring is a ring which has a faithful simple left module. Well known examples include endomorphism rings of vector spaces and Weyl algebras over fields of characteristic zero.- Definition :...
. For commutative rings the primitive ideals are maximal, and so commutative primitive rings are all fields. - Irreducible idealIrreducible idealIn mathematics, an ideal of a commutative ring is said to be irreducible if it cannot be written as a finite intersection of ideals properly containing it....
: An ideal is said to be irreducible if it cannot be written as an intersection of ideals which properly contain it. - Comaximal ideals: Two ideals
are said to be comaximal if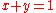 
for some 
and 
.
Properties
- An ideal is proper if and only if it does not contain 1.
- The proper ideals can be partially orderedPartially ordered setIn mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
via subset inclusionSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
and therefore as a consequence of Zorn's lemmaZorn's lemmaZorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory that states:Suppose a partially ordered set P has the property that every chain has an upper bound in P...
every proper ideal is contained in a maximal ideal. - Because zero belongs to it, any ideal is nonempty.
- The ring R can be considered as a left module over itself, and the left ideals of R are then seen as the submodules of this module. Similarly, the right ideals are submodules of R as a right module over itself, and the two-sided ideals are submodules of R as a bimoduleBimoduleIn abstract algebra a bimodule is an abelian group that is both a left and a right module, such that the left and right multiplications are compatible...
over itself. If R is commutative, then all three sorts of module are the same, just as all three sorts of ideal are the same. - Every ideal is a pseudo-ring.
- The ideals of a ring form a semiringSemiringIn abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
under addition and multiplication of ideals.
Ideal operations
The sum and product of ideals are defined as follows. For and , ideals of a ring R,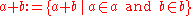and
i.e. the product of two ideals
and is defined to be the ideal 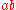generated by all products of the form ab with a in and b in . The product 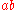is contained inSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
the intersection of
and .The sum and the intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of ideals is again an ideal; with these two operations as join and meet, the set of all ideals of a given ring forms a complete
Complete lattice
In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...
modular lattice
Modular lattice
In the branch of mathematics called order theory, a modular lattice is a lattice that satisfies the following self-dual condition:Modular law: x ≤ b implies x ∨ = ∧ b,where ≤ is the partial order, and ∨ and ∧ are...
. Also, the union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of two ideals is a subset of the sum of those two ideals, because for any element a inside an ideal, we can write it as a+0, or 0+a, therefore, it is contained in the sum as well. However, the union of two ideals is not necessarily an ideal.
Ideals and congruence relations
There is a bijective correspondence between ideals and congruence relationCongruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
s (equivalence relations that respect the ring structure) on the ring:
Given an ideal I of a ring R, let x ~ y if x-y ∈ I. Then ~ is a congruence relation on R.
Conversely, given a congruence relation ~ on R, let I = {x : x ~ 0}. Then I is an ideal of R.
See also
- Modular arithmeticModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
- Noether isomorphism theorem
- Boolean prime ideal theoremBoolean prime ideal theoremIn mathematics, a prime ideal theorem guarantees the existence of certain types of subsets in a given abstract algebra. A common example is the Boolean prime ideal theorem, which states that ideals in a Boolean algebra can be extended to prime ideals. A variation of this statement for filters on...
- Ideal theoryIdeal theoryIn mathematics, ideal theory is the theory of ideals in commutative rings; and is the precursor name for the contemporary subject of commutative algebra...
- Ideal (order theory)Ideal (order theory)In mathematical order theory, an ideal is a special subset of a partially ordered set . Although this term historically was derived from the notion of a ring ideal of abstract algebra, it has subsequently been generalized to a different notion...
- Ideal quotient
- Norm of an idealNorm of an idealIn commutative algebra, the norm of an ideal is a generalization of a norm of an element in the field extension. It is particularly important in number theory since it measures the size of an ideal of a complicated number ring in terms of an ideal in a less complicated ring...
- Artinian idealArtinian idealIn abstract algebra, an Artinian ideal, named after Emil Artin, is encountered in ring theory, in particular, with polynomial rings.Given a polynomial ring R = k[X1, ... Xn] where k is some field, an Artinian ideal is an ideal I in R for which the Krull dimension of the quotient...
- Noncommutative ringNoncommutative ringIn mathematics, more specifically modern algebra and ring theory, a noncommutative ring is a ring whose multiplication is not commutative; that is, if R is a noncommutative ring, there exists a and b in R with a·b ≠ b·a, and conversely.Noncommutative rings are ubiquitous in mathematics, and occur...
- Regular ideal
- IdealizerIdealizerIn mathematics, the idealizer R of an additive subgroup A of a ring R is the largest subring of R that contains A as a two-sided ideal...