Blackboard bold is a typeface

Typeface

In typography, a typeface is the artistic representation or interpretation of characters; it is the way the type looks. Each type is designed and there are thousands of different typefaces in existence, with new ones being developed constantly....

 style that is often used for certain symbols in mathematical

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

 texts, in which certain lines of the symbol (usually vertical or near-vertical lines) are doubled. The symbols usually denote number sets. Blackboard bold symbols are also referred to as double struck, although they cannot actually be produced by double striking on a typewriter

Typewriter

A typewriter is a mechanical or electromechanical device with keys that, when pressed, cause characters to be printed on a medium, usually paper. Typically one character is printed per keypress, and the machine prints the characters by making ink impressions of type elements similar to the pieces...

.

Chicago Manual of Style in 1993 (14th edition) advices: "[b]lackboard bold should be confined to the classroom" (13.14) whereas in 2003 (15th edition) they agree that "[o]pen-faced (blackboard) symbols are reserved for familiar systems of numbers" (14.12).

In some texts these symbols are simply shown in bold type: blackboard bold in fact originated from the attempt to write bold letters on blackboard

Chalkboard

A chalkboard or blackboard is a reusable writing surface on which text or drawings are made with sticks of calcium sulfate or calcium carbonate, known, when used for this purpose, as chalk. Chalkboards were originally made of smooth, thin sheets of black or dark grey slate stone...

s in a way that clearly differentiated them from non-bold letters, and then made its way back in print form as a separate style from ordinary bold, possibly starting with the original 1965 edition of Gunning

Robert Gunning (mathematician)

Robert Clifford Gunning is a professor of mathematics at Princeton University specializing in complex analysis. He joined the faculty in 1956 and was dean of the faculty from 1989 to 1995. He was Salomon Bochner's dissertation student.-External links:*...

 and Rossi's textbook on complex analysis. Some mathematicians, therefore, do not recognize blackboard bold as a separate style from bold: Jean-Pierre Serre

Jean-Pierre Serre

Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...

, for example, has publicly inveighed against the use of "blackboard bold" anywhere other than on a blackboard, and uses double-struck letters when writing bold on the blackboard, whereas his published works consistently use ordinary bold for the same symbols. It is sometimes erroneously claimed that Bourbaki introduced the blackboard bold notation, but whereas individual members of the Bourbaki group may have popularized double-striking bold characters on the blackboard, their printed books use ordinary bold.

The symbols are nearly universal in their interpretation, unlike their normally-typeset counterparts, which are used for many different purposes.

TeX

TeX

TeX is a typesetting system designed and mostly written by Donald Knuth and released in 1978. Within the typesetting system, its name is formatted as ....

, the standard typesetting system for mathematical texts, does not contain direct support for blackboard bold symbols, but the add-on AMS Fonts package (amsfonts) by the American Mathematical Society

American Mathematical Society

The American Mathematical Society is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, which it does with various publications and conferences as well as annual monetary awards and prizes to mathematicians.The society is one of the...

 provides this facility; a blackboard bold R is written as \mathbb{R}.

In Unicode

Unicode

Unicode is a computing industry standard for the consistent encoding, representation and handling of text expressed in most of the world's writing systems...

, a few of the more common blackboard bold characters (C, H, N, P, Q, R and Z) are encoded in the Basic Multilingual Plane (BMP) in the Letterlike Symbols (2100–214F) area, named DOUBLE-STRUCK CAPITAL C etc. The rest, however, are encoded outside the BMP, from U+1D538 to U+1D550 (uppercase, excluding those encoded in the BMP), U+1D552 to U+1D56B (lowercase) and U+1D7D8 to U+1D7E1 (digits). Being outside the BMP, these are relatively new and not widely supported.

Examples

The following table shows all available Unicode blackboard bold characters.

The first column shows the letter as typically rendered by the ubiquitous LaTeX

LaTeX

LaTeX is a document markup language and document preparation system for the TeX typesetting program. Within the typesetting system, its name is styled as . The term LaTeX refers only to the language in which documents are written, not to the editor used to write those documents. In order to...

 markup system. The second column shows the Unicode codepoint. The third column shows the symbol itself (which will only display correctly if your browser supports Unicode and has access to a suitable font). The fourth column describes known typical (but not universal) usage in mathematical texts.

	Unicode (Hex)	Symbol	Mathematics usage
	U+1D538		Represents affine space Affine space In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...  or the ring of adeles Adele ring In algebraic number theory and topological algebra, the adele ring is a topological ring which is built on the field of rational numbers . It involves all the completions of the field.... . Sometimes represents the algebraic number Algebraic number In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental... s, the algebraic closure Algebraic closure In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....  of Q ( or , although Q is often used instead). It may also represent the algebraic integer Algebraic integer In number theory, an algebraic integer is a complex number that is a root of some monic polynomial with coefficients in . The set of all algebraic integers is closed under addition and multiplication and therefore is a subring of complex numbers denoted by A... s, an important subring of the algebraic numbers.
	U+1D552
	U+1D539		Sometimes represents a ball Ball (mathematics) In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball .... , a boolean domain Boolean domain In mathematics and abstract algebra, a Boolean domain is a set consisting of exactly two elements whose interpretations include false and true... , or the Brauer group Brauer group In mathematics, the Brauer group of a field K is an abelian group whose elements are Morita equivalence classes of central simple algebras of finite rank over K and addition is induced by the tensor product of algebras. It arose out of attempts to classify division algebras over a field and is...  of a field.
	U+1D553
	U+2102		Represents the complex number Complex number A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part... s.
	U+1D554
	U+1D53B		Represents the unit (open Open - Philosophy :* Openness, term being used to define the basis of how various groups and organizations operate- Mathematics :* Open problem, a well-defined problem with no known solution in science and mathematics... ) disk in the complex plane Complex plane In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...  (for example as a model of the Hyperbolic plane Hyperbolic geometry In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced... ), or the decimal fractions (see number Number A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers.... ).
	U+1D555
	U+2145
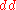	U+2146		May represent the differential Differential (calculus) In calculus, a differential is traditionally an infinitesimally small change in a variable. For example, if x is a variable, then a change in the value of x is often denoted Δx . The differential dx represents such a change, but is infinitely small...  symbol.
	U+1D53C		Represents the expected value Expected value In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...  of a random variable Random variable In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable... , or Euclidean space Euclidean space In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions... , or a field Field (mathematics) In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...  in a tower of fields.
	U+1D556
	U+2147		Sometimes used for the mathematical constant e E (mathematical constant) The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base... .
	U+1D53D		Represents a field Field (mathematics) In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms... . Often used for finite field Finite field In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory... s, with a subscript to indicate the order. Also represents a Hirzebruch surface Hirzebruch surface In mathematics, a Hirzebruch surface is a ruled surface over the projective line. They were studied by .-Definition:The Hirzebruch surfaceΣn is the P1 bundle over P1associated to the sheafO+O.\...  or a free group Free group In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses... , with a subset to indicate the number of generators (or generating set, if infinite).
	U+1D557
	U+1D53E		Represents a Grassmannian Grassmannian In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...  or a group Group (mathematics) In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity... , especially an algebraic group Algebraic group In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety... .
	U+1D558
	U+210D		Represents the quaternions (the H stands for Hamilton William Rowan Hamilton Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques... ), or the upper half-plane, or hyperbolic space Hyperbolic space In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point... , or hyperhomology Hyperhomology In homological algebra, the hyperhomology or hypercohomology of a complexof objects of an abelian category is an extension of the usual homology of an object to complexes....  of a complex.
	U+1D559
	U+1D540		Occasionally used to denote the identity mapping Identity function In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...  on an algebraic structure Algebraic structure In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties... , or the set of imaginary number Imaginary number An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative... s (i.e., the set of all real multiples of the imaginary unit Imaginary unit In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek... ).
	U+1D55A
	U+2148		Occasionally used for the imaginary unit Imaginary unit In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek... .
	U+1D541		Sometimes represents the irrational number Irrational number In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number.... s, R\Q .
	U+1D541
	U+2149
	U+1D542		Represents a field Field (mathematics) In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms... . This is derived from the German German language German is a West Germanic language, related to and classified alongside English and Dutch. With an estimated 90 – 98 million native speakers, German is one of the world's major languages and is the most widely-spoken first language in the European Union....  word Körper, which is German for field (literally, "body"; cf. the French term corps). May also be used to denote a compact space Compact space In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces... .
	U+1D55C
	U+1D543		Represents the Lefschetz motive. See motives Motive (algebraic geometry) In algebraic geometry, a motive denotes 'some essential part of an algebraic variety'. To date, pure motives have been defined, while conjectural mixed motives have not. Pure motives are triples , where X is a smooth projective variety, p : X ⊢ X is an idempotent correspondence, and m an integer... .
	U+1D55D
	U+1D544
	U+1D55E
	U+2115		Represents the natural number Natural number In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively... s. May or may not include zero 0 (number) 0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems... .
	U+1D55F
	U+1D546		Represents the octonion Octonion In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H... s.
	U+1D560
	U+2119		Represents projective space Projective space In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively.... , the probability Probability Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...  of an event, the prime number Prime number A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2... s, a power set, the positive reals, the irrational numbers, or a forcing Forcing (mathematics) In the mathematical discipline of set theory, forcing is a technique invented by Paul Cohen for proving consistency and independence results. It was first used, in 1963, to prove the independence of the axiom of choice and the continuum hypothesis from Zermelo–Fraenkel set theory...  partially ordered set Partially ordered set In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...  (poset).
	U+1D561
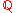	U+211A		Represents the rational number Rational number In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number... s. (The Q stands for quotient Quotient In mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A... .)
	U+1D562
	U+211D		Represents the real number Real number In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π... s.
	U+1D563
	U+1D54A		Represents the sedenion Sedenion In abstract algebra, sedenions form a 16-dimensional non-associative algebra over the reals obtained by applying the Cayley–Dickson construction to the octonions... s, or a sphere Sphere A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point... .
	U+1D564
	U+1D54B		Represents a torus Torus In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle... , or the circle group or a Hecke algebra Hecke algebra In mathematics, the Iwahori–Hecke algebra, or Hecke algebra, named for Erich Hecke and Nagayoshi Iwahori, is a one-parameter deformation of the group algebra of a Coxeter group....  (Hecke denoted his operators as Tn or ).
	U+1D565
	U+1D54C
	U+1D566
	U+1D54D		Represents a vector space Vector space A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex... .
	U+1D567
	U+1D54E		Represents the whole number Whole number Whole number is a term with inconsistent definitions by different authors. All distinguish whole numbers from fractions and numbers with fractional parts.Whole numbers may refer to:*natural numbers in sense — the positive integers... s (here in the sense of non-negative integers), which also are represented by N0.
	U+1D568
	U+1D54F		Occasionally used to denote an arbitrary metric space Metric space In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space... .
	U+1D569
	U+1D550
	U+1D56A
	U+2124		Represents the integer Integer The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively... s. (The Z is for Zahlen, which is German for "numbers".)
	U+1D56B
	U+213E
	U+213D
	U+213F
	U+213C
	U+2140
	U+1D7D8
	U+1D7D9		Often represents, in set theory Set theory Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics... , the top element Greatest element In mathematics, especially in order theory, the greatest element of a subset S of a partially ordered set is an element of S which is greater than or equal to any other element of S. The term least element is defined dually...   of a forcing partially ordered set Partially ordered set In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...  (poset), or occasionally for the identity matrix in a matrix ring Matrix ring In abstract algebra, a matrix ring is any collection of matrices forming a ring under matrix addition and matrix multiplication. The set of n×n matrices with entries from another ring is a matrix ring, as well as some subsets of infinite matrices which form infinite matrix rings... .
	U+1D7DA
	U+1D7DB
	U+1D7DC
	U+1D7DD
	U+1D7DE
	U+1D7DF
	U+1D7E0
	U+1D7E1

A blackboard bold Greek letter mu (not found in Unicode) is sometimes used by number theorists and algebraic geometers (with a subscript n) to designate the group (or more specifically group scheme

Group scheme

In mathematics, a group scheme is a type of algebro-geometric object equipped with a composition law. Group schemes arise naturally as symmetries of schemes, and they generalize algebraic groups, in the sense that all algebraic groups have group scheme structure, but group schemes are not...

) of n-th roots of unity

Root of unity

In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...

.

Another option is to use the amssymb package. This will output a and in your document.
{|border="0" cellpadding="0" cellspacing="1em"
|
\usepackage{amssymb}
...
\mathbb{R}
\mathbb{Z}

External links

• http://www.w3.org/TR/MathML2/double-struck.html shows blackboard bold symbols together with their Unicode encodings. Encodings in the Basic Multilingual Plane are highlighted in yellow.