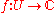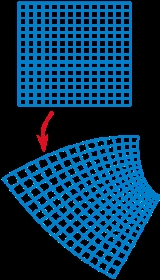
Conformal map
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a conformal map is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
which preserves angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
s. In the most common case the function is between domains in the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
.
More formally, a map,
is called conformal (or angle-preserving) at
 if it preserves oriented angles between curve
if it preserves oriented angles between curveCurve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s through
 with respect to their orientation
with respect to their orientationOrientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
(i.e., not just the acute angle). Conformal maps preserve both angles and the shapes of infinitesimally small figures, but not necessarily their size.
The conformal property may be described in terms of the Jacobian derivative matrix of a coordinate transformation. If the Jacobian matrix of the transformation is everywhere a scalar times a rotation matrix, then the transformation is conformal.
Conformal maps can be defined between domains in higher dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
s, and more generally on a Riemannian
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
or semi-Riemannian manifold.
Complex analysis
An important family of examples of conformal maps comes from complex analysisComplex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
. If U is an open subset
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
of the complex plane,
 , then a function
, then a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
is conformal if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is holomorphic
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
and its derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
is everywhere non-zero on U. If f is antiholomorphic
Antiholomorphic function
In mathematics, antiholomorphic functions are a family of functions closely related to but distinct from holomorphic functions....
(that is, the conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
to a holomorphic function), it still preserves angles, but it reverses their orientation.
The Riemann mapping theorem, one of the profound results of complex analysis, states that any non-empty open simply connected proper subset of
 admits a bijective
admits a bijectiveBijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
conformal map to the open unit disk in
 .
.A map of the extended complex plane
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
(which is conformally equivalent to a sphere) onto itself is conformal if and only if it is a Möbius transformation. Again, for the conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
, angles are preserved, but orientation is reversed.
An example of the latter is taking the reciprocal of the conjugate, which corresponds to circle inversion with respect to the unit circle. This can also be expressed as taking the reciprocal of the radial coordinate in circular coordinates, keeping the angle the same. See also inversive geometry.
Riemannian geometry
In Riemannian geometryRiemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, two Riemannian metrics
 and
and  on smooth manifold
on smooth manifold  are called conformally equivalent if
are called conformally equivalent if 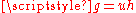 for some positive function
for some positive function  on
on  . The function
. The function  is called the conformal factor.
is called the conformal factor.A diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
between two Riemannian manifolds is called a conformal map if the pulled back metric is conformally equivalent to the original one. For example, stereographic projection
Stereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
of a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
onto the plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
augmented with a point at infinity is a conformal map.
One can also define a conformal structure on a smooth manifold, as a class of conformally equivalent Riemannian metrics.
Higher-dimensional Euclidean space
A classical theorem of Joseph LiouvilleJoseph Liouville
- Life and work :Liouville graduated from the École Polytechnique in 1827. After some years as an assistant at various institutions including the Ecole Centrale Paris, he was appointed as professor at the École Polytechnique in 1838...
called Liouville's theorem shows the higher-dimensions have less varied conformal maps:
Any conformal map on a portion of Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
of dimension greater than 2 can be composed from three types of transformation: a homothetic transformation, an isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
, and a special conformal transformation. (A special conformal transformation is the composition of a reflection and an inversion in a sphere
Inversion (geometry)
In geometry, inversive geometry is the study of those properties of figures that are preserved by a generalization of a type of transformation of the Euclidean plane, called inversion...
.) Thus, the group of conformal transformations in spaces of dimension greater than 2 are much more restricted than the planar case, where the Riemann mapping theorem provides a large group of conformal transformations.
Uses
If a function is harmonicHarmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
(that is, it satisfies Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
 ) over a particular space, and is transformed via a conformal map to another space, the transformation is also harmonic. For this reason, any function which is defined by a potential
) over a particular space, and is transformed via a conformal map to another space, the transformation is also harmonic. For this reason, any function which is defined by a potentialPotential
*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
can be transformed by a conformal map and still remain governed by a potential. Examples in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
of equations defined by a potential include the electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
, the gravitational field
Gravitational field
The gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
, and, in fluid dynamics
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, potential flow
Potential flow
In fluid dynamics, potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications...
, which is an approximation to fluid flow assuming constant density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
, zero viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
, and irrotational flow
Irrotational vector field
In vector calculus a conservative vector field is a vector field which is the gradient of a function, known in this context as a scalar potential. Conservative vector fields have the property that the line integral from one point to another is independent of the choice of path connecting the two...
. One example of a fluid dynamic application of a conformal map is the Joukowsky transform
Joukowsky transform
In applied mathematics, the Joukowsky transform, named after Nikolai Zhukovsky, is a conformal map historically used to understand some principles of airfoil design.The transform is...
.
Conformal mappings are invaluable for solving problems in engineering and physics that can be expressed in terms of functions of a complex variable but that exhibit inconvenient geometries. By choosing an appropriate mapping, the analyst can transform the inconvenient geometry into a much more convenient one. For example, one may wish to calculate the electric field,
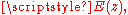 arising from a point charge located near the corner of two conducting planes separated by a certain angle (where
arising from a point charge located near the corner of two conducting planes separated by a certain angle (where  is the complex coordinate of a point in 2-space). This problem per se is quite clumsy to solve in closed form. However, by employing a very simple conformal mapping, the inconvenient angle is mapped to one of precisely pi radians, meaning that the corner of two planes is transformed to a straight line. In this new domain, the problem (that of calculating the electric field impressed by a point charge located near a conducting wall) is quite easy to solve. The solution is obtained in this domain,
is the complex coordinate of a point in 2-space). This problem per se is quite clumsy to solve in closed form. However, by employing a very simple conformal mapping, the inconvenient angle is mapped to one of precisely pi radians, meaning that the corner of two planes is transformed to a straight line. In this new domain, the problem (that of calculating the electric field impressed by a point charge located near a conducting wall) is quite easy to solve. The solution is obtained in this domain, 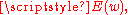 and then mapped back to the original domain by noting that
and then mapped back to the original domain by noting that  was obtained as a function (viz., the composition
was obtained as a function (viz., the compositionFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
of
 and
and  ) of
) of  whence
whence 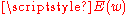 can be viewed as
can be viewed as  which is a function of
which is a function of  the original coordinate basis. Note that this application is not a contradiction to the fact that conformal mappings preserve angles, they do so only for points in the interior of their domain, and not at the boundary.
the original coordinate basis. Note that this application is not a contradiction to the fact that conformal mappings preserve angles, they do so only for points in the interior of their domain, and not at the boundary.A large group of conformal maps for relating solutions of Maxwell’s equations was identified by Ebenezer Cunningham
Ebenezer Cunningham
Ebenezer Cunningham was a British mathematician who is remembered for his research and exposition at the dawn of special relativity....
(1908) and Harry Bateman
Harry Bateman
Harry Bateman FRS was an English mathematician.-Life and work:Harry Bateman first grew to love mathematics at Manchester Grammar School, and in his final year, won a scholarship to Trinity College, Cambridge. There he distinguished himself in 1903 as Senior Wrangler and by winning the Smith's Prize...
(1910). Their training at Cambridge University had given them facility with the method of image charges
Method of image charges
The method of image charges is a basic problem-solving tool in electrostatics...
and associated methods of images for spheres and inversion. As recounted by Andrew Warwick (2003) Masters of Theory:
- Each four-dimensional solution could be inverted in a four-dimensional hyper-sphere of pseudo-radius K in order to produce a new solution.
Warwick highlights (pages 404 to 424) this "new theorem of relativity" as a Cambridge response to Einstein, and as founded on exercises using the method of inversion, such as found in James Hopwood Jeans
James Hopwood Jeans
Sir James Hopwood Jeans OM FRS MA DSc ScD LLD was an English physicist, astronomer and mathematician.-Background:...
textbook Mathematical Theory of Electricity and Magnetism.
In cartography
Cartography
Cartography is the study and practice of making maps. Combining science, aesthetics, and technique, cartography builds on the premise that reality can be modeled in ways that communicate spatial information effectively.The fundamental problems of traditional cartography are to:*Set the map's...
, several named map projections (including the Mercator projection) are conformal.
In General Relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, conformal maps are the simplest and thus most common type of causal transformations. Physically, these describe different universes in which all the same events and interactions are still (causally) possible, but a new additional force is necessary to effect this (that is, replication of all the same trajectories would necessitate departures from geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
motion because the metric
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
is different). It is often used to try to make models amenable to extension beyond curvature singularities
Gravitational singularity
A gravitational singularity or spacetime singularity is a location where the quantities that are used to measure the gravitational field become infinite in a way that does not depend on the coordinate system...
, for example to permit description of the universe even before the big bang
Big Bang
The Big Bang theory is the prevailing cosmological model that explains the early development of the Universe. According to the Big Bang theory, the Universe was once in an extremely hot and dense state which expanded rapidly. This rapid expansion caused the young Universe to cool and resulted in...
.
Alternative angles
A conformal map is called that because it conforms to the principle of angle-preservation. The presumption often is that the angle being preserved is the standard Euclidean angleAngle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
, say parameterized in degrees or radians. However, in plane mapping there are two other angles to consider: the hyperbolic angle
Hyperbolic angle
In mathematics, a hyperbolic angle is a geometric figure that divides a hyperbola. The science of hyperbolic angle parallels the relation of an ordinary angle to a circle...
and the slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
, which is the analogue of angle for dual numbers.
Suppose
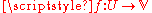 is a mapping of surfaces parameterized by
is a mapping of surfaces parameterized by 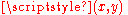 and
and 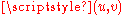 . The Jacobian matrix of
. The Jacobian matrix of  is formed by the four partial derivative
is formed by the four partial derivativePartial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s of
 and
and  with respect to
with respect to  and
and  .
.If the Jacobian g has a non-zero determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
, then
 is "conformal in the generalized sense" with respect to one of the three angle types, depending on the real matrix expressed by the Jacobian g.
is "conformal in the generalized sense" with respect to one of the three angle types, depending on the real matrix expressed by the Jacobian g.Indeed, any such g lies in a particular planar commutative subring
Subring
In mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
, and g has a polar coordinate form determined by parameters of radial and angular nature. The radial parameter corresponds to a similarity mapping
Similarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
and can be taken as 1 for purposes of conformal examination. The angular parameter of g is one of the three types, shear, hyperbolic, or Euclidean:
- When the subring is isomorphic to the dual numberDual numberIn linear algebra, the dual numbers extend the real numbers by adjoining one new element ε with the property ε2 = 0 . The collection of dual numbers forms a particular two-dimensional commutative unital associative algebra over the real numbers. Every dual number has the form z = a + bε with a and...
plane, then g acts as a shear mapping and preserves the dual angle. - When the subring is isomorphic to the split-complex numberSplit-complex numberIn abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...
plane, then g acts as a squeeze mappingSqueeze mappingIn linear algebra, a squeeze mapping is a type of linear map that preserves Euclidean area of regions in the Cartesian plane, but is not a Euclidean motion.For a fixed positive real number r, the mapping →...
and preserves the hyperbolic angle. - When the subring is isomorphic to the ordinary complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
plane, then g acts as a rotationRotationA rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
and preserves the Euclidean angle.
While describing analytic functions of a bireal variable, U. Bencivenga and G. Fox have written about conformal maps that preserve the hyperbolic angle.
See also
- Conformal picturesConformal picturesHere are examples of conformal maps understood as deforming pictures. This technique is a generalization of domain coloring where the domain space is not colored by a fixed infinite color wheel but by a finite picture tiling the plane...
- Schwarz–Christoffel mapping
- Penrose diagramPenrose diagramIn theoretical physics, a Penrose diagram is a two-dimensional diagram that captures the causal relations between different points in spacetime...
- Carathéodory's theoremCarathéodory's theorem (conformal mapping)In mathematical complex analysis, Carathéodory's theorem, proved by , states that if U is a simply connected open subset of the complex plane C, whose boundary is a Jordan curve Γ then the Riemann map...
External links
- Conformal Mapping Module by John H. Mathews
- interactive visualizations of many conformal maps
- Conformal Maps by Michael Trott, Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
. - Java applet by Jürgen Richter-Gebert using CinderellaCinderella (software)Cinderella is a proprietary interactive geometry software, written in Java programming language.- History :Cinderella was initially developed by Jürgen Richter-Gebert and Henry Crapo and was used to input incidence theorems and conjectures for automatic theorem proving using the binomial proving...
. - Java applet by Christian Mercat to deform pictures; MacOSX Java applet that deforms the video flux from the webcam.
- Conformal Mapping images of current flow in different geometries without and with magnetic field by Gerhard Brunthaler.