
Injective function
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
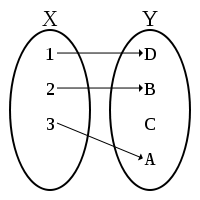
, an injective function is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
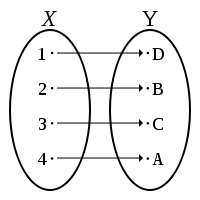
. In other words, every element of the function's codomain is mapped to by at most one element of its domain. If in addition all of the elements in the codomain are in fact mapped to by some element of the domain, then the function is said to be bijective (see figures).
An injective function is called an injection, and is also said to be a one-to-one function (not to be confused with one-to-one correspondence, i.e. a bijective function). Occasionally, an injective function from X to Y is denoted , using an arrow with a barbed tail. The set of injective functions from X to Y may be denoted YX using a notation derived from that used for falling factorial powers, since if X and Y are finite sets with respectively m and n elements, the number of injections from X to Y is nm (see the twelvefold way).
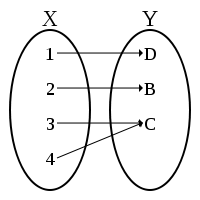
A function f that is not injective is sometimes called many-to-one. (However, this terminology is also sometimes used to mean "single-valued", i.e., each argument is mapped to at most one value; this is the case for any function, but is used to stress the opposition with multi-valued functions, which are not true functions.)
A monomorphism
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
is a generalization of an injective function in category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
.
Definition
Let f be a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
whose domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
is a set A. The function f is injective if for all a and b in A, if f(a) = f(b), then a = b; that is, f(a) = f(b) implies a = b. Equivalently, if a ≠ b, then f(a) ≠ f(b).
Examples
- For any set X and any subset S of X the inclusion mapInclusion mapIn mathematics, if A is a subset of B, then the inclusion map is the function i that sends each element, x of A to x, treated as an element of B:i: A\rightarrow B, \qquad i=x....
(which sends any element s of S to itself) is injective. In particular the identity functionIdentity functionIn mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
is always injective (and in fact bijective). - If the domain X = ∅ or X has only one element, the function is always injective.
- The function f : R → R defined by f(x) = 2x + 1 is injective.
- The function g : R → R defined by g(x) = x2 is not injective, because (for example) g(1) = 1 = g(−1). However, if g is redefined so that its domain is the non-negative real numbers
[0,+∞) , then g is injective. - The exponential functionExponential functionIn mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
exp : R → R defined by exp(x) = ex is injective (but not surjective as no real value maps to a negative number). - The natural logarithmNatural logarithmThe natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
function ln : (0, ∞) → R defined by x ↦ ln x is injective. - The function g : R → R defined by g(x) = xn − x is not injective, since, for example, g(0) = g(1).
More generally, when X and Y are both the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
R, then an injective function f : R → R is one whose graph is never intersected by any horizontal line more than once. This principle is referred to as the horizontal line test
Horizontal line test
In mathematics, the horizontal line test is a test used to determine if a function is injective and/or surjective.The lines used for the test are parallel to the x axis....
.
Injections can be undone
Functions with left inverses are always injections. That is, given f : X → Y, if there is a function g : Y → X such that, for every x ∈ X- g(f(x)) = x (f can be undone by g)
then f is injective. In this case, f is called a section of g and g is called a retraction of f.
Conversely, every injection f with non-empty domain has a left inverse g (in conventional mathematics). Note that g may not be a complete inverse
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
of f because the composition in the other order, f ∘ g, may not be the identity on Y. In other words, a function that can be undone or "reversed", such as f, is not necessarily invertible
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
(bijective). Injections are "reversible" but not always invertible.
Although it is impossible to reverse a non-injective (and therefore information-losing) function, one can at least obtain a "quasi-inverse" of it, that is a multiple-valued
Multivalued function
In mathematics, a multivalued function is a left-total relation; i.e. every input is associated with one or more outputs...
function.
Injections may be made invertible
In fact, to turn an injective function f : X → Y into a bijective (hence invertibleInverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
) function, it suffices to replace its codomain Y by its actual range J = f(X). That is, let g : X → J such that g(x) = f(x) for all x in X; then g is bijective. Indeed, f can be factored as inclJ,Y ∘ g, where inclJ,Y is the inclusion function from J into Y.
Other properties
- If f and g are both injective, then f ∘ g is injective.

- If g ∘ f is injective, then f is injective (but g need not be).
- f : X → Y is injective if and only if, given any functions g, h : W → X, whenever f ∘ g = f ∘ h, then g = h. In other words, injective functions are precisely the monomorphismMonomorphismIn the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
s in the categoryCategory theoryCategory theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
SetCategory of setsIn the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
of sets. - If f : X → Y is injective and A is a subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of X, then f −1(f(A)) = A. Thus, A can be recovered from its image f(A). - If f : X → Y is injective and A and B are both subsets of X, then f(A ∩ B) = f(A) ∩ f(B).
- Every function h : W → Y can be decomposed as h = f ∘ g for a suitable injection f and surjection g. This decomposition is unique up to isomorphism, and f may be thought of as the inclusion function of the range h(W) of h as a subset of the codomain Y of h.
- If f : X → Y is an injective function, then Y has at least as many elements as X, in the sense of cardinal numberCardinal numberIn mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
s. In particular, if, in addition, there is an injection from to
to  , then
, then  and
and  have the same cardinal number. (This is known as the Cantor–Bernstein–Schroeder theoremCantor–Bernstein–Schroeder theoremIn set theory, the Cantor–Bernstein–Schroeder theorem, named after Georg Cantor, Felix Bernstein, and Ernst Schröder, states that, if there exist injective functions and between the sets A and B, then there exists a bijective function...
have the same cardinal number. (This is known as the Cantor–Bernstein–Schroeder theoremCantor–Bernstein–Schroeder theoremIn set theory, the Cantor–Bernstein–Schroeder theorem, named after Georg Cantor, Felix Bernstein, and Ernst Schröder, states that, if there exist injective functions and between the sets A and B, then there exists a bijective function...
.) - If both X and Y are finite with the same number of elements, then f : X → Y is injective if and only if f is surjective (in which case f is bijective).
- An injective function which is a homomorphismHomomorphismIn abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
between two algebraic structures is an embeddingEmbeddingIn mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
. - Unlike surjectivity, which is a relation between the graph of a function and its codomain, injectivity is a property of the graph of the function alone; that is, whether a function f is injective can be decided by only considering the graph (and not the codomain) of f.
See also
- Surjective functionSurjective functionIn mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
- Bijective function
- Injective moduleInjective moduleIn mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module Q that shares certain desirable properties with the Z-module Q of all rational numbers...
- Bijection, injection and surjectionBijection, injection and surjectionIn mathematics, injections, surjections and bijections are classes of functions distinguished by the manner in which arguments and images are related or mapped to each other.A function maps elements from its domain to elements in its codomain.*A function f: \; A \to B is injective...
- Horizontal line testHorizontal line testIn mathematics, the horizontal line test is a test used to determine if a function is injective and/or surjective.The lines used for the test are parallel to the x axis....
- Injective metric spaceInjective metric spaceIn metric geometry, an injective metric space, or equivalently a hyperconvex metric space, is a metric space with certain properties generalizing those of the real line and of L∞ distances in higher-dimensional vector spaces...

