Quaternion variable
Encyclopedia
In mathematics
, a function of a quaternion variable is a function
with domain and range
in the quaternions H.
The projections
of a quaternion onto its scalar part or onto its vector part, as well as the modulus and versor functions, are examples that are basic to understanding quaternion structure. A very useful function of a quaternion variable is
which rotates the vector part of q
by twice the angle of u.
The quaternion inversion
is another fundamental, but it introduces questions f(0) = ? and "Solve f(q) = 0." Using affine transformation
s
along with the reciprocation function, one obtains the function theory of inversive quaternion geometry
.
Quaternion variable theory differs in some respects from complex variable theory as in this instance: The complex conjugate
mapping of the complex plane is a powerful tool but requires the introduction of a non-arithmetic operation. Indeed, conjugation changes the orientation
of plane figures, something that arithmetic functions do not change. In contrast, the quaternion conjugation can be expressed arithmetically:
Proposition: The function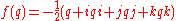
is equivalent to quaternion conjugation.
Proof: f(1) = − (1/2)(1 − 1 − 1 − 1) = 1. f(i) = −(1/2)(i − i + i + i) = − i . f(j) = − j , and f(k) = −k.
Consequently, since f is a linear function
,
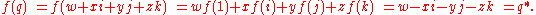
The great success of complex analysis
in providing a rich family of holomorphic function
s for scientific work has engaged some workers in efforts to extend the planar theory, based on complex numbers, to a 4-space study with functions of a quaternion variable. These efforts were summarized in 1973 by C.A. Deavours. He recalls a 1935 issue of Commentarii Mathematici Helvetici
where an alternative theory of "regular functions" was initiated by R. Feuter through the idea of Morera's theorem
: quaternion function F is "left regular at q " when the integral of F vanishes over any sufficiently small hypersurface
containing q. Then the analogue of Liouville's theorem
holds: the only quaternion function regular with bounded norm in E4 is a constant. To construct regular functions a cautious approach is to use power series with real coefficients. Deavours also gives analogues for the Poisson integral, the Cauchy integral formula, and the presentation of Maxwell’s equations of electromagnetism with quaternion functions.
Though H appears as a union of complex planes, the following proposition shows that extending complex functions requires special care:
Proposition: Let
be a function of a complex variable, 
. Suppose also that u is an even function of y and that v is an odd function of y. Then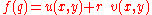 
is an extension of f to a quaternion variable 
.
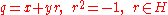proof: Let r* be the conjugate of r so that q = x − y r*. The extension to H will be complete when it is shown that f(q) = f(x − y r*). Indeed, by hypothesis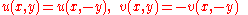
so that one obtains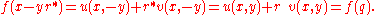
Since Hamilton it has been realized that the independence of the derivative from the path that a differential follows toward zero is an onerous restriction, excluding even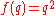
from differentiability. Therefore a direction-dependent derivative is appropriate for functions of a quaternion variable:
of a quaternionic function f(x) is given by
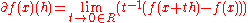
where h is a quaternion indicating the direction in which the derivative is to be taken. On the quaternions, the Gateaux derivative will always be linear in h, so it may be expressed
as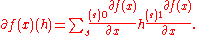
The number of terms in the sum will depend on the function f. The expressions
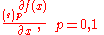
are called components of the Gateaux derivative.
For the function f(x) = axb, the derivative is
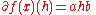
and so the components are:
|-
|
|
>
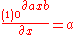
Similarly, for the function f(x) = x2, the derivative is
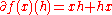
and the components are:
|-
|
|
|-
|
|
>
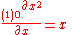
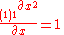
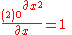
Finally, for the function f(x) = x−1, the derivative is
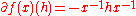
and the components are:
|-
|
|
>
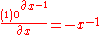
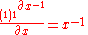Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a function of a quaternion variable is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
with domain and range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
in the quaternions H.
The projections
Projection (linear algebra)
In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself such that P2 = P. It leaves its image unchanged....
of a quaternion onto its scalar part or onto its vector part, as well as the modulus and versor functions, are examples that are basic to understanding quaternion structure. A very useful function of a quaternion variable is
which rotates the vector part of q
Quaternions and spatial rotation
Unit quaternions provide a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. Compared to Euler angles they are simpler to compose and avoid the problem of gimbal lock. Compared to rotation matrices they are more numerically stable and may...
by twice the angle of u.
The quaternion inversion
is another fundamental, but it introduces questions f(0) = ? and "Solve f(q) = 0." Using affine transformationAffine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
s
along with the reciprocation function, one obtains the function theory of inversive quaternion geometry
Inversive ring geometry
In mathematics, inversive ring geometry is the extension of the concepts of projective line, homogeneous coordinates, projective transformations, and cross-ratio to the context of associative rings, concepts usually built upon rings that happen to be fields....
.
Quaternion variable theory differs in some respects from complex variable theory as in this instance: The complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
mapping of the complex plane is a powerful tool but requires the introduction of a non-arithmetic operation. Indeed, conjugation changes the orientation
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
of plane figures, something that arithmetic functions do not change. In contrast, the quaternion conjugation can be expressed arithmetically:
Proposition: The function
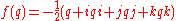is equivalent to quaternion conjugation.Proof: f(1) = − (1/2)(1 − 1 − 1 − 1) = 1. f(i) = −(1/2)(i − i + i + i) = − i . f(j) = − j , and f(k) = −k.
Consequently, since f is a linear function
Linear function
In mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....
,
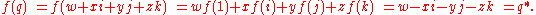
The great success of complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
in providing a rich family of holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s for scientific work has engaged some workers in efforts to extend the planar theory, based on complex numbers, to a 4-space study with functions of a quaternion variable. These efforts were summarized in 1973 by C.A. Deavours. He recalls a 1935 issue of Commentarii Mathematici Helvetici
Commentarii Mathematici Helvetici
The Commentarii Mathematici Helvetici is a scholarly journal in mathematics published by the European Mathematical Society. The Swiss Mathematical Society started the journal in 1929 after a meeting in May of the previous year. The scope of the journal includes research articles in all aspects in...
where an alternative theory of "regular functions" was initiated by R. Feuter through the idea of Morera's theorem
Morera's theorem
In complex analysis, a branch of mathematics, Morera's theorem, named after Giacinto Morera, gives an important criterion for proving that a function is holomorphic....
: quaternion function F is "left regular at q " when the integral of F vanishes over any sufficiently small hypersurface
Hypersurface
In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
containing q. Then the analogue of Liouville's theorem
Liouville's theorem (complex analysis)
In complex analysis, Liouville's theorem, named after Joseph Liouville, states that every bounded entire function must be constant. That is, every holomorphic function f for which there exists a positive number M such that |f| ≤ M for all z in C is constant.The theorem is considerably improved by...
holds: the only quaternion function regular with bounded norm in E4 is a constant. To construct regular functions a cautious approach is to use power series with real coefficients. Deavours also gives analogues for the Poisson integral, the Cauchy integral formula, and the presentation of Maxwell’s equations of electromagnetism with quaternion functions.
Though H appears as a union of complex planes, the following proposition shows that extending complex functions requires special care:
Proposition: Let
be a function of a complex variable, . Suppose also that u is an even function of y and that v is an odd function of y. Then 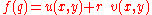is an extension of f to a quaternion variable 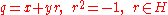.proof: Let r* be the conjugate of r so that q = x − y r*. The extension to H will be complete when it is shown that f(q) = f(x − y r*). Indeed, by hypothesis
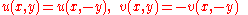so that one obtains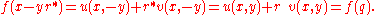Since Hamilton it has been realized that the independence of the derivative from the path that a differential follows toward zero is an onerous restriction, excluding even
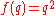from differentiability. Therefore a direction-dependent derivative is appropriate for functions of a quaternion variable:The Gâteaux derivative for quaternions
The Gâteaux derivativeGâteaux derivative
In mathematics, the Gâteaux differential or Gâteaux derivative is a generalization of the concept of directional derivative in differential calculus. Named after René Gâteaux, a French mathematician who died young in World War I, it is defined for functions between locally convex topological vector...
of a quaternionic function f(x) is given by
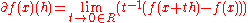
where h is a quaternion indicating the direction in which the derivative is to be taken. On the quaternions, the Gateaux derivative will always be linear in h, so it may be expressed
as
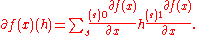
The number of terms in the sum will depend on the function f. The expressions
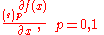
are called components of the Gateaux derivative.
For the function f(x) = axb, the derivative is
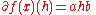
and so the components are:
|
|
>
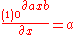
Similarly, for the function f(x) = x2, the derivative is
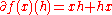
and the components are:
|
|
|-
|
|
>
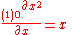
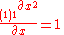
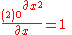
Finally, for the function f(x) = x−1, the derivative is
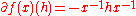
and the components are:
|
|
>
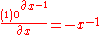
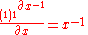