
Spin (physics)
Encyclopedia
In quantum mechanics
and particle physics
, spin is a fundamental characteristic property of elementary particle
s, composite particles (hadron
s), and atomic nuclei
.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways, but is very different from the everyday concept of spin (for example, as used when describing a spinning ball). Spin, as used by particle physicists in the quantum world, is a property of subatomic particles, which has certain qualities and obeys certain rules.
All elementary particles of a given kind have the same spin quantum number
, an important part of the quantum state of a particle. When combined with the spin-statistics theorem
, the spin of electrons results in the Pauli exclusion principle
, which in turn underlies the periodic table
of chemical element
s. The spin direction (also called spin for short) of a particle is an important intrinsic degree of freedom
.
Wolfgang Pauli
was the first to propose the concept of spin, but he did not name it. In 1925, Ralph Kronig
, George Uhlenbeck, and Samuel Goudsmit suggested a physical interpretation of particles spinning around their own axis. The mathematical theory was worked out in depth by Pauli in 1927. When Paul Dirac
derived his relativistic quantum mechanics in 1928, electron spin was an essential part of it.
Spin is a type of angular momentum
, where angular momentum is defined in the modern way as the "generator of rotations" (see Noether's theorem
). This modern definition of angular momentum is not the same as the historical classical mechanics
definition, L = r × p. (The historical definition, which does not include spin, is more specifically called "orbital angular momentum
".)
Since spin is a type of angular momentum, it has the same dimensions
: J
·s
in SI units. In practice, however, SI units are almost never used to describe spin: instead, it is written as a multiple of the reduced Planck constant ħ. In natural units
, the ħ is omitted, so the units of spin are implied. However, by definition the "spin quantum number" is always dimensionless.
angular momenta
do. On the other hand, spins have some peculiar properties that distinguish them from orbital angular momenta:
(see classical electron radius
); as far as can be determined, these elementary particles have no inner structure. The spin of an elementary particle is a truly intrinsic physical property, akin to the particle's electric charge
and rest mass.
It turns out that a convenient definition of the spin quantum number s is s = n/2, where n can be any non-negative integer
. Hence the allowed values of s are 0, 1/2, 1, 3/2, 2, etc. The value of s for an elementary particle
depends only on the type of particle, and cannot be altered in any known way (in contrast to the spin direction described below). The spin angular momentum S of any physical system is quantised
. The allowed values of S are:
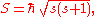
where ħ is the reduced Planck's constant. In contrast, orbital angular momentum can only take on integer quantum numbers.
All known matter
is ultimately composed of elementary particles called fermion
s, and all elementary fermions have s = 1/2. Examples of fermions are the electron
and positron
, the quark
s making up proton
s and neutron
s, and the neutrino
s. Elementary particles emit and receive one or more particles called boson
s. This boson exchange gives rise to the three fundamental interaction
s ("forces") of the Standard model of particle physics; hence bosons are also called force carriers. These bosons have s=1. A basic example for a boson is the photon
. Electromagnetism
is the force that results when charged particles exchange photons.
Theory predicts the existence of two bosons whose s differs from 1. The force carrier for gravity is the hypothetical graviton
; theory suggests that it has s = 2. The Higgs mechanism
predicts that elementary particles acquire nonzero rest mass by exchanging hypothetical Higgs boson
s with an all-pervasive Higgs field. Theory predicts that the Higgs boson has s = 0. If so, it would be the only elementary particle for which this is the case.
s, neutron
s, and atomic nuclei
is usually understood to mean the total angular momentum. This is the sum of the spins and orbital angular momenta of the constituent particles. Such a composite spin is subject to the same quantization condition as any other angular momentum.
Composite particles are often referred to as having a definite spin, just like elementary particles; for example, the proton is a spin-1/2 particle. This is understood to refer to the spin of the lowest-energy internal state of the composite particle (i.e., a given spin and orbital configuration of the constituents).
It is not always easy to deduce the spin of a composite particle from first principles. For example, even though we know that the proton is a spin-1/2 particle, the question of how this spin is distributed
among the three internal valence quarks and the surrounding sea quarks and gluon
s is an active area of research.
Delta baryon
s, which decay into protons and neutrons, have spin 3/2. All the three quarks inside a Delta baryon
(Δ) have their spin axis pointing in the same direction, unlike the nearly identical proton and neutron (called "nucleons") in which the intrinsic spin of one of the three constituent quarks is always opposite the spin of the other two. This difference in spin alignment is the only quantum number distinction between the Δ+ and Δ0 and ordinary nucleons.
.
. Particles with half-integer spin obey Fermi-Dirac statistics
, and are known as fermion
s. They are required to occupy antisymmetric quantum states (see the article on identical particles
.) This property forbids fermions from sharing quantum states – a restriction known as the Pauli exclusion principle
. Particles with integer spin, on the other hand, obey Bose-Einstein statistics, and are known as boson
s. These particles occupy "symmetric states", and can therefore share quantum states. The proof of this is known as the spin-statistics theorem
, which relies on both quantum mechanics and the theory of special relativity
. In fact, "the connection between spin and statistics is one of the most important applications of the special relativity theory".
 Particles with spin can possess a magnetic dipole moment, just like a rotating electrically charged
Particles with spin can possess a magnetic dipole moment, just like a rotating electrically charged
body in classical electrodynamics. These magnetic moments can be experimentally observed in several ways, e.g. by the deflection of particles by inhomogeneous magnetic field
s in a Stern–Gerlach experiment
, or by measuring the magnetic fields generated by the particles themselves.
The intrinsic magnetic moment μ of an elementary particle with charge q, mass m, and spin angular momentum S, is
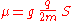
where the dimensionless quantity
g is called the g-factor. For exclusively orbital rotations it would be 1 (assuming that the mass and the charge occupy spheres of equal radius).
The electron, being a charged elementary particle, possesses a nonzero magnetic moment
. One of the triumphs of the theory of quantum electrodynamics
is its accurate prediction of the electron g-factor
, which has been experimentally determined to have the value , with the digits in parentheses denoting measurement uncertainty
in the last two digits at one standard deviation
. The value of 2 arises from the Dirac equation
, a fundamental equation connecting the electron's spin with its electromagnetic properties, and the correction of ... arises from the electron's interaction with the surrounding electromagnetic field
, including its own field. Composite particles also possess magnetic moments associated with their spin. In particular, the neutron possesses a non-zero magnetic moment despite being electrically neutral. This fact was an early indication that the neutron is not an elementary particle. In fact, it is made up of quarks, which are electrically charged particles. The magnetic moment of the neutron comes from the spins of the individual quarks and their orbital motions.
Neutrino
s are both elementary and electrically neutral. The minimally extended Standard Model
that takes into account non-zero neutrino masses predicts neutrino magnetic moments of:
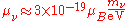
where the μν are the neutrino magnetic moments, mν are the neutrino masses, and μB is the Bohr magneton. New physics above the electroweak scale could, however, lead to significantly higher neutrino magnetic moments. It can be shown in a model independent way that neutrino magnetic moments larger than about 10−14 μB are unnatural, because they would also lead to large radiative contributions to the neutrino mass. Since the neutrino masses cannot exceed about 1 eV, these radiative corrections must then be assumed to be fine tuned to cancel out to a large degree.
The measurement of neutrino magnetic moments is an active area of research. , the latest experimental results have put the neutrino magnetic moment at less than times the electron's magnetic moment.
In ordinary material
s, the magnetic dipole moments of individual atoms produce magnetic fields that cancel one another, because each dipole points in a random direction. Ferromagnetic materials below their Curie temperature, however, exhibit magnetic domains in which the atomic dipole moments are locally aligned, producing a macroscopic, non-zero magnetic field from the domain. These are the ordinary "magnets" with which we are all familiar.
In paramagnetic materials, the magnetic dipole moments of individual atoms spontaneously align with an externally applied magnetic field. In diamagnetic materials, on the other hand, the magnetic dipole moments of individual atoms spontaneously align oppositely to any externally applied magnetic field, even if it requires energy to do so.
The study of the behavior of such "spin model
s" is a thriving area of research in condensed matter physics
. For instance, the Ising model
describes spins (dipoles) that have only two possible states, up and down, whereas in the Heisenberg model
the spin vector is allowed to point in any direction. These models have many interesting properties, which have led to interesting results in the theory of phase transition
s.

where s is the principal spin quantum number discussed in the previous section. One can see that there are 2s+1 possible values of sz. The number "2s + 1" is the multiplicity of the spin system. For example, there are only two possible values for a spin-1/2 particle: sz = +1/2 and sz = −1/2. These correspond to quantum states in which the spin is pointing in the +z or −z directions respectively, and are often referred to as "spin up" and "spin down". For a spin-3/2 particle, like a delta baryon
, the possible values are +3/2, +1/2, −1/2, −3/2.
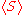 whose components are the expectation values of the spin components along each axis, i.e.,
whose components are the expectation values of the spin components along each axis, i.e.,  . This vector then would describe the "direction" in which the spin is pointing, corresponding to the classical concept of the axis of rotation. It turns out that the spin vector is not very useful in actual quantum mechanical calculations, because it cannot be measured directly — sx, sy and sz cannot possess simultaneous definite values, because of a quantum uncertainty relation
. This vector then would describe the "direction" in which the spin is pointing, corresponding to the classical concept of the axis of rotation. It turns out that the spin vector is not very useful in actual quantum mechanical calculations, because it cannot be measured directly — sx, sy and sz cannot possess simultaneous definite values, because of a quantum uncertainty relation
between them. However, for statistically large collections of particles that have been placed in the same pure quantum state, such as through the use of a Stern-Gerlach apparatus, the spin vector does have a well-defined experimental meaning: It specifies the direction in ordinary space in which a subsequent detector must be oriented in order to achieve the maximum possible probability (100%) of detecting every particle in the collection. For spin-1/2 particles, this maximum probability drops off smoothly as the angle between the spin vector and the detector increases, until at an angle of 180 degrees—that is, for detectors oriented in the opposite direction to the spin vector—the expectation of detecting particles from the collection reaches a minimum of 0%.
As a qualitative concept, the spin vector is often handy because it is easy to picture classically. For instance, quantum mechanical spin can exhibit phenomena analogous to classical gyroscopic effects
. For example, one can exert a kind of "torque
" on an electron by putting it in a magnetic field
(the field acts upon the electron's intrinsic magnetic dipole moment—see the following section). The result is that the spin vector undergoes precession
, just like a classical gyroscope. This phenomenon is used in nuclear magnetic resonance
sensing.
Mathematically, quantum mechanical spin is not described by vectors as in classical angular momentum, but by objects known as spinor
s. There are subtle differences between the behavior of spinors and vectors under coordinate rotations. For example, rotating a spin-1/2 particle by 360 degrees does not bring it back to the same quantum state, but to the state with the opposite quantum phase
; this is detectable, in principle, with interference experiments. To return the particle to its exact original state, one needs a 720 degree rotation. A spin-zero particle can only have a single quantum state, even after torque is applied. Rotating a spin-2 particle 180 degrees can bring it back to the same quantum state and a spin-4 particle should be rotated 90 degrees to bring it back to the same quantum state. The spin 2 particle can be analogous to a straight stick that looks the same even after it is rotated 180 degrees and a spin 0 particle can be imagined as sphere which looks the same after whatever angle it is turned through.
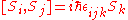
where is the Levi-Civita symbol
is the Levi-Civita symbol
. It follows (as with angular momentum
) that the eigenvectors of S2 and Sz (expressed as ket
s in the total S basis
) are:


The spin raising and lowering operators
acting on these eigenvectors give:
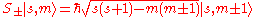 , where
, where 
But unlike orbital angular momentum the eigenvectors are not spherical harmonics
. They are not functions of θ and φ. There is also no reason to exclude half-integer values of s and m.
In addition to their other properties, all quantum mechanical particles possess an intrinsic spin (though it may have the intrinsic spin 0, too). The spin is quantized in units of the reduced Planck constant, such that the state function of the particle is, e.g., not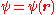 , but
, but 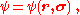 where
where  is out of the following discrete set of values:
is out of the following discrete set of values:
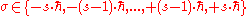 .
.
One distinguishes boson
s (integer spin) and fermion
s (half-integer spin). The total angular momentum conserved in interaction processes is then the sum of the orbital angular momentum and the spin.
operators associated with spin observables are:
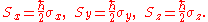
In the special case of spin-1/2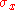 ,
, 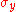 and
and 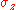 are the three Pauli matrices
are the three Pauli matrices
, given by:
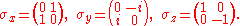
, which states that by interchanges of any two of the N particles one must have
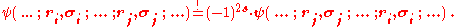
Thus, for bosons the prefactor (−1)2s will reduce to +1, for fermions to −1. In quantum mechanics all particles are either bosons or fermions. In relativistic quantum field theories also "supersymmetric
" particles exist, where linear combinations of bosonic and fermionic components appear. In two dimensions, the prefactor (−1)2s can be replaced by any complex number of magnitude 1 (see Anyon
).
Electrons are fermions with s = 1/2; quanta of light ("photon
s") are bosons with s = 1. This shows also explicitly that the property spin cannot be fully explained as a classical intrinsic orbital angular momentum, e.g., similar to that of a "spinning top", since orbital angular rotations would lead to integer values of s. Instead one is dealing with an essential legacy of relativity. The photon, in contrast, is always relativistic (velocity v ≈ c
), and the corresponding classical theory, that of Maxwell, is also relativistic.
The above permutation postulate for N-particle state functions has most-important consequences in daily life, e.g. the periodic table
of the chemists or biologists.
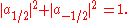
For a generic particle with spin s, we would need 2s+1 such parameters. Since these numbers depend on the choice of the axis, they transform into each other non-trivially when this axis is rotated. It's clear that the transformation law must be linear, so we can represent it by associating a matrix with each rotation, and the product of two transformation matrices corresponding to rotations A and B must be equal (up to phase) to the matrix representing rotation AB. Further, rotations preserve the quantum mechanical inner product, and so should our transformation matrices:
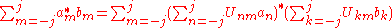
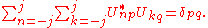
Mathematically speaking, these matrices furnish a unitary projective
representation
of the rotation group
SO(3). Each such representation corresponds to a representation of the covering group of SO(3), which is SU(2). There is one n-dimensional irreducible representation of SU(2) for each dimension, though this representation is n-dimensional real for odd n and n-dimensional complex for even n (hence of real dimension 2n). For a rotation by angle θ in the plane with normal vector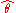 , U can be written
, U can be written
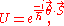
where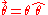 and
and 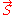 is the vector of spin operators.
is the vector of spin operators.
A generic rotation in 3-dimensional space can be built by compounding operators of this type using Euler angles
: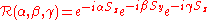
An irreducible representation of this group of operators is furnished by the Wigner D-matrix
: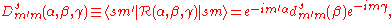
where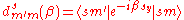
is Wigner's small d-matrix. Note that for γ = 2π and α = β = 0, i.e. a full rotation about the z-axis, the Wigner D-matrix elements become
Recalling that a generic spin state can be written as a superposition of states with definite m, we see that if s is an integer, the values of m are all integers, and this matrix corresponds to the identity operator. However, if s is a half-integer, the values of m are also all half-integers, giving (-1)2m = -1 for all m, and hence upon rotation by 2π the state picks up a minus sign. This fact is a crucial element of the proof of the spin-statistics theorem
.
s, but we'd immediately discover a major obstacle. Unlike SO(3), the group of Lorentz transformations SO(3,1) is non-compact
and therefore does not have any faithful unitary finite-dimensional representations.
In case of spin 1/2 particles, it is possible to find a construction that includes both a finite-dimensional representation and a scalar product that is preserved by this representation. We associate a 4-component Dirac spinor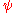 with each particle. These spinors transform under Lorentz transformations according to the law
with each particle. These spinors transform under Lorentz transformations according to the law

where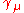 are gamma matrices and
are gamma matrices and  is an antisymmetric 4x4 matrix parametrizing the transformation. It can be shown that the scalar product
is an antisymmetric 4x4 matrix parametrizing the transformation. It can be shown that the scalar product
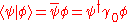
is preserved. (It is not, however, positive definite, so the representation is not unitary.)

By the postulates of quantum mechanics, an experiment designed to measure the electron spin on the x, y or z axis can only yield an eigenvalue of the corresponding spin operator ( or
or  ) on that axis, i.e.
) on that axis, i.e.  or
or 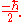 The quantum state of a particle (with respect to spin), can be represented by a two component spinor
The quantum state of a particle (with respect to spin), can be represented by a two component spinor
:
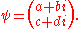
When the spin of this particle is measured with respect to a given axis (in this example, the x-axis), the probability that its spin will be measured as is just
is just  . Correspondingly, the probability that its spin will be measured as
. Correspondingly, the probability that its spin will be measured as 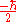 is just
is just  . Following the measurement, the spin state of the particle will collapse
. Following the measurement, the spin state of the particle will collapse
into the corresponding eigenstate. As a result, if the particle's spin along a given axis has been measured to have a given eigenvalue, all measurements will yield the same eigenvalue (since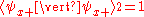 , etc), provided that no measurements of the spin are made along other axes (see compatibility section below).
, etc), provided that no measurements of the spin are made along other axes (see compatibility section below).
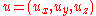 be an arbitrary unit vector. Then the operator for spin in this direction is simply
be an arbitrary unit vector. Then the operator for spin in this direction is simply 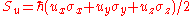 . The operator
. The operator 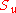 has eigenvalues of
has eigenvalues of 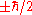 , just like the usual spin matrices. This method of finding the operator for spin in an arbitrary direction generalizes to higher spin states, one takes the dot product of the direction with a vector of the three operators for the three x,y,z axis directions.
, just like the usual spin matrices. This method of finding the operator for spin in an arbitrary direction generalizes to higher spin states, one takes the dot product of the direction with a vector of the three operators for the three x,y,z axis directions.
A normalized spinor for spin-1/2 in the direction (which works for all spin states except spin down where it will give 0/0), is:
direction (which works for all spin states except spin down where it will give 0/0), is:
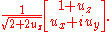
The above spinor is obtained in the usual way by diagonalizing the matrix and finding the eigenstates corresponding to the eigenvalues.
matrix and finding the eigenstates corresponding to the eigenvalues.
In quantum mechanics, vectors are termed "normalized" when multiplied by a normalizing factor, which results in the vector having a length of unity.
, measurements of spin along the different axes are incompatible. This means that if, for example, we know the spin along the x-axis, and we then measure the spin along the y-axis, we have invalidated our previous knowledge of the x-axis spin. This can be seen from the property of the eigenvectors (i.e. eigenstates) of the Pauli matrices that:

So when we measure the spin of a particle along the x-axis as, for example, , the particle's spin state collapses
, the particle's spin state collapses
into the eigenstate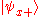 . When we then subsequently measure the particle's spin along the y-axis, the spin state will now collapse into either
. When we then subsequently measure the particle's spin along the y-axis, the spin state will now collapse into either 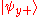 or
or 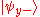 , each with probability
, each with probability  . Let us say, in our example, that we measure
. Let us say, in our example, that we measure 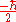 . When we now return to measure the particle's spin along the x-axis again, the probabilities that we will measure
. When we now return to measure the particle's spin along the x-axis again, the probabilities that we will measure  or
or  are each
are each  (i.e. they are
(i.e. they are 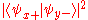 and
and  ). This implies that our original measurement of the spin along the x-axis is no longer valid, since the spin along the x-axis will now be measured to have either eigenvalue with equal probability.
). This implies that our original measurement of the spin along the x-axis is no longer valid, since the spin along the x-axis will now be measured to have either eigenvalue with equal probability.
with "+" for even parity (wave function unchanged by spatial inversion) and "-" for odd parity (wave function negated by spatial inversion). For example, see the isotopes of bismuth
.
Electron spin plays an important role in magnetism
, with applications for instance in computer memories. The manipulation of nuclear spin by radiofrequency waves (nuclear magnetic resonance
) is important in chemical spectroscopy and medical imaging.
Spin-orbit coupling leads to the fine structure
of atomic spectra, which is used in atomic clock
s and in the modern definition of the second
. Precise measurements of the g-factor of the electron have played an important role in the development and verification of quantum electrodynamics
. Photon spin is associated with the polarization of light.
A possible future direct application of spin is as a binary information carrier in spin transistor
s. Original concept proposed in 1990 is known as Datta-Das spin transistor. Electronics based on spin transistors is called spintronics
, which includes the manipulation of spins in semiconductor devices.
There are many indirect applications and manifestations of spin and the associated Pauli exclusion principle
, starting with the periodic table
of chemistry.
of alkali metal
s. In 1924 Wolfgang Pauli introduced what he called a "two-valued quantum degree of freedom" associated with the electron in the outermost shell
. This allowed him to formulate the Pauli exclusion principle
, stating that no two electrons can share the same quantum state at the same time.
The physical interpretation of Pauli's "degree of freedom" was initially unknown. Ralph Kronig
, one of Landé
's assistants, suggested in early 1925 that it was produced by the self-rotation of the electron. When Pauli heard about the idea, he criticized it severely, noting that the electron's hypothetical surface would have to be moving faster than the speed of light
in order for it to rotate quickly enough to produce the necessary angular momentum. This would violate the theory of relativity
. Largely due to Pauli's criticism, Kronig decided not to publish his idea.
In the autumn of 1925, the same thought came to two Dutch physicists, George Uhlenbeck and Samuel Goudsmit. Under the advice of Paul Ehrenfest
, they published their results. It met a favorable response, especially after Llewellyn Thomas
managed to resolve a factor-of-two discrepancy between experimental results and Uhlenbeck and Goudsmit's calculations (and Kronig's unpublished ones). This discrepancy was due to the orientation of the electron's tangent frame, in addition to its position.
Mathematically speaking, a fiber bundle
description is needed. The tangent bundle
effect is additive and relativistic; that is, it vanishes if c goes to infinity. It is one half of the value obtained without regard for the tangent space orientation, but with opposite sign. Thus the combined effect differs from the latter by a factor two (Thomas precession
).
Despite his initial objections, Pauli formalized the theory of spin in 1927, using the modern theory of quantum mechanics
discovered by Schrödinger
and Heisenberg
. He pioneered the use of Pauli matrices
as a representation
of the spin operators, and introduced a two-component spinor
wave-function.
Pauli's theory of spin was non-relativistic. However, in 1928, Paul Dirac
published the Dirac equation
, which described the relativistic electron
. In the Dirac equation, a four-component spinor (known as a "Dirac spinor") was used for the electron wave-function. In 1940, Pauli proved the spin-statistics theorem
, which states that fermion
s have half-integer spin and boson
s integer spin.
In retrospect, the first direct experimental evidence of the electron spin was the Stern-Gerlach experiment of 1922. However, the correct explanation of this experiment was only given in 1927.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
and particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
, spin is a fundamental characteristic property of elementary particle
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
s, composite particles (hadron
Hadron
In particle physics, a hadron is a composite particle made of quarks held together by the strong force...
s), and atomic nuclei
Atomic nucleus
The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways, but is very different from the everyday concept of spin (for example, as used when describing a spinning ball). Spin, as used by particle physicists in the quantum world, is a property of subatomic particles, which has certain qualities and obeys certain rules.
All elementary particles of a given kind have the same spin quantum number
Quantum number
Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...
, an important part of the quantum state of a particle. When combined with the spin-statistics theorem
Spin-statistics theorem
In quantum mechanics, the spin-statistics theorem relates the spin of a particle to the particle statistics it obeys. The spin of a particle is its intrinsic angular momentum...
, the spin of electrons results in the Pauli exclusion principle
Pauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
, which in turn underlies the periodic table
Periodic table
The periodic table of the chemical elements is a tabular display of the 118 known chemical elements organized by selected properties of their atomic structures. Elements are presented by increasing atomic number, the number of protons in an atom's atomic nucleus...
of chemical element
Chemical element
A chemical element is a pure chemical substance consisting of one type of atom distinguished by its atomic number, which is the number of protons in its nucleus. Familiar examples of elements include carbon, oxygen, aluminum, iron, copper, gold, mercury, and lead.As of November 2011, 118 elements...
s. The spin direction (also called spin for short) of a particle is an important intrinsic degree of freedom
Degrees of freedom (physics and chemistry)
A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
.
Wolfgang Pauli
Wolfgang Pauli
Wolfgang Ernst Pauli was an Austrian theoretical physicist and one of the pioneers of quantum physics. In 1945, after being nominated by Albert Einstein, he received the Nobel Prize in Physics for his "decisive contribution through his discovery of a new law of Nature, the exclusion principle or...
was the first to propose the concept of spin, but he did not name it. In 1925, Ralph Kronig
Ralph Kronig
Ralph Kronig was a German-American physicist . He is noted for the discovery of particle spin and for his theory of x-ray absorption spectroscopy...
, George Uhlenbeck, and Samuel Goudsmit suggested a physical interpretation of particles spinning around their own axis. The mathematical theory was worked out in depth by Pauli in 1927. When Paul Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
derived his relativistic quantum mechanics in 1928, electron spin was an essential part of it.
Spin is a type of angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
, where angular momentum is defined in the modern way as the "generator of rotations" (see Noether's theorem
Noether's theorem
Noether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
). This modern definition of angular momentum is not the same as the historical classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
definition, L = r × p. (The historical definition, which does not include spin, is more specifically called "orbital angular momentum
Angular momentum operator
In quantum mechanics, the angular momentum operator is an operator analogous to classical angular momentum. The angular momentum operator plays a central role in the theory of atomic physics and other quantum problems involving rotational symmetry...
".)
Since spin is a type of angular momentum, it has the same dimensions
Dimensions
Dimensions is a French project that makes educational movies about mathematics, focusing on spatial geometry. It uses POV-Ray to render some of the animations, and the films are release under a Creative Commons licence....
: J
Joule
The joule ; symbol J) is a derived unit of energy or work in the International System of Units. It is equal to the energy expended in applying a force of one newton through a distance of one metre , or in passing an electric current of one ampere through a resistance of one ohm for one second...
·s
Second
The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
in SI units. In practice, however, SI units are almost never used to describe spin: instead, it is written as a multiple of the reduced Planck constant ħ. In natural units
Natural units
In physics, natural units are physical units of measurement based only on universal physical constants. For example the elementary charge e is a natural unit of electric charge, or the speed of light c is a natural unit of speed...
, the ħ is omitted, so the units of spin are implied. However, by definition the "spin quantum number" is always dimensionless.
Spin quantum number
As the name suggests, spin was originally conceived as the rotation of a particle around some axis. This picture is correct so far as spins obey the same mathematical laws as quantizedQuantization (physics)
In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...
angular momenta
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
do. On the other hand, spins have some peculiar properties that distinguish them from orbital angular momenta:
- Spin quantum numbers may take on half-odd-integer values;
- Although the direction of its spin can be changed, an elementary particle cannot be made to spin faster or slower.
- The spin of a charged particle is associated with a magnetic dipole moment with a g-factor differing from 1. This could only occur classically if the internal charge of the particle were distributed differently from its mass.
Elementary particles
Elementary particles are particles for which there is no known method of division into smaller units. Theoretical and experimental studies have shown that the spin possessed by such particles cannot be explained by postulating that they are made up of even smaller particles rotating about a common center of massCenter of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
(see classical electron radius
Classical electron radius
The classical electron radius, also known as the Lorentz radius or the Thomson scattering length, is based on a classical relativistic model of the electron...
); as far as can be determined, these elementary particles have no inner structure. The spin of an elementary particle is a truly intrinsic physical property, akin to the particle's electric charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
and rest mass.
It turns out that a convenient definition of the spin quantum number s is s = n/2, where n can be any non-negative integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
. Hence the allowed values of s are 0, 1/2, 1, 3/2, 2, etc. The value of s for an elementary particle
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
depends only on the type of particle, and cannot be altered in any known way (in contrast to the spin direction described below). The spin angular momentum S of any physical system is quantised
Quantization (physics)
In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...
. The allowed values of S are:
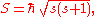
where ħ is the reduced Planck's constant. In contrast, orbital angular momentum can only take on integer quantum numbers.
All known matter
Matter
Matter is a general term for the substance of which all physical objects consist. Typically, matter includes atoms and other particles which have mass. A common way of defining matter is as anything that has mass and occupies volume...
is ultimately composed of elementary particles called fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s, and all elementary fermions have s = 1/2. Examples of fermions are the electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
and positron
Positron
The positron or antielectron is the antiparticle or the antimatter counterpart of the electron. The positron has an electric charge of +1e, a spin of ½, and has the same mass as an electron...
, the quark
Quark
A quark is an elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. Due to a phenomenon known as color confinement, quarks are never directly...
s making up proton
Proton
The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
s and neutron
Neutron
The neutron is a subatomic hadron particle which has the symbol or , no net electric charge and a mass slightly larger than that of a proton. With the exception of hydrogen, nuclei of atoms consist of protons and neutrons, which are therefore collectively referred to as nucleons. The number of...
s, and the neutrino
Neutrino
A neutrino is an electrically neutral, weakly interacting elementary subatomic particle with a half-integer spin, chirality and a disputed but small non-zero mass. It is able to pass through ordinary matter almost unaffected...
s. Elementary particles emit and receive one or more particles called boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s. This boson exchange gives rise to the three fundamental interaction
Fundamental interaction
In particle physics, fundamental interactions are the ways that elementary particles interact with one another...
s ("forces") of the Standard model of particle physics; hence bosons are also called force carriers. These bosons have s=1. A basic example for a boson is the photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
. Electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
is the force that results when charged particles exchange photons.
Theory predicts the existence of two bosons whose s differs from 1. The force carrier for gravity is the hypothetical graviton
Graviton
In physics, the graviton is a hypothetical elementary particle that mediates the force of gravitation in the framework of quantum field theory. If it exists, the graviton must be massless and must have a spin of 2...
; theory suggests that it has s = 2. The Higgs mechanism
Higgs mechanism
In particle physics, the Higgs mechanism is the process in which gauge bosons in a gauge theory can acquire non-vanishing masses through absorption of Nambu-Goldstone bosons arising in spontaneous symmetry breaking....
predicts that elementary particles acquire nonzero rest mass by exchanging hypothetical Higgs boson
Higgs boson
The Higgs boson is a hypothetical massive elementary particle that is predicted to exist by the Standard Model of particle physics. Its existence is postulated as a means of resolving inconsistencies in the Standard Model...
s with an all-pervasive Higgs field. Theory predicts that the Higgs boson has s = 0. If so, it would be the only elementary particle for which this is the case.
Composite particles
The spin of composite particles, such as protonProton
The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
s, neutron
Neutron
The neutron is a subatomic hadron particle which has the symbol or , no net electric charge and a mass slightly larger than that of a proton. With the exception of hydrogen, nuclei of atoms consist of protons and neutrons, which are therefore collectively referred to as nucleons. The number of...
s, and atomic nuclei
Atomic nucleus
The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
is usually understood to mean the total angular momentum. This is the sum of the spins and orbital angular momenta of the constituent particles. Such a composite spin is subject to the same quantization condition as any other angular momentum.
Composite particles are often referred to as having a definite spin, just like elementary particles; for example, the proton is a spin-1/2 particle. This is understood to refer to the spin of the lowest-energy internal state of the composite particle (i.e., a given spin and orbital configuration of the constituents).
It is not always easy to deduce the spin of a composite particle from first principles. For example, even though we know that the proton is a spin-1/2 particle, the question of how this spin is distributed
Nucleon spin structure
Nucleon spin structure describes the partonic structure of nucleon intrinsic angular momentum . The key question is how nucleon spin 1/2 is carried by its constituents, say partons . It was originally expected before the 1980s that quarks carry all of the nucleon spin, but later experiments...
among the three internal valence quarks and the surrounding sea quarks and gluon
Gluon
Gluons are elementary particles which act as the exchange particles for the color force between quarks, analogous to the exchange of photons in the electromagnetic force between two charged particles....
s is an active area of research.
Delta baryon
Delta baryon
The Delta baryons are a family of subatomic hadron particles which have the symbols , , , and and electric charges +2, +1, 0 and -1 elementary charge respectively...
s, which decay into protons and neutrons, have spin 3/2. All the three quarks inside a Delta baryon
Delta baryon
The Delta baryons are a family of subatomic hadron particles which have the symbols , , , and and electric charges +2, +1, 0 and -1 elementary charge respectively...
(Δ) have their spin axis pointing in the same direction, unlike the nearly identical proton and neutron (called "nucleons") in which the intrinsic spin of one of the three constituent quarks is always opposite the spin of the other two. This difference in spin alignment is the only quantum number distinction between the Δ+ and Δ0 and ordinary nucleons.
Atoms and molecules
The spin of atoms and molecules is the sum of the spins of unpaired electrons, which may be parallel or antiparallel. It is responsible for paramagnetismParamagnetism
Paramagnetism is a form of magnetism whereby the paramagnetic material is only attracted when in the presence of an externally applied magnetic field. In contrast with this, diamagnetic materials are repulsive when placed in a magnetic field...
.
The spin-statistics theorem
The spin of a particle has crucial consequences for its properties in statistical mechanicsStatistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
. Particles with half-integer spin obey Fermi-Dirac statistics
Fermi-Dirac statistics
Fermi–Dirac statistics is a part of the science of physics that describes the energies of single particles in a system comprising many identical particles that obey the Pauli Exclusion Principle...
, and are known as fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s. They are required to occupy antisymmetric quantum states (see the article on identical particles
Identical particles
Identical particles, or indistinguishable particles, are particles that cannot be distinguished from one another, even in principle. Species of identical particles include elementary particles such as electrons, and, with some clauses, composite particles such as atoms and molecules.There are two...
.) This property forbids fermions from sharing quantum states – a restriction known as the Pauli exclusion principle
Pauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
. Particles with integer spin, on the other hand, obey Bose-Einstein statistics, and are known as boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s. These particles occupy "symmetric states", and can therefore share quantum states. The proof of this is known as the spin-statistics theorem
Spin-statistics theorem
In quantum mechanics, the spin-statistics theorem relates the spin of a particle to the particle statistics it obeys. The spin of a particle is its intrinsic angular momentum...
, which relies on both quantum mechanics and the theory of special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
. In fact, "the connection between spin and statistics is one of the most important applications of the special relativity theory".
Magnetic moments

Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
body in classical electrodynamics. These magnetic moments can be experimentally observed in several ways, e.g. by the deflection of particles by inhomogeneous magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
s in a Stern–Gerlach experiment
Stern–Gerlach experiment
Important in the field of quantum mechanics, the Stern–Gerlach experiment, named after Otto Stern and Walther Gerlach, is a 1922 experiment on the deflection of particles, often used to illustrate basic principles of quantum mechanics...
, or by measuring the magnetic fields generated by the particles themselves.
The intrinsic magnetic moment μ of an elementary particle with charge q, mass m, and spin angular momentum S, is
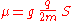
where the dimensionless quantity
Dimensionless quantity
In dimensional analysis, a dimensionless quantity or quantity of dimension one is a quantity without an associated physical dimension. It is thus a "pure" number, and as such always has a dimension of 1. Dimensionless quantities are widely used in mathematics, physics, engineering, economics, and...
g is called the g-factor. For exclusively orbital rotations it would be 1 (assuming that the mass and the charge occupy spheres of equal radius).
The electron, being a charged elementary particle, possesses a nonzero magnetic moment
Electron magnetic dipole moment
In atomic physics, the electron magnetic dipole moment is the magnetic moment of an electron caused by its intrinsic property of spin.-Magnetic moment of an electron:...
. One of the triumphs of the theory of quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
is its accurate prediction of the electron g-factor
Landé g-factor
In physics, the Landé g-factor is a particular example of a g-factor, namely for an electron with both spin and orbital angular momenta. It is named after Alfred Landé, who first described it in 1921....
, which has been experimentally determined to have the value , with the digits in parentheses denoting measurement uncertainty
Measurement uncertainty
In metrology, measurement uncertainty is a non-negative parameter characterizing the dispersion of the values attributed to a measured quantity. The uncertainty has a probabilistic basis and reflects incomplete knowledge of the quantity. All measurements are subject to uncertainty and a measured...
in the last two digits at one standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
. The value of 2 arises from the Dirac equation
Dirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
, a fundamental equation connecting the electron's spin with its electromagnetic properties, and the correction of ... arises from the electron's interaction with the surrounding electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
, including its own field. Composite particles also possess magnetic moments associated with their spin. In particular, the neutron possesses a non-zero magnetic moment despite being electrically neutral. This fact was an early indication that the neutron is not an elementary particle. In fact, it is made up of quarks, which are electrically charged particles. The magnetic moment of the neutron comes from the spins of the individual quarks and their orbital motions.
Neutrino
Neutrino
A neutrino is an electrically neutral, weakly interacting elementary subatomic particle with a half-integer spin, chirality and a disputed but small non-zero mass. It is able to pass through ordinary matter almost unaffected...
s are both elementary and electrically neutral. The minimally extended Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
that takes into account non-zero neutrino masses predicts neutrino magnetic moments of:
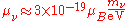
where the μν are the neutrino magnetic moments, mν are the neutrino masses, and μB is the Bohr magneton. New physics above the electroweak scale could, however, lead to significantly higher neutrino magnetic moments. It can be shown in a model independent way that neutrino magnetic moments larger than about 10−14 μB are unnatural, because they would also lead to large radiative contributions to the neutrino mass. Since the neutrino masses cannot exceed about 1 eV, these radiative corrections must then be assumed to be fine tuned to cancel out to a large degree.
The measurement of neutrino magnetic moments is an active area of research. , the latest experimental results have put the neutrino magnetic moment at less than times the electron's magnetic moment.
In ordinary material
Material
Material is anything made of matter, constituted of one or more substances. Wood, cement, hydrogen, air and water are all examples of materials. Sometimes the term "material" is used more narrowly to refer to substances or components with certain physical properties that are used as inputs to...
s, the magnetic dipole moments of individual atoms produce magnetic fields that cancel one another, because each dipole points in a random direction. Ferromagnetic materials below their Curie temperature, however, exhibit magnetic domains in which the atomic dipole moments are locally aligned, producing a macroscopic, non-zero magnetic field from the domain. These are the ordinary "magnets" with which we are all familiar.
In paramagnetic materials, the magnetic dipole moments of individual atoms spontaneously align with an externally applied magnetic field. In diamagnetic materials, on the other hand, the magnetic dipole moments of individual atoms spontaneously align oppositely to any externally applied magnetic field, even if it requires energy to do so.
The study of the behavior of such "spin model
Spin model
A spin model is a mathematical model used in physics primarily to explain magnetism. Spin models may either be classical or quantum mechanical in nature. Spin models have been studied in quantum field theory as examples of integrable models. Spin models are also used in quantum information theory...
s" is a thriving area of research in condensed matter physics
Condensed matter physics
Condensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
. For instance, the Ising model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
describes spins (dipoles) that have only two possible states, up and down, whereas in the Heisenberg model
Heisenberg model
The Heisenberg model can refer to two models in statistical mechanics:*Heisenberg model , a classical nearest neighbour spin model*Heisenberg model , a model where the spins are treated quantum mechanically using Pauli matrices....
the spin vector is allowed to point in any direction. These models have many interesting properties, which have led to interesting results in the theory of phase transition
Phase transition
A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....
s.
Spin projection quantum number and spin multiplicity
In classical mechanics, the angular momentum of a particle possesses not only a magnitude (how fast the body is rotating), but also a direction (either up or down on the axis of rotation of the particle). Quantum mechanical spin also contains information about direction, but in a more subtle form. Quantum mechanics states that the component of angular momentum measured along any direction (say along the z-axis) can only take on the values
where s is the principal spin quantum number discussed in the previous section. One can see that there are 2s+1 possible values of sz. The number "2s + 1" is the multiplicity of the spin system. For example, there are only two possible values for a spin-1/2 particle: sz = +1/2 and sz = −1/2. These correspond to quantum states in which the spin is pointing in the +z or −z directions respectively, and are often referred to as "spin up" and "spin down". For a spin-3/2 particle, like a delta baryon
Delta baryon
The Delta baryons are a family of subatomic hadron particles which have the symbols , , , and and electric charges +2, +1, 0 and -1 elementary charge respectively...
, the possible values are +3/2, +1/2, −1/2, −3/2.
Spin vector
For a given quantum state, one could think of a spin vector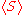 whose components are the expectation values of the spin components along each axis, i.e.,
whose components are the expectation values of the spin components along each axis, i.e.,  . This vector then would describe the "direction" in which the spin is pointing, corresponding to the classical concept of the axis of rotation. It turns out that the spin vector is not very useful in actual quantum mechanical calculations, because it cannot be measured directly — sx, sy and sz cannot possess simultaneous definite values, because of a quantum uncertainty relation
. This vector then would describe the "direction" in which the spin is pointing, corresponding to the classical concept of the axis of rotation. It turns out that the spin vector is not very useful in actual quantum mechanical calculations, because it cannot be measured directly — sx, sy and sz cannot possess simultaneous definite values, because of a quantum uncertainty relationUncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
between them. However, for statistically large collections of particles that have been placed in the same pure quantum state, such as through the use of a Stern-Gerlach apparatus, the spin vector does have a well-defined experimental meaning: It specifies the direction in ordinary space in which a subsequent detector must be oriented in order to achieve the maximum possible probability (100%) of detecting every particle in the collection. For spin-1/2 particles, this maximum probability drops off smoothly as the angle between the spin vector and the detector increases, until at an angle of 180 degrees—that is, for detectors oriented in the opposite direction to the spin vector—the expectation of detecting particles from the collection reaches a minimum of 0%.
As a qualitative concept, the spin vector is often handy because it is easy to picture classically. For instance, quantum mechanical spin can exhibit phenomena analogous to classical gyroscopic effects
Gyroscope
A gyroscope is a device for measuring or maintaining orientation, based on the principles of angular momentum. In essence, a mechanical gyroscope is a spinning wheel or disk whose axle is free to take any orientation...
. For example, one can exert a kind of "torque
Torque
Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
" on an electron by putting it in a magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
(the field acts upon the electron's intrinsic magnetic dipole moment—see the following section). The result is that the spin vector undergoes precession
Precession
Precession is a change in the orientation of the rotation axis of a rotating body. It can be defined as a change in direction of the rotation axis in which the second Euler angle is constant...
, just like a classical gyroscope. This phenomenon is used in nuclear magnetic resonance
Nuclear magnetic resonance
Nuclear magnetic resonance is a physical phenomenon in which magnetic nuclei in a magnetic field absorb and re-emit electromagnetic radiation...
sensing.
Mathematically, quantum mechanical spin is not described by vectors as in classical angular momentum, but by objects known as spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
s. There are subtle differences between the behavior of spinors and vectors under coordinate rotations. For example, rotating a spin-1/2 particle by 360 degrees does not bring it back to the same quantum state, but to the state with the opposite quantum phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
; this is detectable, in principle, with interference experiments. To return the particle to its exact original state, one needs a 720 degree rotation. A spin-zero particle can only have a single quantum state, even after torque is applied. Rotating a spin-2 particle 180 degrees can bring it back to the same quantum state and a spin-4 particle should be rotated 90 degrees to bring it back to the same quantum state. The spin 2 particle can be analogous to a straight stick that looks the same even after it is rotated 180 degrees and a spin 0 particle can be imagined as sphere which looks the same after whatever angle it is turned through.
Spin operator
Spin obeys commutation relations analogous to those of the orbital angular momentum: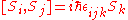
where
 is the Levi-Civita symbol
is the Levi-Civita symbolLevi-Civita symbol
The Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...
. It follows (as with angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
) that the eigenvectors of S2 and Sz (expressed as ket
Bra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
s in the total S basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
) are:


The spin raising and lowering operators
Creation and annihilation operators
Creation and annihilation operators are mathematical operators that have widespread applications in quantum mechanics, notably in the study of quantum harmonic oscillators and many-particle systems. An annihilation operator lowers the number of particles in a given state by one...
acting on these eigenvectors give:
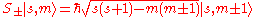 , where
, where 
But unlike orbital angular momentum the eigenvectors are not spherical harmonics
Spherical harmonics
In mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
. They are not functions of θ and φ. There is also no reason to exclude half-integer values of s and m.
In addition to their other properties, all quantum mechanical particles possess an intrinsic spin (though it may have the intrinsic spin 0, too). The spin is quantized in units of the reduced Planck constant, such that the state function of the particle is, e.g., not
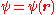 , but
, but 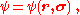 where
where  is out of the following discrete set of values:
is out of the following discrete set of values: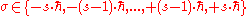 .
.One distinguishes boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s (integer spin) and fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s (half-integer spin). The total angular momentum conserved in interaction processes is then the sum of the orbital angular momentum and the spin.
Pauli matrices and spin operators
The quantum mechanicalQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
operators associated with spin observables are:
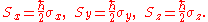
In the special case of spin-1/2
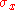 ,
, 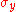 and
and 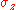 are the three Pauli matrices
are the three Pauli matricesPauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
, given by:
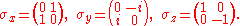
Spin and the Pauli exclusion principle
For systems of N identical particles this is related to the Pauli exclusion principlePauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
, which states that by interchanges of any two of the N particles one must have
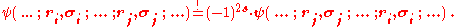
Thus, for bosons the prefactor (−1)2s will reduce to +1, for fermions to −1. In quantum mechanics all particles are either bosons or fermions. In relativistic quantum field theories also "supersymmetric
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
" particles exist, where linear combinations of bosonic and fermionic components appear. In two dimensions, the prefactor (−1)2s can be replaced by any complex number of magnitude 1 (see Anyon
Anyon
In physics, an anyon is a type of particle that occurs only in two-dimensional systems. It is a generalization of the fermion and boson concept.-From theory to reality:...
).
Electrons are fermions with s = 1/2; quanta of light ("photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s") are bosons with s = 1. This shows also explicitly that the property spin cannot be fully explained as a classical intrinsic orbital angular momentum, e.g., similar to that of a "spinning top", since orbital angular rotations would lead to integer values of s. Instead one is dealing with an essential legacy of relativity. The photon, in contrast, is always relativistic (velocity v ≈ c
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
), and the corresponding classical theory, that of Maxwell, is also relativistic.
The above permutation postulate for N-particle state functions has most-important consequences in daily life, e.g. the periodic table
Periodic table
The periodic table of the chemical elements is a tabular display of the 118 known chemical elements organized by selected properties of their atomic structures. Elements are presented by increasing atomic number, the number of protons in an atom's atomic nucleus...
of the chemists or biologists.
Spin and rotations
As described above, quantum mechanics states that component of angular momentum measured along any direction can only take a number of discrete values. The most convenient quantum mechanical description of particle's spin is therefore with a set of complex numbers corresponding to amplitudes of finding a given value of projection of its intrinsic angular momentum on a given axis. For instance, for a spin 1/2 particle, we would need two numbers a±1/2, giving amplitudes of finding it with projection of angular momentum equal to ħ/2 and −ħ/2, satisfying the requirement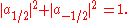
For a generic particle with spin s, we would need 2s+1 such parameters. Since these numbers depend on the choice of the axis, they transform into each other non-trivially when this axis is rotated. It's clear that the transformation law must be linear, so we can represent it by associating a matrix with each rotation, and the product of two transformation matrices corresponding to rotations A and B must be equal (up to phase) to the matrix representing rotation AB. Further, rotations preserve the quantum mechanical inner product, and so should our transformation matrices:
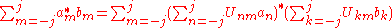
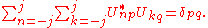
Mathematically speaking, these matrices furnish a unitary projective
Projective representation
In the mathematical field of representation theory, a projective representation of a group G on a vector space V over a field F is a group homomorphism from G to the projective linear groupwhere GL is the general linear group of invertible linear transformations of V over F and F* here is the...
representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of the rotation group
Rotation group
In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
SO(3). Each such representation corresponds to a representation of the covering group of SO(3), which is SU(2). There is one n-dimensional irreducible representation of SU(2) for each dimension, though this representation is n-dimensional real for odd n and n-dimensional complex for even n (hence of real dimension 2n). For a rotation by angle θ in the plane with normal vector
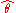 , U can be written
, U can be written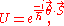
where
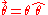 and
and 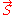 is the vector of spin operators.
is the vector of spin operators.A generic rotation in 3-dimensional space can be built by compounding operators of this type using Euler angles
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
:
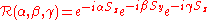
An irreducible representation of this group of operators is furnished by the Wigner D-matrix
Wigner D-matrix
The Wigner D-matrix is a matrix in an irreducible representation of the groups SU and SO. The complex conjugate of the D-matrix is an eigenfunction of the Hamiltonian of spherical and symmetric rigid rotors. The matrix was introduced in 1927 by Eugene Wigner.- Definition Wigner D-matrix :Let j_x,...
:
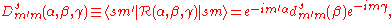
where
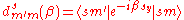
is Wigner's small d-matrix. Note that for γ = 2π and α = β = 0, i.e. a full rotation about the z-axis, the Wigner D-matrix elements become

Recalling that a generic spin state can be written as a superposition of states with definite m, we see that if s is an integer, the values of m are all integers, and this matrix corresponds to the identity operator. However, if s is a half-integer, the values of m are also all half-integers, giving (-1)2m = -1 for all m, and hence upon rotation by 2π the state picks up a minus sign. This fact is a crucial element of the proof of the spin-statistics theorem
Spin-statistics theorem
In quantum mechanics, the spin-statistics theorem relates the spin of a particle to the particle statistics it obeys. The spin of a particle is its intrinsic angular momentum...
.
Spin and Lorentz transformations
We could try the same approach to determine the behavior of spin under general Lorentz transformationLorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
s, but we'd immediately discover a major obstacle. Unlike SO(3), the group of Lorentz transformations SO(3,1) is non-compact
Compact group
In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
and therefore does not have any faithful unitary finite-dimensional representations.
In case of spin 1/2 particles, it is possible to find a construction that includes both a finite-dimensional representation and a scalar product that is preserved by this representation. We associate a 4-component Dirac spinor
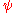 with each particle. These spinors transform under Lorentz transformations according to the law
with each particle. These spinors transform under Lorentz transformations according to the law
where
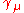 are gamma matrices and
are gamma matrices and  is an antisymmetric 4x4 matrix parametrizing the transformation. It can be shown that the scalar product
is an antisymmetric 4x4 matrix parametrizing the transformation. It can be shown that the scalar product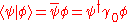
is preserved. (It is not, however, positive definite, so the representation is not unitary.)
Measuring spin along the x, y, and z axes
Each of the (Hermitian) Pauli matrices has two eigenvalues, +1 and −1. The corresponding normalized eigenvectors are:
By the postulates of quantum mechanics, an experiment designed to measure the electron spin on the x, y or z axis can only yield an eigenvalue of the corresponding spin operator (
 or
or  ) on that axis, i.e.
) on that axis, i.e.  or
or 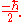 The quantum state of a particle (with respect to spin), can be represented by a two component spinor
The quantum state of a particle (with respect to spin), can be represented by a two component spinorSpinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
:
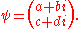
When the spin of this particle is measured with respect to a given axis (in this example, the x-axis), the probability that its spin will be measured as
 is just
is just  . Correspondingly, the probability that its spin will be measured as
. Correspondingly, the probability that its spin will be measured as  is just
is just  . Following the measurement, the spin state of the particle will collapse
. Following the measurement, the spin state of the particle will collapseWavefunction collapse
In quantum mechanics, wave function collapse is the phenomenon in which a wave function—initially in a superposition of several different possible eigenstates—appears to reduce to a single one of those states after interaction with an observer...
into the corresponding eigenstate. As a result, if the particle's spin along a given axis has been measured to have a given eigenvalue, all measurements will yield the same eigenvalue (since
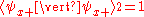 , etc), provided that no measurements of the spin are made along other axes (see compatibility section below).
, etc), provided that no measurements of the spin are made along other axes (see compatibility section below).Measuring spin along an arbitrary axis
The operator to measure spin along an arbitrary axis direction is easily obtained from the Pauli spin matrices. Let be an arbitrary unit vector. Then the operator for spin in this direction is simply
be an arbitrary unit vector. Then the operator for spin in this direction is simply 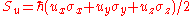 . The operator
. The operator  has eigenvalues of
has eigenvalues of  , just like the usual spin matrices. This method of finding the operator for spin in an arbitrary direction generalizes to higher spin states, one takes the dot product of the direction with a vector of the three operators for the three x,y,z axis directions.
, just like the usual spin matrices. This method of finding the operator for spin in an arbitrary direction generalizes to higher spin states, one takes the dot product of the direction with a vector of the three operators for the three x,y,z axis directions.A normalized spinor for spin-1/2 in the
 direction (which works for all spin states except spin down where it will give 0/0), is:
direction (which works for all spin states except spin down where it will give 0/0), is: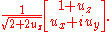
The above spinor is obtained in the usual way by diagonalizing the
 matrix and finding the eigenstates corresponding to the eigenvalues.
matrix and finding the eigenstates corresponding to the eigenvalues.In quantum mechanics, vectors are termed "normalized" when multiplied by a normalizing factor, which results in the vector having a length of unity.
Compatibility of spin measurements
Since the Pauli matrices do not commuteCommutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
, measurements of spin along the different axes are incompatible. This means that if, for example, we know the spin along the x-axis, and we then measure the spin along the y-axis, we have invalidated our previous knowledge of the x-axis spin. This can be seen from the property of the eigenvectors (i.e. eigenstates) of the Pauli matrices that:

So when we measure the spin of a particle along the x-axis as, for example,
 , the particle's spin state collapses
, the particle's spin state collapsesWavefunction collapse
In quantum mechanics, wave function collapse is the phenomenon in which a wave function—initially in a superposition of several different possible eigenstates—appears to reduce to a single one of those states after interaction with an observer...
into the eigenstate
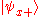 . When we then subsequently measure the particle's spin along the y-axis, the spin state will now collapse into either
. When we then subsequently measure the particle's spin along the y-axis, the spin state will now collapse into either 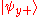 or
or 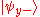 , each with probability
, each with probability  . Let us say, in our example, that we measure
. Let us say, in our example, that we measure 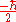 . When we now return to measure the particle's spin along the x-axis again, the probabilities that we will measure
. When we now return to measure the particle's spin along the x-axis again, the probabilities that we will measure  or
or  are each
are each  (i.e. they are
(i.e. they are 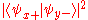 and
and  ). This implies that our original measurement of the spin along the x-axis is no longer valid, since the spin along the x-axis will now be measured to have either eigenvalue with equal probability.
). This implies that our original measurement of the spin along the x-axis is no longer valid, since the spin along the x-axis will now be measured to have either eigenvalue with equal probability.Spin and parity
In tables of the spin quantum number s for nuclei or particles, the spin is often followed by a "+" or "-". This refers to the parityParity (physics)
In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it is also commonly described by the simultaneous flip in the sign of all three spatial coordinates:...
with "+" for even parity (wave function unchanged by spatial inversion) and "-" for odd parity (wave function negated by spatial inversion). For example, see the isotopes of bismuth
Isotopes of bismuth
Bismuth has no stable isotopes, but does have one very long-lived isotope, thus the standard atomic mass can be given. Although bismuth-209 is now known to be unstable, it has classically been considered to be a "stable" isotope because it has a half-life of over 1.9×1019 years, which is...
.
Applications
Spin has important theoretical implications and practical applications. Well-established direct applications of spin include:- Nuclear magnetic resonanceNuclear magnetic resonanceNuclear magnetic resonance is a physical phenomenon in which magnetic nuclei in a magnetic field absorb and re-emit electromagnetic radiation...
spectroscopy in chemistry; - Electron spin resonance spectroscopy in chemistry and physics;
- Magnetic resonance imagingMagnetic resonance imagingMagnetic resonance imaging , nuclear magnetic resonance imaging , or magnetic resonance tomography is a medical imaging technique used in radiology to visualize detailed internal structures...
(MRI) in medicine, which relies on proton spin density; - Giant magnetoresistiveGiant magnetoresistive effectGiant magnetoresistance is a quantum mechanical magnetoresistance effect observed in thin-film structures composed of alternating ferromagnetic and non-magnetic layers...
(GMR) drive head technology in modern hard diskHard diskA hard disk drive is a non-volatile, random access digital magnetic data storage device. It features rotating rigid platters on a motor-driven spindle within a protective enclosure. Data is magnetically read from and written to the platter by read/write heads that float on a film of air above the...
s.
Electron spin plays an important role in magnetism
Magnetism
Magnetism is a property of materials that respond at an atomic or subatomic level to an applied magnetic field. Ferromagnetism is the strongest and most familiar type of magnetism. It is responsible for the behavior of permanent magnets, which produce their own persistent magnetic fields, as well...
, with applications for instance in computer memories. The manipulation of nuclear spin by radiofrequency waves (nuclear magnetic resonance
Nuclear magnetic resonance
Nuclear magnetic resonance is a physical phenomenon in which magnetic nuclei in a magnetic field absorb and re-emit electromagnetic radiation...
) is important in chemical spectroscopy and medical imaging.
Spin-orbit coupling leads to the fine structure
Fine structure
In atomic physics, the fine structure describes the splitting of the spectral lines of atoms due to first order relativistic corrections.The gross structure of line spectra is the line spectra predicted by non-relativistic electrons with no spin. For a hydrogenic atom, the gross structure energy...
of atomic spectra, which is used in atomic clock
Atomic clock
An atomic clock is a clock that uses an electronic transition frequency in the microwave, optical, or ultraviolet region of the electromagnetic spectrum of atoms as a frequency standard for its timekeeping element...
s and in the modern definition of the second
Second
The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
. Precise measurements of the g-factor of the electron have played an important role in the development and verification of quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
. Photon spin is associated with the polarization of light.
A possible future direct application of spin is as a binary information carrier in spin transistor
Spin transistor
The magnetically-sensitive transistor , originally proposed in 1990 and currently still being developed, is an improved design on the common transistor invented in the 1940s...
s. Original concept proposed in 1990 is known as Datta-Das spin transistor. Electronics based on spin transistors is called spintronics
Spintronics
Spintronics , also known as magnetoelectronics, is an emerging technology that exploits both the intrinsic spin of the electron and its associated magnetic moment, in addition to its fundamental electronic charge, in solid-state devices.An additional effect occurs when a spin-polarized current is...
, which includes the manipulation of spins in semiconductor devices.
There are many indirect applications and manifestations of spin and the associated Pauli exclusion principle
Pauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
, starting with the periodic table
Periodic table
The periodic table of the chemical elements is a tabular display of the 118 known chemical elements organized by selected properties of their atomic structures. Elements are presented by increasing atomic number, the number of protons in an atom's atomic nucleus...
of chemistry.
History
Spin was first discovered in the context of the emission spectrumEmission spectrum
The emission spectrum of a chemical element or chemical compound is the spectrum of frequencies of electromagnetic radiation emitted by the element's atoms or the compound's molecules when they are returned to a lower energy state....
of alkali metal
Alkali metal
The alkali metals are a series of chemical elements in the periodic table. In the modern IUPAC nomenclature, the alkali metals comprise the group 1 elements, along with hydrogen. The alkali metals are lithium , sodium , potassium , rubidium , caesium , and francium...
s. In 1924 Wolfgang Pauli introduced what he called a "two-valued quantum degree of freedom" associated with the electron in the outermost shell
Electron shell
An electron shell may be thought of as an orbit followed by electrons around an atom's nucleus. The closest shell to the nucleus is called the "1 shell" , followed by the "2 shell" , then the "3 shell" , and so on further and further from the nucleus. The shell letters K,L,M,.....
. This allowed him to formulate the Pauli exclusion principle
Pauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
, stating that no two electrons can share the same quantum state at the same time.
The physical interpretation of Pauli's "degree of freedom" was initially unknown. Ralph Kronig
Ralph Kronig
Ralph Kronig was a German-American physicist . He is noted for the discovery of particle spin and for his theory of x-ray absorption spectroscopy...
, one of Landé
Alfred Landé
Alfred Landé was a German-American physicist known for his contributions to quantum theory. He is responsible for the Landé g-factor an explanation of the Zeeman Effect.-Life and Achievements:...
's assistants, suggested in early 1925 that it was produced by the self-rotation of the electron. When Pauli heard about the idea, he criticized it severely, noting that the electron's hypothetical surface would have to be moving faster than the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in order for it to rotate quickly enough to produce the necessary angular momentum. This would violate the theory of relativity
Theory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
. Largely due to Pauli's criticism, Kronig decided not to publish his idea.
In the autumn of 1925, the same thought came to two Dutch physicists, George Uhlenbeck and Samuel Goudsmit. Under the advice of Paul Ehrenfest
Paul Ehrenfest
Paul Ehrenfest was an Austrian and Dutch physicist, who made major contributions to the field of statistical mechanics and its relations with quantum mechanics, including the theory of phase transition and the Ehrenfest theorem.- Biography :Paul Ehrenfest was born and grew up in Vienna in a Jewish...
, they published their results. It met a favorable response, especially after Llewellyn Thomas
Llewellyn Thomas
Llewellyn Hilleth Thomas was a British physicist and applied mathematician. He is best known for his contributions to atomic physics, in particular:...
managed to resolve a factor-of-two discrepancy between experimental results and Uhlenbeck and Goudsmit's calculations (and Kronig's unpublished ones). This discrepancy was due to the orientation of the electron's tangent frame, in addition to its position.
Mathematically speaking, a fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
description is needed. The tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
effect is additive and relativistic; that is, it vanishes if c goes to infinity. It is one half of the value obtained without regard for the tangent space orientation, but with opposite sign. Thus the combined effect differs from the latter by a factor two (Thomas precession
Thomas precession
In physics the Thomas precession, named after Llewellyn Thomas, is a special relativistic correction that applies to the spin of an elementary particle or the rotation of a macroscopic gyroscope and relates the angular velocity of the spin of a particle following a curvilinear orbit to the angular...
).
Despite his initial objections, Pauli formalized the theory of spin in 1927, using the modern theory of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
discovered by Schrödinger
Erwin Schrödinger
Erwin Rudolf Josef Alexander Schrödinger was an Austrian physicist and theoretical biologist who was one of the fathers of quantum mechanics, and is famed for a number of important contributions to physics, especially the Schrödinger equation, for which he received the Nobel Prize in Physics in 1933...
and Heisenberg
Werner Heisenberg
Werner Karl Heisenberg was a German theoretical physicist who made foundational contributions to quantum mechanics and is best known for asserting the uncertainty principle of quantum theory...
. He pioneered the use of Pauli matrices
Pauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
as a representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of the spin operators, and introduced a two-component spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
wave-function.
Pauli's theory of spin was non-relativistic. However, in 1928, Paul Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
published the Dirac equation
Dirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
, which described the relativistic electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
. In the Dirac equation, a four-component spinor (known as a "Dirac spinor") was used for the electron wave-function. In 1940, Pauli proved the spin-statistics theorem
Spin-statistics theorem
In quantum mechanics, the spin-statistics theorem relates the spin of a particle to the particle statistics it obeys. The spin of a particle is its intrinsic angular momentum...
, which states that fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s have half-integer spin and boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s integer spin.
In retrospect, the first direct experimental evidence of the electron spin was the Stern-Gerlach experiment of 1922. However, the correct explanation of this experiment was only given in 1927.
External links
- "Spintronics. Feature Article" in Scientific AmericanScientific AmericanScientific American is a popular science magazine. It is notable for its long history of presenting science monthly to an educated but not necessarily scientific public, through its careful attention to the clarity of its text as well as the quality of its specially commissioned color graphics...
, June 2002. - Goudsmit on the discovery of electron spin.
- NatureNatureNature, in the broadest sense, is equivalent to the natural world, physical world, or material world. "Nature" refers to the phenomena of the physical world, and also to life in general...
: " Milestones in 'spin' since 1896." - ECE 495N Lecture 36: Spin Online lecture by S. Datta

