
Conjugacy class
Encyclopedia
In mathematics
, especially group theory
, the elements of any group
may be partitioned
into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure. In all abelian group
s every conjugacy class is a set containing one element (singleton set).
Function
s that are constant for members of the same conjugacy class are called class function
s.
(In linear algebra
, this is referred to as similarity of matrices.)
It can be readily shown that conjugacy is an equivalence relation
and therefore partitions G into equivalence classes. (This means that every element of the group belongs to precisely one conjugacy class, and the classes Cl(a) and Cl(b) are equal if and only if
a and b are conjugate, and disjoint otherwise.) The equivalence class that contains the element a in G is
and is called the conjugacy class of a. The class number of G is the number of distinct (nonequivalent) conjugacy classes.
Conjugacy classes may be referred to by describing them, or more briefly by abbreviations such as "6A", meaning "a certain conjugacy class of order 6 elements", and "6B" would be a different conjugacy class of order 6 elements; the conjugacy class 1A is the conjugacy class of the identity. In some cases, conjugacy classes can be described in a uniform way – for example, in the symmetric group they can be described by cycle structure.
S3, consisting of all 6 permutation
s of three elements, has three conjugacy classes:
The symmetric group S4, consisting of all 24 permutations of four elements, has five conjugacy classes, listed with their cycle structures and orders:
In general, the number of conjugacy classes in the symmetric group Sn is equal to the number of integer partitions of n. This is because each conjugacy class corresponds to exactly one partition of {1, 2, ..., n} into cycles
, up to permutation of the elements of {1, 2, ..., n}.
See also the proper rotations of the cube, which can be characterized by permutations of the body diagonals.
, then for any group element a, the elements in the conjugacy class of a are in one-to-one correspondence with coset
s of the centralizer CG(a). This can be seen by observing that any two elements b and c belonging to the same coset (and hence, b=cz for some z in the centralizer CG(a)) give rise to the same element when conjugating a: bab−1=cza(cz)−1=czaz-1c-1=czz-1ac-1=cac−1.
Thus the number of elements in the conjugacy class of a is the index
[G:CG(a)] of the centralizer CG(a) in G. Lagrange's theorem
then implies that the size of each conjugacy class is a divisor of the order of the group.
Furthermore, if we choose a single representative element xi from every conjugacy class, we infer from the disjointedness of the conjugacy classes that |G| = ∑i [G : CG(xi)], where CG(xi) is the centralizer of the element xi. Observing that each element of the center Z(G) forms a conjugacy class containing just itself gives rise to the following important class equation:
where the second sum is over a representative element from each conjugacy class that is not in the center.
Knowledge of the divisors of the group order |G| can often be used to gain information about the order of the center or of the conjugacy classes.
G (that is, a group with order pn, where p is a prime number
and n > 0). We are going to prove that: every finite p-group has a non-trivial
center.
Since the order of any conjugacy class of G must divide the order of G, it follows that each conjugacy class Hi also has order some power of p(ki), where 0 < ki < n. But then the class equation requires that |G| = pn = |Z(G)| + ∑i (p(ki)). From this we see that p must divide |Z(G)|, so |Z(G)| > 1.
S of G (S not necessarily a subgroup), we define a subset T of G to be conjugate to S if and only if
there exists some g in G such that T = gSg−1. We can define Cl(S) as the set of all subsets T of G such that T is conjugate to S.
A frequently used theorem is that, given any subset S of G, the index
of N(S) (the normalizer of S) in G equals the order of Cl(S):
This follows since, if g and h are in G, then gSg−1 = hSh−1 if and only if g−1h is in N(S), in other words, if and only if g and h are in the same coset
of N(S).
Note that this formula generalizes the one given earlier for the number of elements in a conjugacy class (let S = {a}).
The above is particularly useful when talking about subgroups of G. The subgroups can thus be divided into conjugacy classes, with two subgroups belonging to the same class if and only if they are conjugate.
Conjugate subgroups are isomorphic
, but isomorphic subgroups need not be conjugate (for example, an abelian group may have two different subgroups which are isomorphic, but they are never conjugate).
for any two elements g and x in G, then we have a group action
of G on G. The orbits of this action are the conjugacy classes, and the stabilizer of a given element is the element's centralizer.
Similarly, we can define a group action of G on the set of all subsets of G, by writing
or on the set of the subgroups of G.
of a path-connected topological space can be thought of as equivalence classes of free loop
s under free homotopy.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, the elements of any group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
may be partitioned
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure. In all abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s every conjugacy class is a set containing one element (singleton set).
Function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s that are constant for members of the same conjugacy class are called class function
Class function
In mathematics, especially in the fields of group theory and representation theory of groups, a class function is a function f on a group G, such that f is constant on the conjugacy classes of G. In other words, f is invariant under the conjugation map on G...
s.
Definition
Suppose G is a group. Two elements a and b of G are called conjugate if there exists an element g in G with- gag−1 = b.
(In linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, this is referred to as similarity of matrices.)
It can be readily shown that conjugacy is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
and therefore partitions G into equivalence classes. (This means that every element of the group belongs to precisely one conjugacy class, and the classes Cl(a) and Cl(b) are equal if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
a and b are conjugate, and disjoint otherwise.) The equivalence class that contains the element a in G is
- Cl(a) = { gag−1: g ∈ G }
and is called the conjugacy class of a. The class number of G is the number of distinct (nonequivalent) conjugacy classes.
Conjugacy classes may be referred to by describing them, or more briefly by abbreviations such as "6A", meaning "a certain conjugacy class of order 6 elements", and "6B" would be a different conjugacy class of order 6 elements; the conjugacy class 1A is the conjugacy class of the identity. In some cases, conjugacy classes can be described in a uniform way – for example, in the symmetric group they can be described by cycle structure.
Examples
The symmetric groupSymmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
S3, consisting of all 6 permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s of three elements, has three conjugacy classes:
- no change (abc → abc)
- interchanging two (abc → acb, abc → bac, abc → cba)
- a cyclic permutation of all three (abc → bca, abc → cab)
The symmetric group S4, consisting of all 24 permutations of four elements, has five conjugacy classes, listed with their cycle structures and orders:
- (1)4: no change (1 element)
- (2): interchanging two (6 elements)
- (3): a cyclic permutation of three (8 elements)
- (4): a cyclic permutation of all four (6 elements)
- (2)(2): interchanging two, and also the other two (3 elements)
In general, the number of conjugacy classes in the symmetric group Sn is equal to the number of integer partitions of n. This is because each conjugacy class corresponds to exactly one partition of {1, 2, ..., n} into cycles
Cycle notation
In combinatorial mathematics, the cycle notation is a useful convention for writing down a permutation in terms of its constituent cycles. This is also called circular notation and the permutation called a cyclic or circular permutation....
, up to permutation of the elements of {1, 2, ..., n}.
See also the proper rotations of the cube, which can be characterized by permutations of the body diagonals.
Properties
- The identity element is always in its own class, that is Cl(e) = {e}
- If G is abelianAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
, then gag−1 = a for all a and g in G; so Cl(a) = {a} for all a in G; the concept is therefore not very useful in the abelian case. The failure of this thus gives us an idea in what degree the group is nonabelian.
- If two elements a and b of G belong to the same conjugacy class (i.e., if they are conjugate), then they have the same orderOrder (group theory)In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
. More generally, every statement about a can be translated into a statement about b=gag−1, because the map φ(x) = gxg−1 is an automorphismGroup isomorphismIn abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
of G.
- An element a of G lies in the center Z(G) of G if and only if its conjugacy class has only one element, a itself. More generally, if CG(a) denotes the centralizer of a in G, i.e., the subgroupSubgroupIn group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
consisting of all elements g such that ga = ag, then the indexIndex of a subgroupIn mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
[G : CG(a)] is equal to the number of elements in the conjugacy class of a (by the orbit-stabilizer theorem).
- If a and b are conjugate, then so are powers of them,
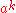 and
and  – thus taking kth powers gives a map on conjugacy classes, and one may speak of which conjugacy classes a given conjugacy class "powers up" into. For example, in the symmetric group, the square of an element of type (3)(2) (a 3-cycle and a 2-cycle) is an element of type (3), while the cube is an element of type (2), so the class (3)(2) powers up into the classes (3) and (2).
– thus taking kth powers gives a map on conjugacy classes, and one may speak of which conjugacy classes a given conjugacy class "powers up" into. For example, in the symmetric group, the square of an element of type (3)(2) (a 3-cycle and a 2-cycle) is an element of type (3), while the cube is an element of type (2), so the class (3)(2) powers up into the classes (3) and (2).
Conjugacy class equation
If G is a finite groupFinite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
, then for any group element a, the elements in the conjugacy class of a are in one-to-one correspondence with coset
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s of the centralizer CG(a). This can be seen by observing that any two elements b and c belonging to the same coset (and hence, b=cz for some z in the centralizer CG(a)) give rise to the same element when conjugating a: bab−1=cza(cz)−1=czaz-1c-1=czz-1ac-1=cac−1.
Thus the number of elements in the conjugacy class of a is the index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
[G:CG(a)] of the centralizer CG(a) in G. Lagrange's theorem
Lagrange's theorem (group theory)
Lagrange's theorem, in the mathematics of group theory, states that for any finite group G, the order of every subgroup H of G divides the order of G. The theorem is named after Joseph Lagrange....
then implies that the size of each conjugacy class is a divisor of the order of the group.
Furthermore, if we choose a single representative element xi from every conjugacy class, we infer from the disjointedness of the conjugacy classes that |G| = ∑i [G : CG(xi)], where CG(xi) is the centralizer of the element xi. Observing that each element of the center Z(G) forms a conjugacy class containing just itself gives rise to the following important class equation:
- |G| = |Z(G)| + ∑i [G : CG(xi)]
where the second sum is over a representative element from each conjugacy class that is not in the center.
Knowledge of the divisors of the group order |G| can often be used to gain information about the order of the center or of the conjugacy classes.
Example
Consider a finite p-groupP-group
In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
G (that is, a group with order pn, where p is a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
and n > 0). We are going to prove that: every finite p-group has a non-trivial
Trivial (mathematics)
In mathematics, the adjective trivial is frequently used for objects that have a very simple structure...
center.
Since the order of any conjugacy class of G must divide the order of G, it follows that each conjugacy class Hi also has order some power of p(ki), where 0 < ki < n. But then the class equation requires that |G| = pn = |Z(G)| + ∑i (p(ki)). From this we see that p must divide |Z(G)|, so |Z(G)| > 1.
Conjugacy of subgroups and general subsets
More generally, given any subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
S of G (S not necessarily a subgroup), we define a subset T of G to be conjugate to S if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
there exists some g in G such that T = gSg−1. We can define Cl(S) as the set of all subsets T of G such that T is conjugate to S.
A frequently used theorem is that, given any subset S of G, the index
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
of N(S) (the normalizer of S) in G equals the order of Cl(S):
- |Cl(S)| = [G : N(S)]
This follows since, if g and h are in G, then gSg−1 = hSh−1 if and only if g−1h is in N(S), in other words, if and only if g and h are in the same coset
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
of N(S).
Note that this formula generalizes the one given earlier for the number of elements in a conjugacy class (let S = {a}).
The above is particularly useful when talking about subgroups of G. The subgroups can thus be divided into conjugacy classes, with two subgroups belonging to the same class if and only if they are conjugate.
Conjugate subgroups are isomorphic
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
, but isomorphic subgroups need not be conjugate (for example, an abelian group may have two different subgroups which are isomorphic, but they are never conjugate).
Conjugacy as group action
If we define- g . x = gxg−1
for any two elements g and x in G, then we have a group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of G on G. The orbits of this action are the conjugacy classes, and the stabilizer of a given element is the element's centralizer.
Similarly, we can define a group action of G on the set of all subsets of G, by writing
- g . S = gSg−1,
or on the set of the subgroups of G.
Geometric interpretation
Conjugacy classes in the fundamental groupFundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of a path-connected topological space can be thought of as equivalence classes of free loop
Free loop
In the mathematical field of topology, a free loop is a variant of the mathematical notion of a loop. Whereas a loop has a distinguished point on it, called a basepoint, a free loop lacks such a distinguished point. Formally, let X be a topological space. Then a free loop in X is an equivalence...
s under free homotopy.

