Conjugate (algebra)
Encyclopedia
In algebra
, a conjugate of an element in a quadratic extension field of a field K is its image under the unique non-identity automorphism
of the extended field that fixes K. If the extension is generated by a square root of an element
r of K, then the conjugate of
is 
for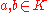 
. In the case of the field C of complex number
s, the complex conjugate
of a+bi is a-bi.
Forming the sum or product of any element of the extension field with its conjugate always gives an element of K. This can be used to rewrite a quotient of numbers in the extended field so that the denominator lies in K, by multiplying numerator and denominator by the conjugate of the denominator. This process is called rationalization
of the denominator, in particular if K is the field Q of rational numbers.
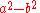
can be factored to give
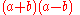
where one factor is the conjugate of the other.
This can be useful when trying to rationalize a denominator containing a radical.
can be made rational by multiplying numerator and denominator by the conjugate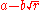 
, so that the denominator becomes 
.
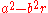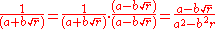
Here is an example:
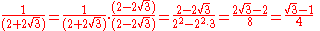
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, a conjugate of an element in a quadratic extension field of a field K is its image under the unique non-identity automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
of the extended field that fixes K. If the extension is generated by a square root of an element
r of K, then the conjugate of
is for 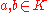. In the case of the field C of complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, the complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
of a+bi is a-bi.
Forming the sum or product of any element of the extension field with its conjugate always gives an element of K. This can be used to rewrite a quotient of numbers in the extended field so that the denominator lies in K, by multiplying numerator and denominator by the conjugate of the denominator. This process is called rationalization
Rationalisation (mathematics)
In elementary algebra, root rationalisation is a process by which surds in the denominator of an irrational fraction are eliminated.These surds may be monomials or binomials involving square roots, in simple examples...
of the denominator, in particular if K is the field Q of rational numbers.
Differences of squares
An expression of the form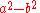can be factored to give
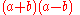
where one factor is the conjugate of the other.
This can be useful when trying to rationalize a denominator containing a radical.
Rationalizing radicals in the denominator
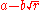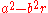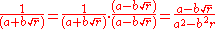
An irrational denominator of the form can be made rational by multiplying numerator and denominator by the conjugate , so that the denominator becomes .Here is an example:
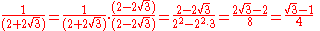
External links
- Rationalizing the Denominator from Mathwords.com
- Math glossary from Bethany Lutheran College