
Clifford algebra
Encyclopedia
In mathematics
, Clifford algebras are a type of associative algebra
. As K-algebras
, they generalize the real number
s, complex number
s, quaternion
s and several other hypercomplex number
systems. The theory of Clifford algebras is intimately connected with the theory of quadratic form
s and orthogonal transformation
s. Clifford algebras have important applications in a variety of fields including geometry
and theoretical physics
. They are named after the English geometer William Kingdon Clifford
.
V equipped with a quadratic form
Q. The Clifford algebra Cℓ(V,Q) is the "freest" algebra generated by V subject to the condition
The definition of a Clifford algebra endows it with more structure than a "bare" K-algebra
, specifically it has a designated or privileged subspace that is isomorphic to V. Such a subspace cannot in general be uniquely determined given only a K-algebra isomorphic to the Clifford algebra.
If the characteristic
of the ground field
K is not 2, then one can rewrite this fundamental identity in the form

where is the symmetric bilinear form associated with Q, via the polarization identity
. The idea of being the "freest" or "most general" algebra subject to this identity can be formally expressed through the notion of a universal property
, as done below.
Quadratic forms and Clifford algebras in characteristic
2 form an exceptional case. In particular, if it is not true that a quadratic form determines a symmetric bilinear form, or that every quadratic form admits an orthogonal basis. Many of the statements in this article include the condition that the characteristic is not 2, and are false if this condition is removed.
s. In fact, if then the Clifford algebra Cℓ(V,Q) is just the exterior algebra Λ(V). For nonzero Q there exists a canonical linear isomorphism between Λ(V) and Cℓ(V,Q) whenever the ground field K does not have characteristic two. That is, they are naturally isomorphic as vector spaces, but with different multiplications (in the case of characteristic two, they are still isomorphic as vector spaces, just not naturally). Clifford multiplication together with the privileged subspace is strictly richer than the exterior product since it makes use of the extra information provided by Q.
More precisely, Clifford algebras may be thought of as quantizations (cf. quantization (physics)
, Quantum group
) of the exterior algebra, in the same way that the Weyl algebra is a quantization of the symmetric algebra
.
Weyl algebras and Clifford algebras admit a further structure of a *-algebra, and can be unified as even and odd terms of a superalgebra
, as discussed in CCR and CAR algebras
.
over a field
K, and let be a quadratic form
on V.
In most cases of interest the field K is either R, C or a finite field
.
A Clifford algebra Cℓ(V,Q) is a unital associative algebra
over K together with a linear map
satisfying for all defined by the following universal property
: Given any associative algebra A over K and any linear map such that
(where 1A denotes the multiplicative identity of A), there is a unique algebra homomorphism
such that the following diagram commutes
(i.e. such that ):
Working with a symmetric bilinear form ⟨·,·⟩ instead of Q (in characteristic not 2), the requirement on j is
A Clifford algebra as described above always exists and can be constructed as follows: start with the most general algebra that contains V, namely the tensor algebra
T(V), and then enforce the fundamental identity by taking a suitable quotient
. In our case we want to take the two-sided ideal
IQ in T(V) generated by all elements of the form
 for all
for all 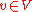
and define Cℓ(V,Q) as the quotient algebra
The ring product inherited by this quotient is sometimes referred to as the Clifford product to differentiate it from the inner and outer products.
It is then straightforward to show that Cℓ(V,Q) contains V and satisfies the above universal property, so that Cℓ is unique up to a unique isomorphism; thus one speaks of "the" Clifford algebra Cℓ(V,Q). It also follows from this construction that i is injective
. One usually drops the i and considers V as a linear subspace
of Cℓ(V,Q).
The universal characterization of the Clifford algebra shows that the construction of Cℓ(V,Q) is functorial in nature. Namely, Cℓ can be considered as a functor
from the category
of vector spaces with quadratic forms (whose morphism
s are linear maps preserving the quadratic form) to the category of associative algebras. The universal property guarantees that linear maps between vector spaces (preserving the quadratic form) extend uniquely to algebra homomorphism
s between the associated Clifford algebras.
of V, then the set

is a basis for Cℓ(V,Q). The empty product is defined as the multiplicative identity element
. For each value of k there are n choose k
basis elements, so the total dimension of the Clifford algebra is
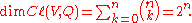
Since V comes equipped with a quadratic form, there is a set of privileged bases for V: the orthogonal ones. An orthogonal basis
is one such that
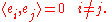
where ⟨·,·⟩ is the symmetric bilinear form associated to Q. The fundamental Clifford identity implies that for an orthogonal basis
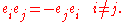
This makes manipulation of orthogonal basis vectors quite simple. Given a product of distinct orthogonal basis vectors of V, one can put them into standard order while including an overall sign determined by the number of pairwise swaps needed to do so (i.e. the signature of the ordering permutation
of distinct orthogonal basis vectors of V, one can put them into standard order while including an overall sign determined by the number of pairwise swaps needed to do so (i.e. the signature of the ordering permutation
).
and complex
vector spaces equipped with nondegenerate quadratic forms. The geometric interpretation of nondegenerate real Clifford algebras is known as geometric algebra
.
Every nondegenerate quadratic form on a finite-dimensional real vector space is equivalent to the standard diagonal form:
where is the dimension of the vector space. The pair of integers (p, q) is called the signature
of the quadratic form. The real vector space with this quadratic form is often denoted Rp,q. The Clifford algebra on Rp,q is denoted Cℓp,q(R).
The symbol
Cℓn(R)
means either
Cℓn,0(R)
or
Cℓ0,n(R)
depending on whether the author prefers positive definite or negative definite spaces.
A standard orthonormal basis
{ei} for Rp,q consists of mutually orthogonal vectors, p of which have norm +1 and q of which have norm −1. The algebra Cℓp,q(R) will therefore have p vectors which square to +1 and q vectors which square to −1.
Note that Cℓ0,0(R) is naturally isomorphic to R since there are no nonzero vectors. Cℓ0,1(R) is a two-dimensional algebra generated by a single vector e1 which squares to −1, and therefore is isomorphic to C, the field of complex number
s. The algebra Cℓ0,2(R) is a four-dimensional algebra spanned by {1, e1, e2, e1e2}. The latter three elements square to −1 and all anticommute, and so the algebra is isomorphic to the quaternion
s H. The next algebra in the sequence is Cℓ0,3(R), and is an 8-dimensional algebra isomorphic to the direct sum called split-biquaternions.
One can also study Clifford algebras on complex vector spaces. Every nondegenerate quadratic form on a complex vector space is equivalent to the standard diagonal form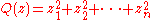
where n = dim V, so there is essentially only one Clifford algebra for each dimension n. We will denote the Clifford algebra on Cn with the standard quadratic form by Cℓn(C). One can show that the algebra Cℓn(C) may be obtained as the complexification
of the algebra Cℓp,q(R) where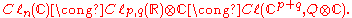
Here Q is the real quadratic form of signature (p,q). Note that the result of the complexification does not depend on the signature. The first few cases are not hard to compute. One finds that
where M2(C) denotes the algebra of 2×2 matrices over C.
It turns out that every one of the algebras Cℓp,q(R) and Cℓn(C) is isomorphic to a matrix algebra
over R, C, or H or to a direct sum of two such algebras. For a complete classification of these algebras see classification of Clifford algebras
.
s are constructed as the even sub algebra of the Clifford algebra Cℓ0,3(R).
Let the vector space V be real three dimensional space R3, and the quadratic form Q be derived from the usual Euclidean metric. Then, for v, w in R3 we have the quadratic form, or dot product,
Now introduce the Clifford product of vectors v and w given by
This formulation uses the negative sign so the correspondence with quaternion
s is easily shown.
Denote a set of orthogonal unit vectors of R3 as e1, e2, and e3, then the Clifford product yields the relations
and
The general element of the Clifford algebra Cℓ0,3(R) is given by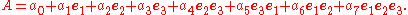
The linear combination of the even rank elements of Cℓ0,3(R) defines the even sub algebra Cℓ00,3(R) with the general element
The basis elements can be identified with the quaternion units i, j, k as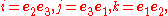
which shows that the even sub algebra Cℓ00,3(R) is Hamilton's real quaternion
algebra.
To see this, compute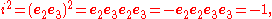
and
Finally,
s are constructed as the even Clifford algebra of real four dimensional space with a degenerate quadratic form.
Let the vector space V be real four dimensional space R4, and let the quadratic form Q be a degenerate form derived from the Euclidean metric on R3. For v, w in R4 introduce the degenerate bilinear form
This degenerate scalar product projects distance measurements in R4 onto the R3 hyperplane.
The Clifford product of vectors v and w is given by
Note the negative sign is introduced to simplify the correspondence with quaternions.
Denote a set of orthogonal unit vectors of R4 as e1, e2, e3 and e4, then the Clifford product yields the relations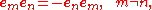
and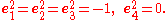
The general element of the Clifford algebra Cℓ(R4,d) has 16 components. The linear combination of the even ranked elements defines the even sub algebra Cℓ0(R4,d) with the general element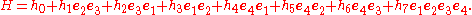
The basis elements can be identified with the quaternion units i, j, k and the dual unit ε as
This provides the correspondence of Cℓ00,3,1(R) with dual quaternion
algebra.
To see this, compute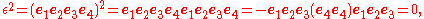
and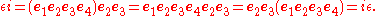
The exchanges of e1 and e4 alternate signs an even number of times, and show the dual unit ε commutes with the quaternion units i, j, and k.
Λ(V), whose definition is independent of any quadratic form on V. It turns out that if K does not have characteristic 2 then there is a natural isomorphism between Λ(V) and Cℓ(V,Q) considered as vector spaces (and there exists an isomorphism in characteristic two, which may not be natural). This is an algebra isomorphism if and only if Q = 0. One can thus consider the Clifford algebra Cℓ(V,Q) as an enrichment (or more precisely, a quantization, cf. the Introduction) of the exterior algebra on V with a multiplication that depends on Q (one can still define the exterior product independent of Q).
The easiest way to establish the isomorphism is to choose an orthogonal basis {ei} for V and extend it to a basis for Cℓ(V,Q) as described above. The map is determined by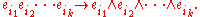
Note that this only works if the basis {ei} is orthogonal. One can show that this map is independent of the choice of orthogonal basis and so gives a natural isomorphism.
If the characteristic
of K is 0, one can also establish the isomorphism by antisymmetrizing. Define functions by
where the sum is taken over the symmetric group
on k elements. Since fk is alternating it induces a unique linear map . The direct sum
of these maps gives a linear map between Λ(V) and Cℓ(V,Q). This map can be shown to be a linear isomorphism, and it is natural.
A more sophisticated way to view the relationship is to construct a filtration
on Cℓ(V,Q). Recall that the tensor algebra
T(V) has a natural filtration: where Fk contains sums of tensors with rank . Projecting this down to the Clifford algebra gives a filtration on Cℓ(V,Q). The associated graded algebra

is naturally isomorphic to the exterior algebra Λ(V). Since the associated graded algebra of a filtered algebra is always isomorphic to the filtered
algebra as filtered vector spaces (by choosing complements of Fk in Fk+1 for all k), this provides an isomorphism (although not a natural one) in any characteristic, even two.
Clifford algebras are Z2-graded algebra
s (also known as superalgebra
s). Indeed, the linear map on V defined by (reflection through the origin) preserves the quadratic form Q and so by the universal property of Clifford algebras extends to an algebra automorphism
(reflection through the origin) preserves the quadratic form Q and so by the universal property of Clifford algebras extends to an algebra automorphism
Since α is an involution (i.e. it squares to the identity
) one can decompose Cℓ(V,Q) into positive and negative eigenspaces of α
where Cℓi(V,Q) = {x ∈ Cℓ(V,Q) | α(x) = (−1)ix}. Since α is an automorphism it follows that
where the superscripts are read modulo 2. This gives Cℓ(V,Q) the structure of a Z2-graded algebra
. The subspace Cℓ0(V,Q) forms a subalgebra
of Cℓ(V,Q), called the even subalgebra. The subspace Cℓ1(V,Q) is called the odd part of Cℓ(V,Q) (it is not a subalgebra). This Z2-grading plays an important role in the analysis and application of Clifford algebras. The automorphism α is called the main involution or grade involution. Elements that are pure in this Z2-grading are simply said to be even or odd.
Remark. In characteristic not 2 the underlying vector space of Cℓ(V,Q) inherits an N-grading and a Z-grading from the canonical isomorphism with the underlying vector space of the exterior algebra Λ(V). It is important to note, however, that this is a vector space grading only. That is, Clifford multiplication does not respect the N-grading or Z-grading, only the Z2-grading: for instance if , then , but , not in . Happily, the gradings are related in the natural way: Z2 ≅N/2N≅ Z/2Z. Further, the Clifford algebra is Z-filtered
:
.
The degree of a Clifford number usually refers to the degree in the N-grading.
The even subalgebra Cℓ0(V,Q) of a Clifford algebra is itself isomorphic to a Clifford algebra.
If V is the orthogonal direct sum of a vector a of norm Q(a) and a subspace U,
then Cℓ0(V,Q) is isomorphic to Cℓ(U,−Q(a)Q),
where −Q(a)Q is the form Q restricted to U and multiplied by −Q(a).
In particular over the reals this implies that for q > 0, and
for q > 0, and for p > 0.
for p > 0.
In the negative-definite case this gives an inclusion Cℓ0,n−1(R) ⊂ Cℓ0,n(R) which extends the sequence
Likewise, in the complex case, one can show that the even subalgebra of Cℓn(C) is isomorphic to Cℓn−1(C).
T(V) comes with an antiautomorphism that reverses the order in all products:
Since the ideal IQ is invariant under this reversal, this operation descends to an antiautomorphism of Cℓ(V,Q) called the transpose or reversal operation, denoted by xt. The transpose is an antiautomorphism: . The transpose operation makes no use of the Z2-grading so we define a second antiautomorphism by composing α and the transpose. We call this operation Clifford conjugation denoted
. The transpose operation makes no use of the Z2-grading so we define a second antiautomorphism by composing α and the transpose. We call this operation Clifford conjugation denoted 
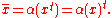
Of the two antiautomorphisms, the transpose is the more fundamental.
Note that all of these operations are involutions. One can show that they act as ±1 on elements which are pure in the Z-grading. In fact, all three operations depend only on the degree modulo 4. That is, if x is pure with degree k then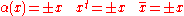
where the signs are given by the following table:

where ⟨a⟩ denotes the scalar part of a (the grade 0 part in the Z-grading). One can show that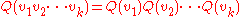
where the vi are elements of V – this identity is not true for arbitrary elements of Cℓ(V,Q).
The associated symmetric bilinear form on Cℓ(V,Q) is given by
One can check that this reduces to the original bilinear form when restricted to V. The bilinear form on all of Cℓ(V,Q) is nondegenerate if and only if it is nondegenerate on V.
It is not hard to verify that the transpose is the adjoint of left/right Clifford multiplication with respect to this inner product. That is, and
and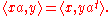
that the bilinear form of Q is non-singular. A central simple algebra
over K
is a matrix algebra over a (finite dimensional) division algebra with center K. For example, the central simple algebras over the reals are matrix algebras over either the reals or the quaternions.
The structure of Clifford algebras can be worked out explicitly using the following result. Suppose that U has even dimension and a non-singular bilinear form with discriminant
d, and suppose that V is another vector space with a quadratic form. The Clifford algebra of U+V is isomorphic to
the tensor product of the Clifford algebras of U and (−1)dim(U)/2dV, which is the space V with its quadratic form multiplied by (−1)dim(U)/2d.
Over the reals, this implies in particular that
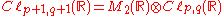

These formulas can be used to find the structure of all real Clifford algebras and all complex Clifford algebras; see the classification of Clifford algebras
.
Notably, the Morita equivalence
class of a Clifford algebra (its representation theory: the equivalence class of the category of modules over it) depends only on the signature . This is an algebraic form of Bott periodicity.
The invertible elements of the Clifford algebra act on it by twisted conjugation: conjugation by x maps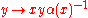 .
.
The Clifford group Γ is defined to be the set of invertible elements x that stabilize vectors, meaning that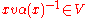
for all v in V.
This formula also defines an action of the Clifford group on the vector space V that preserves the norm Q, and so gives a homomorphism from the Clifford group to the orthogonal group. The Clifford group contains all elements r of V of nonzero norm, and these act on V by the corresponding reflections that take v to (In characteristic 2 these are called orthogonal transvections rather than reflections.)
The Clifford group Γ is the disjoint union of two subsets Γ0 and Γ1, where Γi
is the subset of elements of degree i. The subset Γ0
is a subgroup of index
2 in Γ.
If V is a finite dimensional real vector space with positive definite (or negative definite) quadratic form then the Clifford group maps onto the orthogonal group of V with respect to the form (by the Cartan-Dieudonné theorem
) and the kernel consists of the nonzero elements of the field K. This leads to exact sequences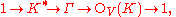

Over other fields or with indefinite forms, the map is not in general onto, and the failure is captured by the spinor norm.

It is a homomorphism from the Clifford group to the group
K* of non-zero elements of K. It coincides with the quadratic form Q of V when V is identified with a subspace of the Clifford algebra.
Several authors define the spinor norm slightly differently, so that it differs from the one here by a factor of −1, 2, or −2 on Γ1. The difference is not very important in characteristic other than 2.
The nonzero elements of K have spinor norm in the group K*2 of squares of nonzero elements of the field K. So when V is finite dimensional and non-singular we get an induced map from the orthogonal group of V to the group K*/K*2, also called the spinor norm. The spinor norm of the reflection of a vector
r has image Q(r) in K*/K*2, and this property uniquely defines it on the orthogonal group. This gives exact sequences:


Note that in characteristic 2 the group {±1} has just one element.
From the point of view of Galois cohomology
of algebraic group
s, the spinor norm is a connecting homomorphism on cohomology. Writing μ2 for the algebraic group of square roots of 1
(over a field of characteristic not 2 it is roughly the same as a two-element group with trivial Galois action), the short exact sequence
yields a long exact sequence on cohomology, which begins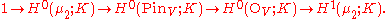
The 0th Galois cohomology group of an algebraic group with coefficients in K is just the group of K-valued points: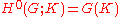 , and
, and  , which recovers the previous sequence
, which recovers the previous sequence
where the spinor norm is the connecting homomorphism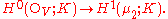
The Pin group
PinV(K) is the subgroup of the
Clifford group Γ of elements of spinor norm 1, and similarly the
Spin group SpinV(K) is the subgroup of elements of Dickson invariant 0 in PinV(K). When the characteristic is not 2, these are the elements of determinant 1. The Spin group usually has index 2 in the Pin group.
Recall from the previous section that there is a homomorphism from the Clifford group onto the orthogonal group. We define the special orthogonal group to be the image of Γ0. If K does not have characteristic 2 this is just the group of elements of the orthogonal group of determinant 1. If K does have characteristic 2, then all elements of the orthogonal group have determinant 1, and the special orthogonal group is the set of elements of Dickson invariant 0.
There is a homomorphism from the Pin group to the orthogonal group. The image consists of the elements of spinor norm 1 ∈ K*/K*2.
The kernel consists of the elements +1 and −1, and has order 2
unless K has characteristic 2. Similarly there is a homomorphism from the Spin group to the special orthogonal group of V.
In the common case when V is a positive or negative definite space over the reals, the spin group maps onto the special orthogonal group, and is simply connected when V has dimension at least 3. Further the kernel of this homomorphism consists of 1 and −1. So in this case the spin group, Spin(n), is a double cover of SO(n). Please note, however, that the simple connectedness of the spin group is not true in general: if V is Rp,q for p and q both at least 2 then the spin group is not simply connected. In this case the algebraic group Spinp,q is simply connected as an algebraic group, even though its group of real valued points Spinp,q(R) is not simply connected. This is a rather subtle point, which completely confused the authors of at least one standard book about spin groups.
representation of dimension 2n. By restricting to the group Pinp,q(R) we get a complex representation of the Pin group
of the same dimension, called the spin representation. If we restrict this to the spin group Spinp,q(R) then it splits as the sum of two half spin representations (or Weyl representations) of dimension 2n−1.
If p+q=2n+1 is odd then the Clifford algebra Cℓp,q(C) is a sum of two matrix algebras, each of which has a representation of dimension 2n, and these are also both representations of the Pin group Pinp,q(R). On restriction to the spin group Spinp,q(R) these become isomorphic, so the spin group has a complex spinor representation of dimension 2n.
More generally, spinor groups and pin groups over any field have similar
representations whose exact structure depends on the structure of the corresponding Clifford algebras
: whenever a Clifford algebra has a factor that
is a matrix algebra over some division algebra, we get a corresponding representation of the pin and spin groups over that division algebra.
For examples over the reals see the article on spinor
s.
, Pinp,q is the set of invertible elements in Cℓp,q which can be written as a product of unit vectors:
Comparing with the above concrete realizations of the Clifford algebras, the Pin group corresponds to the products of arbitrarily many reflections: it is a cover of the full orthogonal group O(p,q). The Spin group consists of those elements of Pinp,q which are products of an even number of unit vectors. Thus by the Cartan-Dieudonné theorem
Spin is a cover of the group of proper rotations SO(p,q).
Let α : Cℓ → Cℓ be the automorphism which is given by the mapping v → −v acting on pure vectors. Then in particular, Spinp,q is the subgroup of Pinp,q whose elements are fixed by α. Let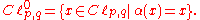
(These are precisely the elements of even degree in Cℓp,q.) Then the spin group lies within Cℓ0p,q.
The irreducible representations of Cℓp,q restrict to give representations of the pin group. Conversely, since the pin group is generated by unit vectors, all of its irreducible representation are induced in this manner. Thus the two representations coincide. For the same reasons, the irreducible representations of the spin coincide with the irreducible representations of Cℓ0p,q
To classify the pin representations, one need only appeal to the classification of Clifford algebras
. To find the spin representations (which are representations of the even subalgebra), one can first make use of either of the isomorphisms (see above)
and realize a spin representation in signature (p,q) as a pin representation in either signature (p,q−1) or (q,p−1).
of differential form
s on a smooth manifold. In the case of a (pseudo
-)Riemannian manifold
, the tangent space
s come equipped with a natural quadratic form induced by the metric
. Thus, one can define a Clifford bundle
in analogy with the exterior bundle
. This has a number of important applications in Riemannian geometry
. Perhaps more importantly is the link to a spin manifold, its associated spinor bundle and spinc manifolds.
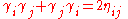
where η is the matrix of a quadratic form of signature (1,3). These are exactly the defining relations for the Clifford algebra Cℓ1,3(C) (up to an unimportant factor of 2),
which by the classification of Clifford algebras
is isomorphic to
the algebra of 4 by 4 complex matrices.
The Dirac matrices were first written down by Paul Dirac
when he was trying to write a relativistic first-order wave equation for the electron
, and give an explicit isomorphism from the Clifford algebra to the algebra of complex matrices. The result was used to define the Dirac equation
and introduce the Dirac operator
. The entire Clifford algebra shows up in quantum field theory
in the form of Dirac field bilinears.
. Rodriguez et al. propose a Clifford embedding to generalize traditional MACH filters to video (3D spatiotemporal volume), and vector-valued data such as optical flow
. Vector-valued data is analyzed using the Clifford Fourier transform. Based on these vectors action filters are synthesized in the Clifford Fourier domain and recognition of actions is performed using Clifford Correlation. The authors demonstrate the effectiveness of the Clifford embedding by recognizing actions typically performed in classic feature films and sports broadcast television.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Clifford algebras are a type of associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
. As K-algebras
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
, they generalize the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s and several other hypercomplex number
Hypercomplex number
In mathematics, a hypercomplex number is a traditional term for an element of an algebra over a field where the field is the real numbers or the complex numbers. In the nineteenth century number systems called quaternions, tessarines, coquaternions, biquaternions, and octonions became established...
systems. The theory of Clifford algebras is intimately connected with the theory of quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s and orthogonal transformation
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
s. Clifford algebras have important applications in a variety of fields including geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
and theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
. They are named after the English geometer William Kingdon Clifford
William Kingdon Clifford
William Kingdon Clifford FRS was an English mathematician and philosopher. Building on the work of Hermann Grassmann, he introduced what is now termed geometric algebra, a special case of the Clifford algebra named in his honour, with interesting applications in contemporary mathematical physics...
.
Introduction and basic properties
Specifically, a Clifford algebra is a unital associative algebra which contains and is generated by a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V equipped with a quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
Q. The Clifford algebra Cℓ(V,Q) is the "freest" algebra generated by V subject to the condition

The definition of a Clifford algebra endows it with more structure than a "bare" K-algebra
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
, specifically it has a designated or privileged subspace that is isomorphic to V. Such a subspace cannot in general be uniquely determined given only a K-algebra isomorphic to the Clifford algebra.
If the characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
of the ground field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K is not 2, then one can rewrite this fundamental identity in the form

where is the symmetric bilinear form associated with Q, via the polarization identity
Polarization identity
In mathematics, the polarization identity is any one of a family of formulas that express the inner product of two vectors in terms of the norm of a normed vector space. Let \|x\| \, denote the norm of vector x and \langle x, \ y \rangle \, the inner product of vectors x and y...
. The idea of being the "freest" or "most general" algebra subject to this identity can be formally expressed through the notion of a universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
, as done below.
Quadratic forms and Clifford algebras in characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
2 form an exceptional case. In particular, if it is not true that a quadratic form determines a symmetric bilinear form, or that every quadratic form admits an orthogonal basis. Many of the statements in this article include the condition that the characteristic is not 2, and are false if this condition is removed.
As a quantization of the exterior algebra
Clifford algebras are closely related to exterior algebraExterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
s. In fact, if then the Clifford algebra Cℓ(V,Q) is just the exterior algebra Λ(V). For nonzero Q there exists a canonical linear isomorphism between Λ(V) and Cℓ(V,Q) whenever the ground field K does not have characteristic two. That is, they are naturally isomorphic as vector spaces, but with different multiplications (in the case of characteristic two, they are still isomorphic as vector spaces, just not naturally). Clifford multiplication together with the privileged subspace is strictly richer than the exterior product since it makes use of the extra information provided by Q.
More precisely, Clifford algebras may be thought of as quantizations (cf. quantization (physics)
Quantization (physics)
In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...
, Quantum group
Quantum group
In mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra...
) of the exterior algebra, in the same way that the Weyl algebra is a quantization of the symmetric algebra
Symmetric algebra
In mathematics, the symmetric algebra S on a vector space V over a field K is the free commutative unital associative algebra over K containing V....
.
Weyl algebras and Clifford algebras admit a further structure of a *-algebra, and can be unified as even and odd terms of a superalgebra
Superalgebra
In mathematics and theoretical physics, a superalgebra is a Z2-graded algebra. That is, it is an algebra over a commutative ring or field with a decomposition into "even" and "odd" pieces and a multiplication operator that respects the grading....
, as discussed in CCR and CAR algebras
CCR and CAR algebras
In Mathematics and Physics the CCR and CAR algebras arise from the study of canonical commutation relations in Bosonic and Fermionic quantum mechanics...
.
Universal property and construction
Let V be a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K, and let be a quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
on V.
In most cases of interest the field K is either R, C or a finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
.
A Clifford algebra Cℓ(V,Q) is a unital associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
over K together with a linear map
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
satisfying for all defined by the following universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
: Given any associative algebra A over K and any linear map such that
- j(v)2 = Q(v)1A for all v ∈ V
(where 1A denotes the multiplicative identity of A), there is a unique algebra homomorphism
Algebra homomorphism
A homomorphism between two algebras, A and B, over a field K, is a map F:A\rightarrow B such that for all k in K and x,y in A,* F = kF* F = F + F...
such that the following diagram commutes
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
(i.e. such that ):
Working with a symmetric bilinear form ⟨·,·⟩ instead of Q (in characteristic not 2), the requirement on j is
- j(v)j(w) + j(w)j(v) = 2⟨v, w⟩ for all
A Clifford algebra as described above always exists and can be constructed as follows: start with the most general algebra that contains V, namely the tensor algebra
Tensor algebra
In mathematics, the tensor algebra of a vector space V, denoted T or T•, is the algebra of tensors on V with multiplication being the tensor product...
T(V), and then enforce the fundamental identity by taking a suitable quotient
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
. In our case we want to take the two-sided ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
IQ in T(V) generated by all elements of the form
 for all
for all 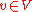
and define Cℓ(V,Q) as the quotient algebra
- Cℓ(V,Q) = T(V)/IQ.
The ring product inherited by this quotient is sometimes referred to as the Clifford product to differentiate it from the inner and outer products.
It is then straightforward to show that Cℓ(V,Q) contains V and satisfies the above universal property, so that Cℓ is unique up to a unique isomorphism; thus one speaks of "the" Clifford algebra Cℓ(V,Q). It also follows from this construction that i is injective
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
. One usually drops the i and considers V as a linear subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of Cℓ(V,Q).
The universal characterization of the Clifford algebra shows that the construction of Cℓ(V,Q) is functorial in nature. Namely, Cℓ can be considered as a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of vector spaces with quadratic forms (whose morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s are linear maps preserving the quadratic form) to the category of associative algebras. The universal property guarantees that linear maps between vector spaces (preserving the quadratic form) extend uniquely to algebra homomorphism
Algebra homomorphism
A homomorphism between two algebras, A and B, over a field K, is a map F:A\rightarrow B such that for all k in K and x,y in A,* F = kF* F = F + F...
s between the associated Clifford algebras.
Basis and dimension
If the dimension of V is n and {e1,…,en} is a basisBasis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
of V, then the set

is a basis for Cℓ(V,Q). The empty product is defined as the multiplicative identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
. For each value of k there are n choose k
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
basis elements, so the total dimension of the Clifford algebra is
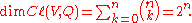
Since V comes equipped with a quadratic form, there is a set of privileged bases for V: the orthogonal ones. An orthogonal basis
Orthogonal basis
In mathematics, particularly linear algebra, an orthogonal basis for an inner product space is a basis for whose vectors are mutually orthogonal...
is one such that
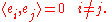
where ⟨·,·⟩ is the symmetric bilinear form associated to Q. The fundamental Clifford identity implies that for an orthogonal basis
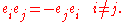
This makes manipulation of orthogonal basis vectors quite simple. Given a product
 of distinct orthogonal basis vectors of V, one can put them into standard order while including an overall sign determined by the number of pairwise swaps needed to do so (i.e. the signature of the ordering permutation
of distinct orthogonal basis vectors of V, one can put them into standard order while including an overall sign determined by the number of pairwise swaps needed to do so (i.e. the signature of the ordering permutationPermutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
).
Examples: real and complex Clifford algebras
The most important Clifford algebras are those over realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
and complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
vector spaces equipped with nondegenerate quadratic forms. The geometric interpretation of nondegenerate real Clifford algebras is known as geometric algebra
Geometric algebra
Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
.
Every nondegenerate quadratic form on a finite-dimensional real vector space is equivalent to the standard diagonal form:

where is the dimension of the vector space. The pair of integers (p, q) is called the signature
Metric signature
The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
of the quadratic form. The real vector space with this quadratic form is often denoted Rp,q. The Clifford algebra on Rp,q is denoted Cℓp,q(R).
The symbol
Cℓn(R)
means either
Cℓn,0(R)
or
Cℓ0,n(R)
depending on whether the author prefers positive definite or negative definite spaces.
A standard orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
{ei} for Rp,q consists of mutually orthogonal vectors, p of which have norm +1 and q of which have norm −1. The algebra Cℓp,q(R) will therefore have p vectors which square to +1 and q vectors which square to −1.
Note that Cℓ0,0(R) is naturally isomorphic to R since there are no nonzero vectors. Cℓ0,1(R) is a two-dimensional algebra generated by a single vector e1 which squares to −1, and therefore is isomorphic to C, the field of complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. The algebra Cℓ0,2(R) is a four-dimensional algebra spanned by {1, e1, e2, e1e2}. The latter three elements square to −1 and all anticommute, and so the algebra is isomorphic to the quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s H. The next algebra in the sequence is Cℓ0,3(R), and is an 8-dimensional algebra isomorphic to the direct sum called split-biquaternions.
One can also study Clifford algebras on complex vector spaces. Every nondegenerate quadratic form on a complex vector space is equivalent to the standard diagonal form
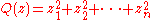
where n = dim V, so there is essentially only one Clifford algebra for each dimension n. We will denote the Clifford algebra on Cn with the standard quadratic form by Cℓn(C). One can show that the algebra Cℓn(C) may be obtained as the complexification
Complexification
In mathematics, the complexification of a real vector space V is a vector space VC over the complex number field obtained by formally extending scalar multiplication to include multiplication by complex numbers. Any basis for V over the real numbers serves as a basis for VC over the complex...
of the algebra Cℓp,q(R) where
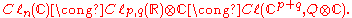
Here Q is the real quadratic form of signature (p,q). Note that the result of the complexification does not depend on the signature. The first few cases are not hard to compute. One finds that
- Cℓ0(C) = C
- Cℓ1(C) = C ⊕ C
- Cℓ2(C) = M2(C)
where M2(C) denotes the algebra of 2×2 matrices over C.
It turns out that every one of the algebras Cℓp,q(R) and Cℓn(C) is isomorphic to a matrix algebra
Matrix algebra
Matrix algebra may refer to:*Matrix theory, is the branch of mathematics that studies matrices*Matrix ring, thought of as an algebra over a field or a commutative ring...
over R, C, or H or to a direct sum of two such algebras. For a complete classification of these algebras see classification of Clifford algebras
Classification of Clifford algebras
In abstract algebra, in particular in the theory of nondegenerate quadratic forms on vector spaces, the structures of finite-dimensional real and complex Clifford algebras have been completely classified...
.
Quaternions
In this section, Hamilton's quaternionQuaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s are constructed as the even sub algebra of the Clifford algebra Cℓ0,3(R).
Let the vector space V be real three dimensional space R3, and the quadratic form Q be derived from the usual Euclidean metric. Then, for v, w in R3 we have the quadratic form, or dot product,
Now introduce the Clifford product of vectors v and w given by

This formulation uses the negative sign so the correspondence with quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s is easily shown.
Denote a set of orthogonal unit vectors of R3 as e1, e2, and e3, then the Clifford product yields the relations

and

The general element of the Clifford algebra Cℓ0,3(R) is given by
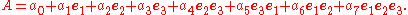
The linear combination of the even rank elements of Cℓ0,3(R) defines the even sub algebra Cℓ00,3(R) with the general element

The basis elements can be identified with the quaternion units i, j, k as
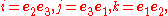
which shows that the even sub algebra Cℓ00,3(R) is Hamilton's real quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
algebra.
To see this, compute
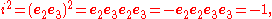
and

Finally,

Dual quaternions
In this section, dual quaternionDual quaternion
The set of dual quaternions is an algebra that can be used to represent spatial rigid body displacements. A dual quaternion is an ordered pair of quaternions  = and therefore is constructed from eight real parameters. Because rigid body displacements are defined by six parameters, dual...
s are constructed as the even Clifford algebra of real four dimensional space with a degenerate quadratic form.
Let the vector space V be real four dimensional space R4, and let the quadratic form Q be a degenerate form derived from the Euclidean metric on R3. For v, w in R4 introduce the degenerate bilinear form
This degenerate scalar product projects distance measurements in R4 onto the R3 hyperplane.
The Clifford product of vectors v and w is given by

Note the negative sign is introduced to simplify the correspondence with quaternions.
Denote a set of orthogonal unit vectors of R4 as e1, e2, e3 and e4, then the Clifford product yields the relations
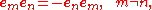
and
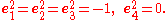
The general element of the Clifford algebra Cℓ(R4,d) has 16 components. The linear combination of the even ranked elements defines the even sub algebra Cℓ0(R4,d) with the general element
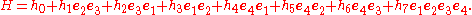
The basis elements can be identified with the quaternion units i, j, k and the dual unit ε as

This provides the correspondence of Cℓ00,3,1(R) with dual quaternion
Dual quaternion
The set of dual quaternions is an algebra that can be used to represent spatial rigid body displacements. A dual quaternion is an ordered pair of quaternions  = and therefore is constructed from eight real parameters. Because rigid body displacements are defined by six parameters, dual...
algebra.
To see this, compute
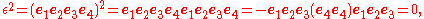
and
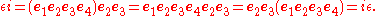
The exchanges of e1 and e4 alternate signs an even number of times, and show the dual unit ε commutes with the quaternion units i, j, and k.
Relation to the exterior algebra
Given a vector space V one can construct the exterior algebraExterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
Λ(V), whose definition is independent of any quadratic form on V. It turns out that if K does not have characteristic 2 then there is a natural isomorphism between Λ(V) and Cℓ(V,Q) considered as vector spaces (and there exists an isomorphism in characteristic two, which may not be natural). This is an algebra isomorphism if and only if Q = 0. One can thus consider the Clifford algebra Cℓ(V,Q) as an enrichment (or more precisely, a quantization, cf. the Introduction) of the exterior algebra on V with a multiplication that depends on Q (one can still define the exterior product independent of Q).
The easiest way to establish the isomorphism is to choose an orthogonal basis {ei} for V and extend it to a basis for Cℓ(V,Q) as described above. The map is determined by
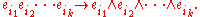
Note that this only works if the basis {ei} is orthogonal. One can show that this map is independent of the choice of orthogonal basis and so gives a natural isomorphism.
If the characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
of K is 0, one can also establish the isomorphism by antisymmetrizing. Define functions by

where the sum is taken over the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on k elements. Since fk is alternating it induces a unique linear map . The direct sum
Direct sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
of these maps gives a linear map between Λ(V) and Cℓ(V,Q). This map can be shown to be a linear isomorphism, and it is natural.
A more sophisticated way to view the relationship is to construct a filtration
Filtration (abstract algebra)
In mathematics, a filtration is an indexed set Si of subobjects of a given algebraic structure S, with the index i running over some index set I that is a totally ordered set, subject to the condition that if i ≤ j in I then Si ⊆ Sj...
on Cℓ(V,Q). Recall that the tensor algebra
Tensor algebra
In mathematics, the tensor algebra of a vector space V, denoted T or T•, is the algebra of tensors on V with multiplication being the tensor product...
T(V) has a natural filtration: where Fk contains sums of tensors with rank . Projecting this down to the Clifford algebra gives a filtration on Cℓ(V,Q). The associated graded algebra
Graded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....

is naturally isomorphic to the exterior algebra Λ(V). Since the associated graded algebra of a filtered algebra is always isomorphic to the filtered
algebra as filtered vector spaces (by choosing complements of Fk in Fk+1 for all k), this provides an isomorphism (although not a natural one) in any characteristic, even two.
Grading
In the following, assume that the characteristic is not 2.Clifford algebras are Z2-graded algebra
Graded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
s (also known as superalgebra
Superalgebra
In mathematics and theoretical physics, a superalgebra is a Z2-graded algebra. That is, it is an algebra over a commutative ring or field with a decomposition into "even" and "odd" pieces and a multiplication operator that respects the grading....
s). Indeed, the linear map on V defined by
 (reflection through the origin) preserves the quadratic form Q and so by the universal property of Clifford algebras extends to an algebra automorphism
(reflection through the origin) preserves the quadratic form Q and so by the universal property of Clifford algebras extends to an algebra automorphismAutomorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
- α : Cℓ(V,Q) → Cℓ(V,Q).
Since α is an involution (i.e. it squares to the identity
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
) one can decompose Cℓ(V,Q) into positive and negative eigenspaces of α

where Cℓi(V,Q) = {x ∈ Cℓ(V,Q) | α(x) = (−1)ix}. Since α is an automorphism it follows that

where the superscripts are read modulo 2. This gives Cℓ(V,Q) the structure of a Z2-graded algebra
Graded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
. The subspace Cℓ0(V,Q) forms a subalgebra
Subalgebra
In mathematics, the word "algebra", when referring to a structure, often means a vector space or module equipped with an additional bilinear operation. Algebras in universal algebra are far more general: they are a common generalisation of all algebraic structures...
of Cℓ(V,Q), called the even subalgebra. The subspace Cℓ1(V,Q) is called the odd part of Cℓ(V,Q) (it is not a subalgebra). This Z2-grading plays an important role in the analysis and application of Clifford algebras. The automorphism α is called the main involution or grade involution. Elements that are pure in this Z2-grading are simply said to be even or odd.
Remark. In characteristic not 2 the underlying vector space of Cℓ(V,Q) inherits an N-grading and a Z-grading from the canonical isomorphism with the underlying vector space of the exterior algebra Λ(V). It is important to note, however, that this is a vector space grading only. That is, Clifford multiplication does not respect the N-grading or Z-grading, only the Z2-grading: for instance if , then , but , not in . Happily, the gradings are related in the natural way: Z2 ≅N/2N≅ Z/2Z. Further, the Clifford algebra is Z-filtered
Filtered algebra
In mathematics, a filtered algebra is a generalization of the notion of a graded algebra. Examples appear in many branches of mathematics, especially in homological algebra and representation theory....
:
.
The degree of a Clifford number usually refers to the degree in the N-grading.
The even subalgebra Cℓ0(V,Q) of a Clifford algebra is itself isomorphic to a Clifford algebra.
If V is the orthogonal direct sum of a vector a of norm Q(a) and a subspace U,
then Cℓ0(V,Q) is isomorphic to Cℓ(U,−Q(a)Q),
where −Q(a)Q is the form Q restricted to U and multiplied by −Q(a).
In particular over the reals this implies that
 for q > 0, and
for q > 0, and for p > 0.
for p > 0.In the negative-definite case this gives an inclusion Cℓ0,n−1(R) ⊂ Cℓ0,n(R) which extends the sequence
- R ⊂ C ⊂ H ⊂ H⊕H ⊂ …
Likewise, in the complex case, one can show that the even subalgebra of Cℓn(C) is isomorphic to Cℓn−1(C).
Antiautomorphisms
In addition to the automorphism α, there are two antiautomorphisms which play an important role in the analysis of Clifford algebras. Recall that the tensor algebraTensor algebra
In mathematics, the tensor algebra of a vector space V, denoted T or T•, is the algebra of tensors on V with multiplication being the tensor product...
T(V) comes with an antiautomorphism that reverses the order in all products:

Since the ideal IQ is invariant under this reversal, this operation descends to an antiautomorphism of Cℓ(V,Q) called the transpose or reversal operation, denoted by xt. The transpose is an antiautomorphism:
 . The transpose operation makes no use of the Z2-grading so we define a second antiautomorphism by composing α and the transpose. We call this operation Clifford conjugation denoted
. The transpose operation makes no use of the Z2-grading so we define a second antiautomorphism by composing α and the transpose. We call this operation Clifford conjugation denoted 
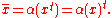
Of the two antiautomorphisms, the transpose is the more fundamental.
Note that all of these operations are involutions. One can show that they act as ±1 on elements which are pure in the Z-grading. In fact, all three operations depend only on the degree modulo 4. That is, if x is pure with degree k then
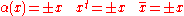
where the signs are given by the following table:
| k mod 4 | 0 | 1 | 2 | 3 | |
|---|---|---|---|---|---|
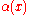 |
+ | − | + | − | (−1)k |
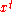 |
+ | + | − | − | (−1)k(k−1)/2 |
 |
+ | − | − | + | (−1)k(k+1)/2 |
The Clifford scalar product
When the characteristic is not 2, the quadratic form Q on V can be extended to a quadratic form on all of Cℓ(V,Q) (which we also denoted by Q). A basis independent definition of one such extension is
where ⟨a⟩ denotes the scalar part of a (the grade 0 part in the Z-grading). One can show that
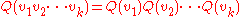
where the vi are elements of V – this identity is not true for arbitrary elements of Cℓ(V,Q).
The associated symmetric bilinear form on Cℓ(V,Q) is given by

One can check that this reduces to the original bilinear form when restricted to V. The bilinear form on all of Cℓ(V,Q) is nondegenerate if and only if it is nondegenerate on V.
It is not hard to verify that the transpose is the adjoint of left/right Clifford multiplication with respect to this inner product. That is,
 and
and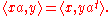
Structure of Clifford algebras
In this section we assume that the vector space V is finite dimensional andthat the bilinear form of Q is non-singular. A central simple algebra
Central simple algebra
In ring theory and related areas of mathematics a central simple algebra over a field K is a finite-dimensional associative algebra A, which is simple, and for which the center is exactly K...
over K
is a matrix algebra over a (finite dimensional) division algebra with center K. For example, the central simple algebras over the reals are matrix algebras over either the reals or the quaternions.
- If V has even dimension then Cℓ(V,Q) is a central simple algebra over K.
- If V has even dimension then Cℓ0(V,Q) is a central simple algebra over a quadratic extension of K or a sum of two isomorphic central simple algebras over K.
- If V has odd dimension then Cℓ(V,Q) is a central simple algebra over a quadratic extension of K or a sum of two isomorphic central simple algebras over K.
- If V has odd dimension then Cℓ0(V,Q) is a central simple algebra over K.
The structure of Clifford algebras can be worked out explicitly using the following result. Suppose that U has even dimension and a non-singular bilinear form with discriminant
Discriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
d, and suppose that V is another vector space with a quadratic form. The Clifford algebra of U+V is isomorphic to
the tensor product of the Clifford algebras of U and (−1)dim(U)/2dV, which is the space V with its quadratic form multiplied by (−1)dim(U)/2d.
Over the reals, this implies in particular that

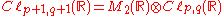

These formulas can be used to find the structure of all real Clifford algebras and all complex Clifford algebras; see the classification of Clifford algebras
Classification of Clifford algebras
In abstract algebra, in particular in the theory of nondegenerate quadratic forms on vector spaces, the structures of finite-dimensional real and complex Clifford algebras have been completely classified...
.
Notably, the Morita equivalence
Morita equivalence
In abstract algebra, Morita equivalence is a relationship defined between rings that preserves many ring-theoretic properties. It is named after Japanese mathematician Kiiti Morita who defined equivalence and a similar notion of duality in 1958.- Motivation :...
class of a Clifford algebra (its representation theory: the equivalence class of the category of modules over it) depends only on the signature . This is an algebraic form of Bott periodicity.
The Clifford group Γ
In this section we assume that V is finite dimensional and the quadratic form Q is nondegenerate.The invertible elements of the Clifford algebra act on it by twisted conjugation: conjugation by x maps
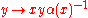 .
.The Clifford group Γ is defined to be the set of invertible elements x that stabilize vectors, meaning that
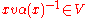
for all v in V.
This formula also defines an action of the Clifford group on the vector space V that preserves the norm Q, and so gives a homomorphism from the Clifford group to the orthogonal group. The Clifford group contains all elements r of V of nonzero norm, and these act on V by the corresponding reflections that take v to (In characteristic 2 these are called orthogonal transvections rather than reflections.)
The Clifford group Γ is the disjoint union of two subsets Γ0 and Γ1, where Γi
is the subset of elements of degree i. The subset Γ0
is a subgroup of index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
2 in Γ.
If V is a finite dimensional real vector space with positive definite (or negative definite) quadratic form then the Clifford group maps onto the orthogonal group of V with respect to the form (by the Cartan-Dieudonné theorem
Cartan-Dieudonné theorem
In mathematics, the Cartan–Dieudonné theorem, named after Élie Cartan and Jean Dieudonné, is a theorem on the structure of the automorphism group of symmetric bilinear spaces.-Statement of the theorem:...
) and the kernel consists of the nonzero elements of the field K. This leads to exact sequences
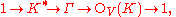

Over other fields or with indefinite forms, the map is not in general onto, and the failure is captured by the spinor norm.
Spinor norm
In arbitrary characteristic, the spinor norm Q is defined on the Clifford group by
It is a homomorphism from the Clifford group to the group
K* of non-zero elements of K. It coincides with the quadratic form Q of V when V is identified with a subspace of the Clifford algebra.
Several authors define the spinor norm slightly differently, so that it differs from the one here by a factor of −1, 2, or −2 on Γ1. The difference is not very important in characteristic other than 2.
The nonzero elements of K have spinor norm in the group K*2 of squares of nonzero elements of the field K. So when V is finite dimensional and non-singular we get an induced map from the orthogonal group of V to the group K*/K*2, also called the spinor norm. The spinor norm of the reflection of a vector
r has image Q(r) in K*/K*2, and this property uniquely defines it on the orthogonal group. This gives exact sequences:


Note that in characteristic 2 the group {±1} has just one element.
From the point of view of Galois cohomology
Galois cohomology
In mathematics, Galois cohomology is the study of the group cohomology of Galois modules, that is, the application of homological algebra to modules for Galois groups...
of algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
s, the spinor norm is a connecting homomorphism on cohomology. Writing μ2 for the algebraic group of square roots of 1
(over a field of characteristic not 2 it is roughly the same as a two-element group with trivial Galois action), the short exact sequence

yields a long exact sequence on cohomology, which begins
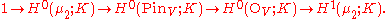
The 0th Galois cohomology group of an algebraic group with coefficients in K is just the group of K-valued points:
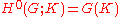 , and
, and  , which recovers the previous sequence
, which recovers the previous sequence
where the spinor norm is the connecting homomorphism
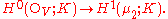
Spin and Pin groups
In this section we assume that V is finite dimensional and its bilinear form is non-singular. (If K has characteristic 2 this implies that the dimension of V is even.)The Pin group
Pin group
In mathematics, the pin group is a certain subgroup of the Clifford algebra associated to a quadratic space. It maps 2-to-1 to the orthogonal group, just as the spin group maps 2-to-1 to the special orthogonal group....
PinV(K) is the subgroup of the
Clifford group Γ of elements of spinor norm 1, and similarly the
Spin group SpinV(K) is the subgroup of elements of Dickson invariant 0 in PinV(K). When the characteristic is not 2, these are the elements of determinant 1. The Spin group usually has index 2 in the Pin group.
Recall from the previous section that there is a homomorphism from the Clifford group onto the orthogonal group. We define the special orthogonal group to be the image of Γ0. If K does not have characteristic 2 this is just the group of elements of the orthogonal group of determinant 1. If K does have characteristic 2, then all elements of the orthogonal group have determinant 1, and the special orthogonal group is the set of elements of Dickson invariant 0.
There is a homomorphism from the Pin group to the orthogonal group. The image consists of the elements of spinor norm 1 ∈ K*/K*2.
The kernel consists of the elements +1 and −1, and has order 2
unless K has characteristic 2. Similarly there is a homomorphism from the Spin group to the special orthogonal group of V.
In the common case when V is a positive or negative definite space over the reals, the spin group maps onto the special orthogonal group, and is simply connected when V has dimension at least 3. Further the kernel of this homomorphism consists of 1 and −1. So in this case the spin group, Spin(n), is a double cover of SO(n). Please note, however, that the simple connectedness of the spin group is not true in general: if V is Rp,q for p and q both at least 2 then the spin group is not simply connected. In this case the algebraic group Spinp,q is simply connected as an algebraic group, even though its group of real valued points Spinp,q(R) is not simply connected. This is a rather subtle point, which completely confused the authors of at least one standard book about spin groups.
Spinors
Clifford algebras Cℓp,q(C), with p+q=2n even, are matrix algebras which have a complexrepresentation of dimension 2n. By restricting to the group Pinp,q(R) we get a complex representation of the Pin group
of the same dimension, called the spin representation. If we restrict this to the spin group Spinp,q(R) then it splits as the sum of two half spin representations (or Weyl representations) of dimension 2n−1.
If p+q=2n+1 is odd then the Clifford algebra Cℓp,q(C) is a sum of two matrix algebras, each of which has a representation of dimension 2n, and these are also both representations of the Pin group Pinp,q(R). On restriction to the spin group Spinp,q(R) these become isomorphic, so the spin group has a complex spinor representation of dimension 2n.
More generally, spinor groups and pin groups over any field have similar
representations whose exact structure depends on the structure of the corresponding Clifford algebras
Classification of Clifford algebras
In abstract algebra, in particular in the theory of nondegenerate quadratic forms on vector spaces, the structures of finite-dimensional real and complex Clifford algebras have been completely classified...
: whenever a Clifford algebra has a factor that
is a matrix algebra over some division algebra, we get a corresponding representation of the pin and spin groups over that division algebra.
For examples over the reals see the article on spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
s.
Real spinors
To describe the real spin representations, one must know how the spin group sits inside its Clifford algebra. The Pin groupPin group
In mathematics, the pin group is a certain subgroup of the Clifford algebra associated to a quadratic space. It maps 2-to-1 to the orthogonal group, just as the spin group maps 2-to-1 to the special orthogonal group....
, Pinp,q is the set of invertible elements in Cℓp,q which can be written as a product of unit vectors:

Comparing with the above concrete realizations of the Clifford algebras, the Pin group corresponds to the products of arbitrarily many reflections: it is a cover of the full orthogonal group O(p,q). The Spin group consists of those elements of Pinp,q which are products of an even number of unit vectors. Thus by the Cartan-Dieudonné theorem
Cartan-Dieudonné theorem
In mathematics, the Cartan–Dieudonné theorem, named after Élie Cartan and Jean Dieudonné, is a theorem on the structure of the automorphism group of symmetric bilinear spaces.-Statement of the theorem:...
Spin is a cover of the group of proper rotations SO(p,q).
Let α : Cℓ → Cℓ be the automorphism which is given by the mapping v → −v acting on pure vectors. Then in particular, Spinp,q is the subgroup of Pinp,q whose elements are fixed by α. Let
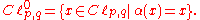
(These are precisely the elements of even degree in Cℓp,q.) Then the spin group lies within Cℓ0p,q.
The irreducible representations of Cℓp,q restrict to give representations of the pin group. Conversely, since the pin group is generated by unit vectors, all of its irreducible representation are induced in this manner. Thus the two representations coincide. For the same reasons, the irreducible representations of the spin coincide with the irreducible representations of Cℓ0p,q
To classify the pin representations, one need only appeal to the classification of Clifford algebras
Classification of Clifford algebras
In abstract algebra, in particular in the theory of nondegenerate quadratic forms on vector spaces, the structures of finite-dimensional real and complex Clifford algebras have been completely classified...
. To find the spin representations (which are representations of the even subalgebra), one can first make use of either of the isomorphisms (see above)
- Cℓ0p,q ≈ Cℓp,q−1, for q > 0
- Cℓ0p,q ≈ Cℓq,p−1, for p > 0
and realize a spin representation in signature (p,q) as a pin representation in either signature (p,q−1) or (q,p−1).
Differential geometry
One of the principal applications of the exterior algebra is in differential geometry where it is used to define the bundleFiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
of differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s on a smooth manifold. In the case of a (pseudo
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
-)Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
, the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
s come equipped with a natural quadratic form induced by the metric
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
. Thus, one can define a Clifford bundle
Clifford bundle
In mathematics, a Clifford bundle is an algebra bundle whose fibers have the structure of a Clifford algebra and whose local trivializations respect the algebra structure...
in analogy with the exterior bundle
Exterior bundle
In mathematics, the exterior bundle of a manifold M is the subbundle of the tensor bundle consisting of all antisymmetric covariant tensors. It has special significance, because one can define a connection-independent derivative on it, namely the exterior derivative.Sections of the exterior bundle...
. This has a number of important applications in Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
. Perhaps more importantly is the link to a spin manifold, its associated spinor bundle and spinc manifolds.
Physics
Clifford algebras have numerous important applications in physics. Physicists usually consider a Clifford algebra to be an algebra spanned by matrices γ0,…,γ3 called Dirac matrices which have the property that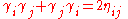
where η is the matrix of a quadratic form of signature (1,3). These are exactly the defining relations for the Clifford algebra Cℓ1,3(C) (up to an unimportant factor of 2),
which by the classification of Clifford algebras
Classification of Clifford algebras
In abstract algebra, in particular in the theory of nondegenerate quadratic forms on vector spaces, the structures of finite-dimensional real and complex Clifford algebras have been completely classified...
is isomorphic to
the algebra of 4 by 4 complex matrices.
The Dirac matrices were first written down by Paul Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
when he was trying to write a relativistic first-order wave equation for the electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
, and give an explicit isomorphism from the Clifford algebra to the algebra of complex matrices. The result was used to define the Dirac equation
Dirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
and introduce the Dirac operator
Dirac operator
In mathematics and quantum mechanics, a Dirac operator is a differential operator that is a formal square root, or half-iterate, of a second-order operator such as a Laplacian...
. The entire Clifford algebra shows up in quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
in the form of Dirac field bilinears.
Computer Vision
Recently, Clifford algebras have been applied in the problem of action recognition and classification in computer visionComputer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
. Rodriguez et al. propose a Clifford embedding to generalize traditional MACH filters to video (3D spatiotemporal volume), and vector-valued data such as optical flow
Optical flow
Optical flow or optic flow is the pattern of apparent motion of objects, surfaces, and edges in a visual scene caused by the relative motion between an observer and the scene. The concept of optical flow was first studied in the 1940s and ultimately published by American psychologist James J....
. Vector-valued data is analyzed using the Clifford Fourier transform. Based on these vectors action filters are synthesized in the Clifford Fourier domain and recognition of actions is performed using Clifford Correlation. The authors demonstrate the effectiveness of the Clifford embedding by recognizing actions typically performed in classic feature films and sports broadcast television.



