Discrete distributions

With finite support

• The Bernoulli distribution, which takes value 1 with probability p and value 0 with probability q = 1 − p.
• The Rademacher distribution, which takes value 1 with probability 1/2 and value −1 with probability 1/2.
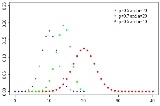
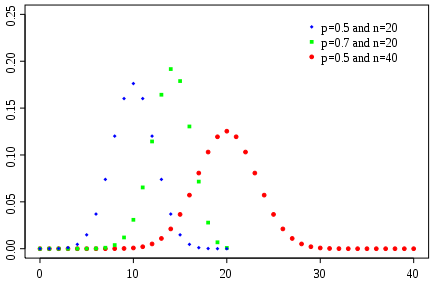
• The binomial distribution, which describes the number of successes in a series of independent Yes/No experiments all with the same probability of success.
• The beta-binomial distribution, which describes the number of successes in a series of independent Yes/No experiments with heterogeneity in the success probability.
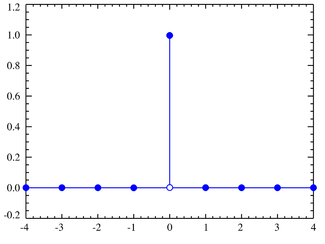
• The degenerate distribution at x₀, where X is certain to take the value x₀. This does not look random, but it satisfies the definition of random variable
  Random variable
  In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
  
  . This is useful because it puts deterministic variables and random variables in the same formalism.
• The discrete uniform distribution, where all elements of a finite set
  Set theory
  Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
  
   are equally likely. This is the theoretical distribution model for a balanced coin, an unbiased die, a casino roulette, or the first card of a well-shuffled deck.
• The hypergeometric distribution, which describes the number of successes in the first m of a series of n consecutive Yes/No experiments, if the total number of successes is known. This distribution arises when there is no replacement.
• The Poisson binomial distribution, which describes the number of successes in a series of independent Yes/No experiments with different success probabilities.
• Fisher's noncentral hypergeometric distribution
  Fisher's noncentral hypergeometric distribution
  In probability theory and statistics, Fisher's noncentral hypergeometric distribution is a generalization of the hypergeometric distribution where sampling probabilities are modified by weight factors...
  
  
• Wallenius' noncentral hypergeometric distribution
  Wallenius' noncentral hypergeometric distribution
  In probability theory and statistics, Wallenius' noncentral hypergeometric distribution is a generalization of the hypergeometric distribution where items are sampled with bias....
  
  

With infinite support

• The beta negative binomial distribution
• The Boltzmann distribution
  Boltzmann distribution
  In chemistry, physics, and mathematics, the Boltzmann distribution is a certain distribution function or probability measure for the distribution of the states of a system. It underpins the concept of the canonical ensemble, providing its underlying distribution...
  
  , a discrete distribution important in statistical physics
  Statistical physics
  Statistical physics is the branch of physics that uses methods of probability theory and statistics, and particularly the mathematical tools for dealing with large populations and approximations, in solving physical problems. It can describe a wide variety of fields with an inherently stochastic...
  
   which describes the probabilities of the various discrete energy levels of a system in thermal equilibrium
  Thermal equilibrium
  Thermal equilibrium is a theoretical physical concept, used especially in theoretical texts, that means that all temperatures of interest are unchanging in time and uniform in space...
  
  . It has a continuous analogue. Special cases include:
  • The Gibbs distribution
  • The Maxwell–Boltzmann distribution
  • The Bose–Einstein distribution
  • The Fermi–Dirac distribution.
• The extended negative binomial distribution
  Extended negative binomial distribution
  In probability and statistics the extended negative binomial distribution is a discrete probability distribution extending the negative binomial distribution. It is a truncated version of the negative binomial distribution for which estimation methods have been studied.In the context of actuarial...
  
  
• The geometric distribution, a discrete distribution which describes the number of attempts needed to get the first success in a series of independent Yes/No experiments.
• The logarithmic (series) distribution
• The negative binomial distribution
  Negative binomial distribution
  In probability theory and statistics, the negative binomial distribution is a discrete probability distribution of the number of successes in a sequence of Bernoulli trials before a specified number of failures occur...
  
  , a generalization of the geometric distribution to the nth success.
• The parabolic fractal distribution
  Parabolic fractal distribution
  In probability and statistics, the parabolic fractal distribution is a type of discrete probability distribution in which the logarithm of the frequency or size of entities in a population is a quadratic polynomial of the logarithm of the rank...
  
  
• The Poisson distribution
  Poisson distribution
  In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
  
  , which describes a very large number of individually unlikely events that happen in a certain time interval.
  • The Conway–Maxwell–Poisson distribution, a two-parameter extension of the Poisson distribution
    Poisson distribution
    In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
    
     with an adjustable rate of decay.
• The Skellam distribution, the distribution of the difference between two independent Poisson-distributed random variables.
• The Yule–Simon distribution
• The zeta distribution has uses in applied statistics and statistical mechanics, and perhaps may be of interest to number theorists. It is the Zipf distribution for an infinite number of elements.
• Zipf's law or the Zipf distribution. A discrete power-law
  Power law
  A power law is a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event , the frequency is said to follow a power law. For instance, the number of cities having a certain population size is found to vary...
  
   distribution, the most famous example of which is the description of the frequency of words in the English language.
• The Zipf–Mandelbrot law is a discrete power law distribution which is a generalization of the Zipf distribution.

Continuous distributions

Supported on a bounded interval

• The Arcsine distribution on [a,b], which is a special case of the Beta distribution if a=0 and b=1.
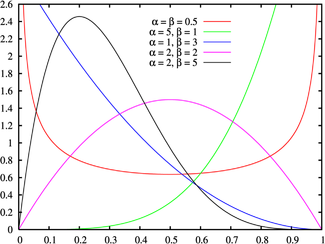
• The Beta distribution on [0,1], of which the uniform distribution is a special case, and which is useful in estimating success probabilities.
• The Logitnormal distribution on (0,1).
• The Dirac delta function
  Dirac delta function
  The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
  
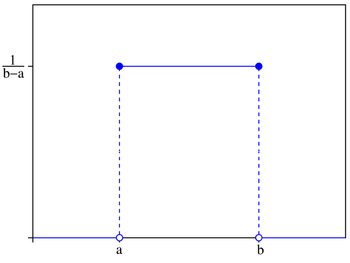
   although not strictly a function, is a limiting form of many continuous probability functions. It represents a discrete probability distribution concentrated at 0 — a degenerate distribution — but the notation treats it as if it were a continuous distribution.
• The continuous uniform distribution
  Uniform distribution (continuous)
  In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
  
   on [a,b], where all points in a finite interval are equally likely.
  • The rectangular distribution is a uniform distribution on [-1/2,1/2].
• The Irwin-Hall distribution
  Irwin-Hall distribution
  In probability and statistics, the Irwin–Hall distribution, named after Joseph Oscar Irwin and Philip Hall, is probability distribution for a random variable defined as sum of a number of independent random variables, each having a uniform distribution...
  
   is the distribution of the sum of n i.i.d. U(0,1) random variables.
• The Kent distribution on the three-dimensional sphere.
• The Kumaraswamy distribution
  Kumaraswamy distribution
  In probability and statistics, the Kumaraswamy's double bounded distribution is a family of continuous probability distributions defined on the interval [0,1] differing in the values of their two non-negative shape parameters, a and b....
  
   is as versatile as the Beta distribution but has simple closed forms for both the cdf and the pdf.
• The logarithmic distribution (continuous)
• The raised cosine distribution on [].
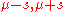• The triangular distribution on [a, b], a special case of which is the distribution of the sum of two independent uniformly distributed random variables (the convolution of two uniform distributions).
• The truncated normal distribution
  Truncated normal distribution
  In probability and statistics, the truncated normal distribution is the probability distribution of a normally distributed random variable whose value is either bounded below or above . The truncated normal distribution has wide applications in statistics and econometrics...
  
   on [a, b].
• The U-quadratic distribution
  U-quadratic distribution
  In probability theory and statistics, the U-quadratic distribution is a continuous probability distribution defined by a unique quadratic function with lower limit a and upper limit b.-Parameter relations:...
  
   on [a, b].
• The von Mises distribution on the circle.
• The von Mises-Fisher distribution on the N-dimensional sphere has the von Mises distribution as a special case.
• The Wigner semicircle distribution is important in the theory of random matrices.

Supported on semi-infinite intervals, usually [0,∞)

• The Beta prime distribution
• The chi distribution
  • The noncentral chi distribution
• The chi-squared distribution, which is the sum of the squares of n independent Gaussian random variables. It is a special case of the Gamma distribution, and it is used in goodness-of-fit tests in statistics
  Statistics
  Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
  
  .
  • The inverse-chi-squared distribution
  • The noncentral chi-squared distribution
  • The Scaled-inverse-chi-squared distribution
• The Dagum distribution
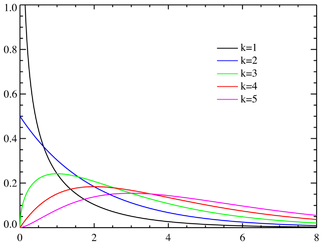
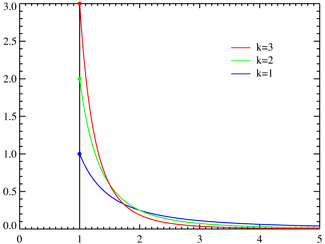
• The exponential distribution
  Exponential distribution
  In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
  
  , which describes the time between consecutive rare random events in a process with no memory.
• The F-distribution, which is the distribution of the ratio of two (normalized) chi-squared distributed random variables, used in the analysis of variance
  Analysis of variance
  In statistics, analysis of variance is a collection of statistical models, and their associated procedures, in which the observed variance in a particular variable is partitioned into components attributable to different sources of variation...
  
  . It is referred to as the beta prime distribution when it is the ratio of two chi-squared variates which are not normalized by dividing them by their numbers of degrees of freedom.
  • The noncentral F-distribution
    Noncentral F-distribution
    In probability theory and statistics, the noncentral F-distribution is a continuous probability distribution that is a generalization of the F-distribution...
    
    
• Fisher's z-distribution
• The folded normal distribution
  Folded Normal Distribution
  The folded normal distribution is a probability distribution related to the normal distribution. Given a normally distributed random variable X with mean μ and variance σ2, the random variable Y = |X| has a folded normal distribution. Such a case may be encountered if only the magnitude of some...
  
  
• The Gamma distribution, which describes the time until n consecutive rare random events occur in a process with no memory.
  • The Erlang distribution, which is a special case of the gamma distribution with integral shape parameter, developed to predict waiting times in queuing systems
  • The inverse-gamma distribution
• The half-normal distribution
  Half-normal distribution
  The half-normal distribution is the probability distribution of the absolute value of a random variable that is normally distributed with expected value 0 and variance σ2. I.e...
  
  
• Hotelling's T-squared distribution
• The inverse Gaussian distribution
  Inverse Gaussian distribution
  | cdf = \Phi\left +\exp\left \Phi\left...
  
  , also known as the Wald distribution
• The Lévy distribution
• The log-Cauchy distribution
  Log-Cauchy distribution
  In probability theory, a log-Cauchy distribution is a probability distribution of a random variable whose logarithm is distributed in accordance with a Cauchy distribution...
  
  
• The log-Laplace distribution
  Log-Laplace distribution
  In probability theory and statistics, the log-Laplace distribution is the probability distribution of a random variable whose logarithm has a Laplace distribution. If X has a Laplace distribution with parameters μ and b, then Y = eX has a log-Laplace distribution...
  
  
• The log-logistic distribution
  Log-logistic distribution
  In probability and statistics, the log-logistic distribution is a continuous probability distribution for a non-negative random variable. It is used in survival analysis as a parametric model for events whose rate increases initially and decreases later, for example mortality from cancer following...
  
  
• The log-normal distribution, describing variables which can be modelled as the product of many small independent positive variables.
• The Mittag–Leffler distribution
• The Pareto distribution, or "power law" distribution, used in the analysis of financial data and critical behavior.
• The Pearson Type III distribution
  Pearson distribution
  The Pearson distribution is a family of continuous probability distributions. It was first published by Karl Pearson in 1895 and subsequently extended by him in 1901 and 1916 in a series of articles on biostatistics.- History :...
  
  
• The Rayleigh distribution
• The Rayleigh mixture distribution
• The Rice distribution
  Rice distribution
  In probability theory, the Rice distribution or Rician distribution is the probability distribution of the absolute value of a circular bivariate normal random variable with potentially non-zero mean. It was named after Stephen O...
  
  
• The type-2 Gumbel distribution
• The Weibull distribution or Rosin Rammler distribution, of which the exponential distribution
  Exponential distribution
  In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
  
   is a special case, is used to model the lifetime of technical devices and is used to describe the particle size distribution
  Particle size distribution
  The particle-size distribution of a powder, or granular material, or particles dispersed in fluid, is a list of values or a mathematical function that defines the relative amounts of particles present, sorted according to size...
  
   of particles generated by grinding, milling
  Mill (grinding)
  A grinding mill is a unit operation designed to break a solid material into smaller pieces. There are many different types of grinding mills and many types of materials processed in them. Historically mills were powered by hand , working animal , wind or water...
  
   and crushing
  Crusher
  A crusher is a machine designed to reduce large rocks into smaller rocks, gravel, or rock dust. Crushers may be used to reduce the size, or change the form, of waste materials so they can be more easily disposed of or recycled, or to reduce the size of a solid mix of raw materials , so that pieces...
  
   operations.

Supported on the whole real line

• The Cauchy distribution
  Cauchy distribution
  The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
  
  , an example of a distribution which does not have an expected value
  Expected value
  In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
  
   or a variance
  Variance
  In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
  
  . In physics it is usually called a Lorentzian profile, and is associated with many processes, including resonance
  Resonance
  In physics, resonance is the tendency of a system to oscillate at a greater amplitude at some frequencies than at others. These are known as the system's resonant frequencies...
  
   energy distribution, impact and natural spectral line
  Spectral line
  A spectral line is a dark or bright line in an otherwise uniform and continuous spectrum, resulting from a deficiency or excess of photons in a narrow frequency range, compared with the nearby frequencies.- Types of line spectra :...
  
   broadening and quadratic stark
  Stark effect
  The Stark effect is the shifting and splitting of spectral lines of atoms and molecules due to presence of an external static electric field. The amount of splitting and or shifting is called the Stark splitting or Stark shift. In general one distinguishes first- and second-order Stark effects...
  
   line broadening.
• Chernoff's distribution
  Chernoff's distribution
  In probability theory, Chernoff's distribution, named after Herman Chernoff, is the probability distribution of the random variablewhere W is a "two-sided" Wiener process satisfying W = 0.If...
  
  
• The Fisher-Tippett, extreme value, or log-Weibull distribution
  • The Gumbel distribution, a special case of the Fisher-Tippett distribution
• Fisher's z-distribution
• The generalized logistic distribution
  Generalized logistic distribution
  The term generalized logistic distribution is used as the name for several different families of probability distributions. For example, Johnson et al. list four forms, which are listed below. One family described here has also been called the skew-logistic distribution...
  
  
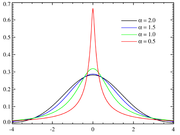
• The generalized normal distribution
• The geometric stable distribution
• The Holtsmark distribution
  Holtsmark distribution
  The Holtsmark distribution is a continuous probability distribution. The Holtsmark distribution is a special case of a stable distribution with the index of stability or shape parameter \alpha equal to 3/2 and skewness parameter \beta of zero. Since \beta equals zero, the distribution is...
  
  , an example of a distribution that has a finite expected value but infinite variance.
• The hyperbolic distribution
  Hyperbolic distribution
  The hyperbolic distribution is a continuous probability distribution that is characterized by the fact that the logarithm of the probability density function is a hyperbola. Thus the distribution decreases exponentially, which is more slowly than the normal distribution...
  
  
• The hyperbolic secant distribution
• The Landau distribution
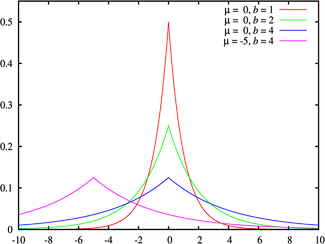
• The Laplace distribution
• The Lévy skew alpha-stable distribution or stable distribution is a family of distributions often used to characterize financial data and critical behavior; the Cauchy distribution
  Cauchy distribution
  The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
  
  , Holtsmark distribution
  Holtsmark distribution
  The Holtsmark distribution is a continuous probability distribution. The Holtsmark distribution is a special case of a stable distribution with the index of stability or shape parameter \alpha equal to 3/2 and skewness parameter \beta of zero. Since \beta equals zero, the distribution is...
  
  , Landau distribution, Lévy distribution and normal distribution are special cases.
• The Linnik distribution
• The logistic distribution
• The map-Airy distribution
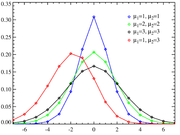
• The normal distribution, also called the Gaussian or the bell curve. It is ubiquitous in nature and statistics due to the central limit theorem
  Central limit theorem
  In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
  
  : every variable that can be modelled as a sum of many small independent, identically distributed variables with finite mean
  Mean
  In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
  
   and variance
  Variance
  In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
  
   is approximately normal.
• The Normal-exponential-gamma distribution
  Normal-exponential-gamma distribution
  In probability theory and statistics, the normal-exponential-gamma distribution is a three-parameter family of continuous probability distributions...
  
  
• The Pearson Type IV distribution (see Pearson distribution
  Pearson distribution
  The Pearson distribution is a family of continuous probability distributions. It was first published by Karl Pearson in 1895 and subsequently extended by him in 1901 and 1916 in a series of articles on biostatistics.- History :...
  
  s)
• The skew normal distribution
• Student's t-distribution, useful for estimating unknown means of Gaussian populations.
  • The noncentral t-distribution
    Noncentral t-distribution
    In probability and statistics, the noncentral t-distribution generalizes Student's t-distribution using a noncentrality parameter. Like the central t-distribution, the noncentral t-distribution is primarily used in statistical inference, although it may also be used in robust modeling for data...
    
    
• The type-1 Gumbel distribution
• The Voigt distribution, or Voigt profile, is the convolution of a normal distribution and a Cauchy distribution
  Cauchy distribution
  The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
  
  . It is found in spectroscopy when spectral line
  Spectral line
  A spectral line is a dark or bright line in an otherwise uniform and continuous spectrum, resulting from a deficiency or excess of photons in a narrow frequency range, compared with the nearby frequencies.- Types of line spectra :...
  
   profiles are broadened by a mixture of Lorentzian and Doppler
  Doppler broadening
  In atomic physics, Doppler broadening is the broadening of spectral lines due to the Doppler effect caused by a distribution of velocities of atoms or molecules. Different velocities of the emitting particles result in different shifts, the cumulative effect of which is the line broadening.The...
  
   broadening mechanisms.
• The Gaussian minus exponential distribution is a convolution of a normal distribution with (minus) an exponential distribution
  Exponential distribution
  In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
  
  .

With variable support

• The generalized extreme value distribution has a finite upper bound or a finite lower bound depending on what range the value of one of the parameters of the distribution is in (or is supported on the whole real line for one special value of the parameter
• The generalized Pareto distribution has a support which is either bounded below only, or bounded both above and below
• The Tukey lambda distribution is either supprted on the whole real line, or on a bounded interval, depending on what range the value of one of the parameters of the distribution is in.

Mixed discrete/continuous distributions

• The rectified Gaussian distribution
  Rectified Gaussian Distribution
  In probability theory, the rectified Gaussian distribution is a modification of the Gaussian distribution when its negative elements are reset to 0...
  
   replaces negative values from a normal distribution with a discrete component at zero.

Joint distributions

Two or more random variables on the same sample space

• The Dirichlet distribution, a generalization of the beta distribution.
• The Ewens's sampling formula
  Ewens's sampling formula
  In population genetics, Ewens' sampling formula, describes the probabilities associated with counts of how many different alleles are observed a given number of times in the sample.-Definition:...
  
   is a probability distribution on the set of all partitions of an integer n, arising in population genetics
  Population genetics
  Population genetics is the study of allele frequency distribution and change under the influence of the four main evolutionary processes: natural selection, genetic drift, mutation and gene flow. It also takes into account the factors of recombination, population subdivision and population...
  
  .
• The Balding–Nichols model
• The multinomial distribution, a generalization of the binomial distribution.
• The multivariate normal distribution, a generalization of the normal distribution.
• The negative multinomial distribution, a generalization of the negative binomial distribution
  Negative binomial distribution
  In probability theory and statistics, the negative binomial distribution is a discrete probability distribution of the number of successes in a sequence of Bernoulli trials before a specified number of failures occur...
  
  .

Matrix-valued distributions

• The Wishart distribution
• The inverse-Wishart distribution
• The matrix normal distribution
  Matrix normal distribution
  The matrix normal distribution is a probability distribution that is a generalization of the normal distribution to matrix-valued random variables.- Definition :...
  
  
• The matrix t-distribution

Miscellaneous distributions

• The Cantor distribution
• The phase-type distribution
  Phase-type distribution
  A phase-type distribution is a probability distribution that results from a system of one or more inter-related Poisson processes occurring in sequence, or phases. The sequence in which each of the phases occur may itself be a stochastic process. The distribution can be represented by a random...
  
  
• The truncated distribution
  Truncated distribution
  In statistics, a truncated distribution is a conditional distribution that results from restricting the domain of some other probability distribution. Truncated distributions arise in practical statistics in cases where the ability to record, or even to know about, occurrences is limited to values...
  
  
• The mixture distribution

See also

• Copula (statistics)
  Copula (statistics)
  In probability theory and statistics, a copula can be used to describe the dependence between random variables. Copulas derive their name from linguistics....
  
  
• Cumulative distribution function
  Cumulative distribution function
  In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
  
  
• Likelihood function
  Likelihood function
  In statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
  
  
• List of statistical topics
• Probability density function
  Probability density function
  In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
  
  
• Random variable
  Random variable
  In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
  
  
• Histogram
  Histogram
  In statistics, a histogram is a graphical representation showing a visual impression of the distribution of data. It is an estimate of the probability distribution of a continuous variable and was first introduced by Karl Pearson...
  
  
• Truncated distribution
  Truncated distribution
  In statistics, a truncated distribution is a conditional distribution that results from restricting the domain of some other probability distribution. Truncated distributions arise in practical statistics in cases where the ability to record, or even to know about, occurrences is limited to values...
  
  
• Probability distribution
  Probability distribution
  In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....