
Statistical independence
Encyclopedia
In probability theory
, to say that two event
s are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs. For example:
Similarly, two random variable
s are independent if the conditional probability distribution of either given the observed value of the other is the same as if the other's value had not been observed. The concept of independence extends to dealing with collections of more than two events or random variables.
In some instances, the term "independent" is replaced by "statistically independent", "marginally independent", or "absolutely independent".
Here A ∩ B is the intersection
of A and B, that is, it is the event that both events A and B occur.
More generally, any collection of events—possibly more than just two of them—are mutually independent if and only if for every finite subset A1, ..., An of the collection we have

This is called the multiplication rule for independent events. Notice that independence requires this rule to hold for every subset of the collection; see for a three-event example in which and yet no two of the three events are pairwise independent.
and yet no two of the three events are pairwise independent.
If two events A and B are independent, then the conditional probability
of A given B is the same as the unconditional (or marginal) probability of A, that is,
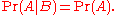
There are at least two reasons why this statement is not taken to be the definition of independence: (1) the two events A and B do not play symmetrical roles in this statement, and (2) problems arise with this statement when events of probability 0 are involved.
The conditional probability of event A given B is given by
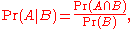 (so long as Pr(B) ≠ 0 )
(so long as Pr(B) ≠ 0 )
The statement above, when is equivalent to
is equivalent to

which is the standard definition given above.
Note that an event is independent of itself if and only if
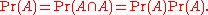
That is, if its probability is one or zero. Thus if an event or its complement
almost surely
occurs, it is independent of itself. For example, if event A is choosing any number but 0.5 from a uniform distribution
on the unit interval
, A is independent of itself, even though, tautologically
, A fully determines A.
s. If X is a real
-valued random variable and a is a number then the event X ≤ a is the set of outcomes whose corresponding value of X is less than or equal to a. Since these are sets of outcomes that have probabilities, it makes sense to refer to events of this sort being independent of other events of this sort.
Two random variables X and Y are independent if and only if
for every a and b, the events {X ≤ a} and {Y ≤ b} are independent events as defined above. Mathematically, this can be described as follows:
The random variables X and Y with cumulative distribution function
s FX(x) and FY(y), and probability densities
ƒX(x) and ƒY(y), are independent if and only if the combined random variable (X, Y) has a joint
cumulative distribution function
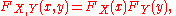
or equivalently, a joint density
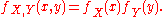 .
.
Similar expressions characterise independence more generally for more than two random variables.
An arbitrary collection of random variables – possibly more than just two of them — is independent precisely if for any finite collection X1, ..., Xn and any finite set of numbers a1, ..., an, the events {X1 ≤ a1}, ..., {Xn ≤ an} are independent events as defined above.
The measure-theoretically inclined may prefer to substitute events {X ∈ A} for events {X ≤ a} in the above definition, where A is any Borel set
. That definition is exactly equivalent to the one above when the values of the random variables are real number
s. It has the advantage of working also for complex-valued random variables or for random variables taking values in any measurable space (which includes topological space
s endowed by appropriate σ-algebras).
If any two of a collection of random variables are independent, they may nonetheless fail to be mutually independent; this is called pairwise independence
.
If X and Y are independent, then the expectation operator
E has the property

and for the covariance
since we have
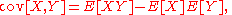
so the covariance
cov(X, Y) is zero.
(The converse of these, i.e. the proposition that if two random variables have a covariance of 0 they must be independent, is not true. See uncorrelated
.)
Two independent random variables X and Y have the property that the characteristic function
of their sum is the product of their marginal characteristic functions:

but the reverse implication is not true (see subindependence).
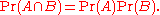
The new definition relates to the previous ones very directly:
Using this definition, it is easy to show that if X and Y are random variables and Y is constant, then X and Y are independent, since the σ-algebra generated by a constant random variable is the trivial σ-algebra {∅, Ω}.
Probability zero events cannot affect independence so independence also holds if Y is only Pr-almost surely
constant.
The formal definition of conditional independence is based on the idea of conditional distribution
s. If X, Y, and Z are discrete random variables, then we define X and Y to be conditionally independent given Z if

for all x, y and z such that P(Z = z) > 0. On the other hand, if the random variables are continuous and have a joint probability density function
p, then X and Y are conditionally independent given Z if
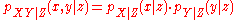
for all real numbers x, y and z such that pZ(z) > 0.
If X and Y are conditionally independent given Z, then
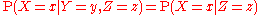
for any x, y and z with P(Z = z) > 0. That is, the conditional distribution for X given Y and Z is the same as that given Z alone. A similar equation holds for the conditional probability density functions in the continuous case.
Independence can be seen as a special kind of conditional independence, since probability can be seen as a kind of conditional probability given no events.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, to say that two event
Event (probability theory)
In probability theory, an event is a set of outcomes to which a probability is assigned. Typically, when the sample space is finite, any subset of the sample space is an event...
s are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs. For example:
- The event of getting a 6 the first time a die is rolled and the event of getting a 6 the second time are independent.
- By contrast, the event of getting a 6 the first time a die is rolled and the event that the sum of the numbers seen on the first and second trials is 8 are not independent.
- If two cards are drawn with replacement from a deck of cards, the event of drawing a red card on the first trial and that of drawing a red card on the second trial are independent.
- By contrast, if two cards are drawn without replacement from a deck of cards, the event of drawing a red card on the first trial and that of drawing a red card on the second trial are again not independent.
Similarly, two random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s are independent if the conditional probability distribution of either given the observed value of the other is the same as if the other's value had not been observed. The concept of independence extends to dealing with collections of more than two events or random variables.
In some instances, the term "independent" is replaced by "statistically independent", "marginally independent", or "absolutely independent".
Independent events
The standard definition says:- Two events A and B are independent if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
Pr(A ∩ B) = Pr(A)Pr(B).
Here A ∩ B is the intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of A and B, that is, it is the event that both events A and B occur.
More generally, any collection of events—possibly more than just two of them—are mutually independent if and only if for every finite subset A1, ..., An of the collection we have

This is called the multiplication rule for independent events. Notice that independence requires this rule to hold for every subset of the collection; see for a three-event example in which
 and yet no two of the three events are pairwise independent.
and yet no two of the three events are pairwise independent.If two events A and B are independent, then the conditional probability
Conditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
of A given B is the same as the unconditional (or marginal) probability of A, that is,
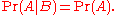
There are at least two reasons why this statement is not taken to be the definition of independence: (1) the two events A and B do not play symmetrical roles in this statement, and (2) problems arise with this statement when events of probability 0 are involved.
The conditional probability of event A given B is given by
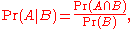 (so long as Pr(B) ≠ 0 )
(so long as Pr(B) ≠ 0 )The statement above, when
 is equivalent to
is equivalent to
which is the standard definition given above.
Note that an event is independent of itself if and only if
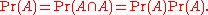
That is, if its probability is one or zero. Thus if an event or its complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
almost surely
Almost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
occurs, it is independent of itself. For example, if event A is choosing any number but 0.5 from a uniform distribution
Uniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
on the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
, A is independent of itself, even though, tautologically
Tautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
, A fully determines A.
Independent random variables
What is defined above is independence of events. In this section we treat independence of random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s. If X is a real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
-valued random variable and a is a number then the event X ≤ a is the set of outcomes whose corresponding value of X is less than or equal to a. Since these are sets of outcomes that have probabilities, it makes sense to refer to events of this sort being independent of other events of this sort.
Two random variables X and Y are independent if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
for every a and b, the events {X ≤ a} and {Y ≤ b} are independent events as defined above. Mathematically, this can be described as follows:
The random variables X and Y with cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
s FX(x) and FY(y), and probability densities
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
ƒX(x) and ƒY(y), are independent if and only if the combined random variable (X, Y) has a joint
Joint distribution
In the study of probability, given two random variables X and Y that are defined on the same probability space, the joint distribution for X and Y defines the probability of events defined in terms of both X and Y...
cumulative distribution function
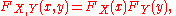
or equivalently, a joint density
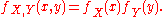 .
.Similar expressions characterise independence more generally for more than two random variables.
An arbitrary collection of random variables – possibly more than just two of them — is independent precisely if for any finite collection X1, ..., Xn and any finite set of numbers a1, ..., an, the events {X1 ≤ a1}, ..., {Xn ≤ an} are independent events as defined above.
The measure-theoretically inclined may prefer to substitute events {X ∈ A} for events {X ≤ a} in the above definition, where A is any Borel set
Borel algebra
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
. That definition is exactly equivalent to the one above when the values of the random variables are real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. It has the advantage of working also for complex-valued random variables or for random variables taking values in any measurable space (which includes topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s endowed by appropriate σ-algebras).
If any two of a collection of random variables are independent, they may nonetheless fail to be mutually independent; this is called pairwise independence
Pairwise independence
In probability theory, a pairwise independent collection of random variables is a set of random variables any two of which are independent. Any collection of mutually independent random variables is pairwise independent, but some pairwise independent collections are not mutually independent...
.
If X and Y are independent, then the expectation operator
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
E has the property

and for the covariance
Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
since we have
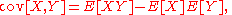
so the covariance
Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
cov(X, Y) is zero.
(The converse of these, i.e. the proposition that if two random variables have a covariance of 0 they must be independent, is not true. See uncorrelated
Uncorrelated
In probability theory and statistics, two real-valued random variables are said to be uncorrelated if their covariance is zero. Uncorrelatedness is by definition pairwise; i.e...
.)
Two independent random variables X and Y have the property that the characteristic function
Characteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
of their sum is the product of their marginal characteristic functions:

but the reverse implication is not true (see subindependence).
Independent σ-algebras
The definitions above are both generalized by the following definition of independence for σ-algebras. Let (Ω, Σ, Pr) be a probability space and let A and B be two sub-σ-algebras of Σ. A and B are said to be independent if, whenever A ∈ A and B ∈ B,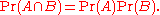
The new definition relates to the previous ones very directly:
- Two events are independent (in the old sense) if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the σ-algebras that they generate are independent (in the new sense). The σ-algebra generated by an event E ∈ Σ is, by definition,
-
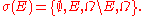
- Two random variables X and Y defined over Ω are independent (in the old sense) if and only if the σ-algebras that they generate are independent (in the new sense). The σ-algebra generated by a random variable X taking values in some measurable space S consists, by definition, of all subsets of Ω of the form X−1(U), where U is any measurable subset of S.
Using this definition, it is easy to show that if X and Y are random variables and Y is constant, then X and Y are independent, since the σ-algebra generated by a constant random variable is the trivial σ-algebra {∅, Ω}.
Probability zero events cannot affect independence so independence also holds if Y is only Pr-almost surely
Almost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
constant.
Conditionally independent random variables
Intuitively, two random variables X and Y are conditionally independent given Z if, once Z is known, the value of Y does not add any additional information about X. For instance, two measurements X and Y of the same underlying quantity Z are not independent, but they are conditionally independent given Z (unless the errors in the two measurements are somehow connected).The formal definition of conditional independence is based on the idea of conditional distribution
Conditional distribution
Given two jointly distributed random variables X and Y, the conditional probability distribution of Y given X is the probability distribution of Y when X is known to be a particular value...
s. If X, Y, and Z are discrete random variables, then we define X and Y to be conditionally independent given Z if

for all x, y and z such that P(Z = z) > 0. On the other hand, if the random variables are continuous and have a joint probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
p, then X and Y are conditionally independent given Z if
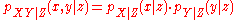
for all real numbers x, y and z such that pZ(z) > 0.
If X and Y are conditionally independent given Z, then
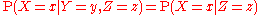
for any x, y and z with P(Z = z) > 0. That is, the conditional distribution for X given Y and Z is the same as that given Z alone. A similar equation holds for the conditional probability density functions in the continuous case.
Independence can be seen as a special kind of conditional independence, since probability can be seen as a kind of conditional probability given no events.
See also
- Copula (statistics)Copula (statistics)In probability theory and statistics, a copula can be used to describe the dependence between random variables. Copulas derive their name from linguistics....
- Independent and identically distributed random variablesIndependent and identically distributed random variablesIn probability theory and statistics, a sequence or other collection of random variables is independent and identically distributed if each random variable has the same probability distribution as the others and all are mutually independent....
- Mutually exclusive events
- Subindependence
- Linear dependence between random variables
- Conditional independenceConditional independenceIn probability theory, two events R and B are conditionally independent given a third event Y precisely if the occurrence or non-occurrence of R and the occurrence or non-occurrence of B are independent events in their conditional probability distribution given Y...

