
Rectified Gaussian Distribution
Encyclopedia
In probability theory
, the rectified Gaussian distribution is a modification of the Gaussian distribution when its negative elements are reset to 0. It is essentially a mixture of a discrete distribution (constant 0) and a continuous distribution (a truncated
Gaussian distribution with interval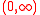 ).
).
of a rectified Gaussian distribution, for which random variable
s X having this distribution are displayed as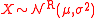 , is given by
, is given by
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, the rectified Gaussian distribution is a modification of the Gaussian distribution when its negative elements are reset to 0. It is essentially a mixture of a discrete distribution (constant 0) and a continuous distribution (a truncated
Truncated distribution
In statistics, a truncated distribution is a conditional distribution that results from restricting the domain of some other probability distribution. Truncated distributions arise in practical statistics in cases where the ability to record, or even to know about, occurrences is limited to values...
Gaussian distribution with interval
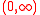 ).
).Density function
The probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of a rectified Gaussian distribution, for which random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s X having this distribution are displayed as
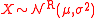 , is given by
, is given by
-
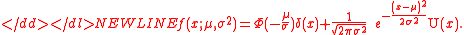
Here,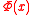 is the cumulative distribution functionCumulative distribution functionIn probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
is the cumulative distribution functionCumulative distribution functionIn probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
(cdf) of the standard normal distribution:-

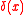 is the Dirac delta functionDirac delta functionThe Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
is the Dirac delta functionDirac delta functionThe Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
and,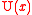 is the unit step function:
is the unit step function: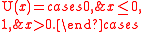
Alternative form
Often, a simpler alternative form is to consider a case, where,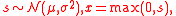
then,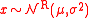
Application
A rectified Gaussian distribution is conjugate to the Gaussian likelihood, and it has been recently applied to factor analysisFactor analysisFactor analysis is a statistical method used to describe variability among observed, correlated variables in terms of a potentially lower number of unobserved, uncorrelated variables called factors. In other words, it is possible, for example, that variations in three or four observed variables...
, or particularly, (non-negative) rectified factor analysis.
Harva proposed a variational learning algorithm for the rectified factor model, where the factors follow a mixture of rectified Gaussian; and later Meng proposed an infinite rectified factor model coupled with its Gibbs sampling solution, where the factors follow a Dirichlet processDirichlet processIn probability theory, a Dirichlet process is a stochastic process that can be thought of as a probability distribution whose domain is itself a random distribution...
mixture of rectified Gaussian distribution, and applied it in computational biology for reconstruction of gene regulatory network. -
-


